Multi

7.1n-step TD Prediction

The methods that usen-step backups are still TD methodsbecause theystill change an earlier estimate based on how it differs from a later estimate.

n-step return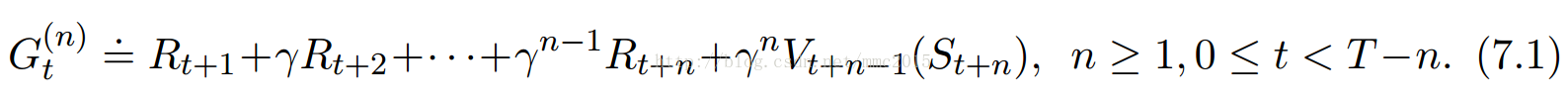：If t+n≥T(if then-step return extends to or beyond termination), then all the missing terms are taken as zero

==》这个很容易理解，最后n步之内，还剩多少步就令return等于所有剩余步数的reward和。相应的，前n-1步也是没有任何更新过程，Note that no changes at all are made during the firstn-1 steps of each episode.。n-step return的error往往更小：Methods that involve an intermediate amount of bootstrapping are important because they will typically perform better than either extreme.

7.2 n-step SARSA

将V改成Q即可，整个流程基本一致：

想一下为什么n-step的方法能更有效地更新Q-table：因为每一个好的(s,a)或坏的(s,a)在更新过程中都会被使用n次（看上面伪代码），这样可以有效的backup到n-step之前的相关(s,a)。

7.3n-step Off-policy Learning by Importance Sampling

The importance sampling that we have used in this section and in Chapter 5 enables off-policy learning, but at the cost of increasing the variance of the updates. The high variance forces us to use a small step-size parameter, resulting in slow learning. It is probably inevitable that off-policy training is slower than on-policy training|after all, the data is less relevant to what you are trying to learn.

7.4 Off-policy Learning Without Importance Sampling: Then-step Tree Backup Algorithm

7.3/7.4在实际中很少用吧，跳过去了。其中12章的eligibility traces应该是n-step方法部分应该掌握的重点。

silver课程的lecture 4中30页之后的内容、lecture 5中26-30页关于n-step algorithm以及eligibility trace的介绍非常简单明了。

forward-view TD(λ)：

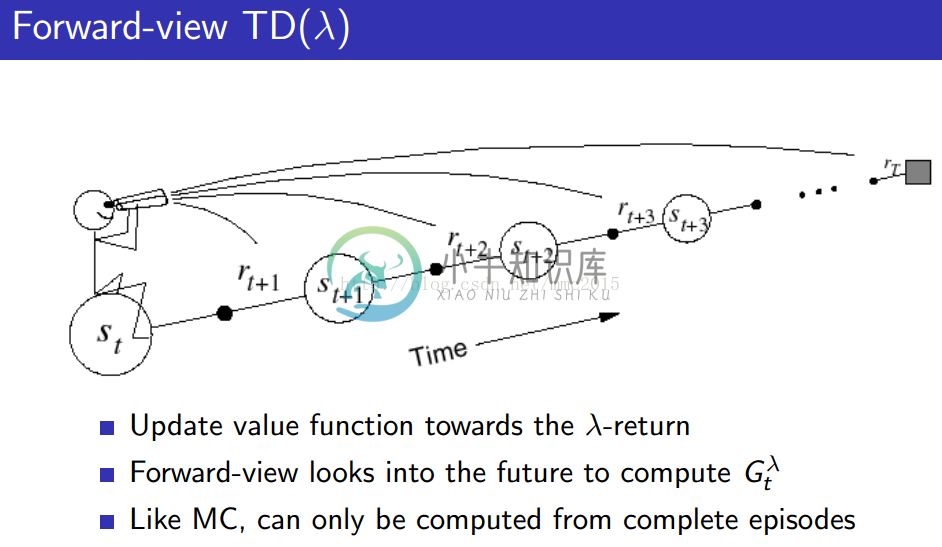
backward-view TD(λ)：

Forward view provides theory
Backward view provides mechanism
Update online, every step, from incomplete sequences

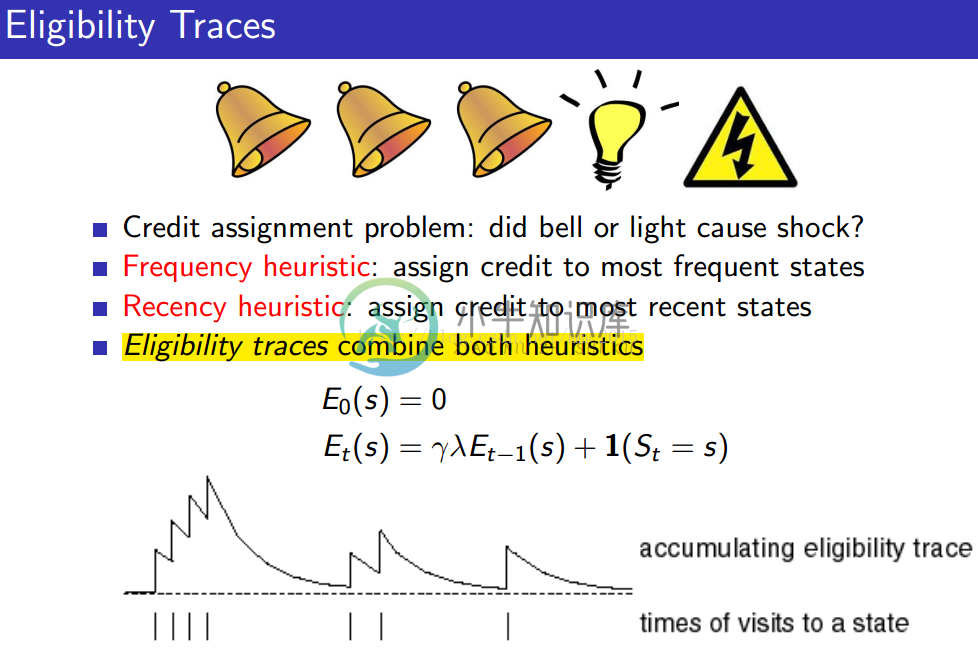
λ=0，TD(λ)就是之前提到的TD(0)方法；λ=1，forward-view TD(λ)就是之前提到的MC方法，backward-view 的online TD(λ)近似是之前提到的MC方法。

forward-view SARSA(λ)：

backward-view SARSA(λ)：