Q

Q-Learning 决策

假设我们的行为准则已经学习好了, 现在我们处于状态s1, 我在写作业, 我有两个行为 a1, a2, 分别是看电视和写作业, 根据我的经验, 在这种 s1 状态下, a2 写作业 带来的潜在奖励要比 a1 看电视高, 这里的潜在奖励我们可以用一个有关于 s 和 a 的 Q 表格代替, 在我的记忆Q表格中, Q(s1, a1)=-2 要小于 Q(s1, a2)=1, 所以我们判断要选择 a2 作为下一个行为. 现在我们的状态更新成 s2 , 我们还是有两个同样的选择, 重复上面的过程, 在行为准则Q 表中寻找 Q(s2, a1) Q(s2, a2) 的值, 并比较他们的大小, 选取较大的一个. 接着根据 a2 我们到达 s3 并在此重复上面的决策过程. Q learning 的方法也就是这样决策的. 看完决策, 我看在来研究一下这张行为准则 Q 表是通过什么样的方式更改, 提升的.

Q-Learning 更新

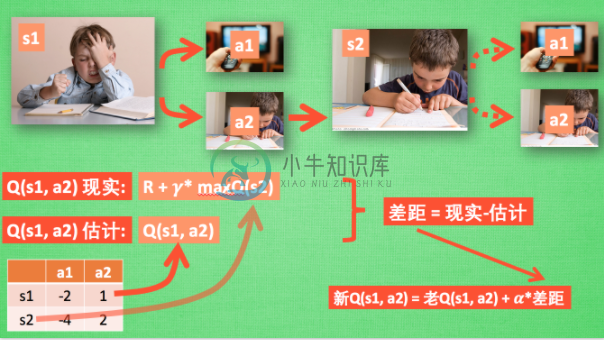
所以我们回到之前的流程, 根据 Q 表的估计, 因为在 s1 中, a2 的值比较大, 通过之前的决策方法, 我们在 s1 采取了 a2, 并到达 s2, 这时我们开始更新用于决策的 Q 表, 接着我们并没有在实际中采取任何行为, 而是再想象自己在 s2 上采取了每种行为, 分别看看两种行为哪一个的 Q 值大, 比如说 Q(s2, a2) 的值比 Q(s2, a1) 的大, 所以我们把大的 Q(s2, a2) 乘上一个衰减值 gamma (比如是0.9) 并加上到达s2时所获取的奖励 R (这里还没有获取到我们的棒棒糖, 所以奖励为 0), 因为会获取实实在在的奖励 R , 我们将这个作为我现实中 Q(s1, a2) 的值, 但是我们之前是根据 Q 表估计 Q(s1, a2) 的值. 所以有了现实和估计值, 我们就能更新Q(s1, a2) , 根据 估计与现实的差距, 将这个差距乘以一个学习效率 alpha 累加上老的 Q(s1, a2) 的值 变成新的值. 但时刻记住, 我们虽然用 maxQ(s2) 估算了一下 s2 状态, 但还没有在 s2 做出任何的行为, s2 的行为决策要等到更新完了以后再重新另外做. 这就是 off-policy 的 Q learning 是如何决策和学习优化决策的过程.

Q-Learning 整体算法

这一张图概括了我们之前所有的内容. 这也是 Q learning 的算法, 每次更新我们都用到了 Q 现实和 Q 估计, 而且 Q learning 的迷人之处就是 在 Q(s1, a2) 现实 中, 也包含了一个 Q(s2) 的最大估计值, 将对下一步的衰减的最大估计和当前所得到的奖励当成这一步的现实, 很奇妙吧. 最后我们来说说这套算法中一些参数的意义. Epsilon greedy 是用在决策上的一种策略, 比如 epsilon = 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为. alpha是学习率, 来决定这次的误差有多少是要被学习的, alpha是一个小于1 的数. gamma 是对未来 reward 的衰减值. 我们可以这样想象.

我们重写一下 Q(s1) 的公式, 将 Q(s2) 拆开, 因为Q(s2)可以像 Q(s1)一样,是关于Q(s3) 的, 所以可以写成这样, 然后以此类推, 不停地这样写下去, 最后就能写成这样, 可以看出Q(s1) 是有关于之后所有的奖励, 但这些奖励正在衰减, 离 s1 越远的状态衰减越严重. 不好理解? 行, 我们想象 Qlearning 的机器人天生近视眼, gamma = 1 时, 机器人有了一副合适的眼镜, 在 s1 看到的 Q 是未来没有任何衰变的奖励, 也就是机器人能清清楚楚地看到之后所有步的全部价值, 但是当 gamma =0, 近视机器人没了眼镜, 只能摸到眼前的 reward, 同样也就只在乎最近的大奖励, 如果 gamma 从 0 变到 1, 眼镜的度数由浅变深, 对远处的价值看得越清楚, 所以机器人渐渐变得有远见, 不仅仅只看眼前的利益, 也为自己的未来着想.