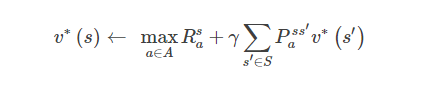动态编程
1. Introduction:DP(Dynamic Programming)
定义
- 解决复杂问题的一种方法。将多阶过程分解为一些列单阶段问题,逐个求解,最后结合起来以解决这类过程优化问题。
- 同时,将这些子问题的解保存起来,如果下一次遇到了相同的子问题,则不需要重新计算子问题的解。
DP主要用于解决含有以下两点特性的问题
- 最优子结构:最优解能被分解为子问题,最优应用原则
- 覆盖子问题:子问题多次出现,子问题的解可以被缓存和重复利用
MDPs满足上述两条性质
- 贝尔曼等式给出递归分解形式,可以切分成子问题。
- 值函数存储和重复利用可行解,即保存了子问题的解**=>**可以通过DP求解MDPs
应用:用于MDP中的决策问题
针对MDP,切分的子问题就是在每个状态下应该选择哪个action。同时,这一时刻的子问题取决于上一时刻的子问题选择了哪个action。
注意:当已知MDPs的状态转移矩阵时,环境模型就已知了,此时可看为planning问题。
2. Policy Evaluation
基于当前的policy计算出每个状态的value function。
Iterative Policy Evaluation,策略迭代估计
- 问题:评估一个给定的策略
- 解决方法:迭代,贝尔曼期望备份, v1→v2→⋯→vπ
- 采用同步备份
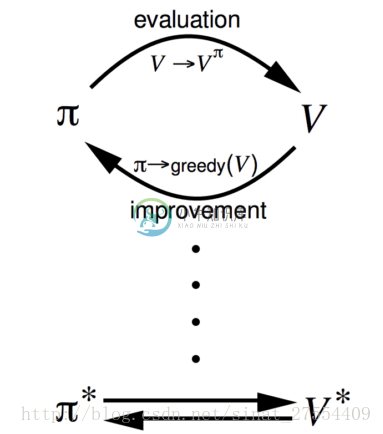
3. Policy Iteration
解决过程分为2步
policy evaluation
基于当前的policy计算每个状态的value functionPolicy Improvement
基于当前的value function,采用贪心算法来找到当前最优秀的policy
eg: Given a policyπ
evaluate the policy π:vπ(s)=E[Rt+1+γRt+2+⋯|St=s]
improve the policy by acting greedy with respect to vπ:π′=greedy(vπ)
注意:该策略略迭代过程总是会收敛到最优策略π∗。
4. Value Iteration
Value Iteration in MDPs
最优化原理:当且仅当任何从状态s能达到的状态s’都能在当前状态下取得最优的value时,那么状态s也能在当前的policy下获得最优的value。即vπ(s)=v∗(s)。任何最优策略都可以被细分为两部分:
- 最优的第一个action A∗
- 接下来后续状态s’下的最优策略
Deterministic Value Iteration
如果已知子问题的最优解v∗(s′),则可以通过第一个Bellman Optimality Equation将v∗(s)也求出来,因此从终点向起点推导就可以推出所有的状态最优值。
Value Iteration通过迭代的方法,通过这一步的vk(s′)更新下一步的vk+1(s),不断迭代,最终收敛到最优的v∗。
*注意:中间生成的value function不对应任何policy。
Policy Iteration和Value Iteration有什么本质区别?为什么一个叫policy iteration,一个叫value iteration呢?
- 原因其实很好理解,policy iteration使用bellman方程来更新value,最后收敛的value 即vπ是当前policy下的value值(所以叫做对policy进行评估),目的是为了后面的policy improvement得到新的policy。
- 而value iteration是使用bellman 最优方程来更新value,最后收敛得到的value即v∗就是当前state状态下的最优的value值。因此,只要最后收敛,那么最优的policy也就得到的。因此这个方法是基于更新value的,所以叫value iteration。
- 从上面的分析看,value iteration较之policy iteration更直接。不过问题也都是一样,需要知道状态转移函数p才能计算。本质上依赖于模型,而且理想条件下需要遍历所有的状态,这在稍微复杂一点的问题上就基本不可能了。
针对MDPs要解决的2个问题,有如下解决办法:
- 针对prediction 目标是在已知policy下得到收敛的value function,因此针对问题不断迭代计算Bellman Expectation Equation就足够了。
- 针对control 需要同时获得最优的policy,那么在Iterative policy evaluation基础上加入一个选择policy的过程就行。此外,通过value iteration在得到最优的value function后推导出最优policy。
整理:
问题 贝尔曼方程 解决算法 Prediction Bellman Expectation Equation Iterative Policy Evaluation Control Bellman Expectation Equation & Greedy Policy Improvement Policy Iteration Control Bellman Optimality Equation Value Iteration 5. DP的一些扩展
- Asynchronous Dynamics Programming 异步动态规划 那么上面的算法的核心是更新每个状态的value值。那么可以通过运行多个实例同时采集样本来实现异步更新。而基于异步更新的思想,DeepMind出了一篇不错的paper:Asynchronous Methods for Deep Reinforcement Learning该文对于Atari游戏的效果得到大幅提升。
- Full-Width Backups &Sample Backups
- Approximate DP
6. Contraction Mapping 压缩映射
压缩映射定理为本节的主要数学依据,解释了为何value iteration收敛于v∗,为何Policy Evaluation收敛于vπ,为何Policy Iteration收敛于v∗。