附录3：关于各态历经信源的定理

如果有可能沿一条概率为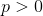的路径，由任意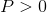的状态转入任意其他状态，则该系统是各态历经的，可以适用严格的大数定律。因此，该网络中一条给定路径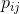在一条长度为N的长序列中的遍历次数正比于它在i处、然后选择这一路径的概率（比如说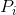），即。如果N足够大，使出现百分比误差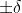的概率小于，使得除一个小概率集合之外，其他所有实际数值都位于下面的界限内：

。

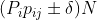因此，几乎所有序列的概率均为p，给出如下：

而的范围为：

或

。

这就证明了定理3。

根据定理3中p值的可能范围，计算n(q)的上下限，立刻就可以推出定理4。

在混合（非各态历经）情景中，如果

各个分量的熵为，我们有：

定理： 是递减阶梯函数，

在区间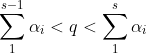中，有。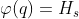

为了证明定理5和6，首先注意到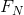是单调递减的，因为增大N值会向条件熵增加一个下标。将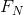的定义中对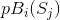进行简单的代入，可以证明：

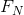
并针对所有N值进行求和，得出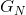。因此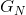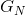，，为单调递减。它们也必然趋近于相同极限。利用定理3，可以看出。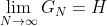