27. 保真度评价函数

对于一个离散信源，我们能够算出一个确定的信息生成速率，也就是其随机过程的熵。对于连续信源，情况就要复杂得多。首先，连续变化量可以取无数个值，需要无数个二进制数位才能准确表示。这意味着要将一个连续信源的输出传送到接收端，而且能够完全恢复，一般情况下需要有一个具有无穷大容量（单位为比特/秒）的信道。由于在一般情况下，信道中总会有一定数量的噪声，而且容量是有限的，所以不可能实现精确传送。

但这种说法模糊了真正的问题。实际上，对于连续信源，我们感兴趣的并不是精确传送，而是在特定容差范围内的传送。问题是，当我们仅需要特定的恢复保真度（采用适当的形式度量）时，能否为连续信源指定一个确定的生成速率。当然，随着保真度要求的增大，该速率会下降。可以证明，在非常一般的情况下，我们能够定义这样一个具有如下性质的速率：通过正确的信息编码，有可能通过一个容量等于该速率的信道来传送该信息，同时满足保真度要求。当信道容量更小时，则不足以正确传送该信息。

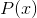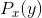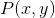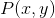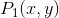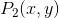首先，对于传输保真度的概念，需要给出一种一般性的数学描述。考虑一组持续时间很长的消息，比如为T秒。一个信源可以描述如下：给出该信源在相关空间内选择特定消息的概率密度。一个给定通信系统可以描述如下（从外部视角来看）：给出信源生成消息x而接收端恢复出消息y的条件概率。该系统作为一个整体（包括信源和传送系统），可以用发出消息x而最终输出为y的概率函数来描述。如果已知此函数，那么从保真度的角度来看，该系统的完整特性就是已知的。对保真度的任意评价在数学上必须对应于对应用的一种运算。这种运算至少要为这些系统建立一种简单的顺序关系；即，对于两个分别用和表示的系统，必须能够根据我们的保真度准则做出以下判定之一：(1)第一个系统的保真度较高，(2)第二个系统的保真度较高，或者(3)它们的保真度相同。这意味着保真度准则可以用一个数值函数表示：

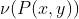
其参数的变化范围是所有可能存在的概率函数。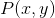

我们现在将证明，在非常一般且合理的假定条件下，函数可以写为一种非常专业的形式，即在x和y的取值范围内，对函数求均值：

为得到这一结果，只需要假定：(1)信源和系统是各态历经的，这样，一个非常长的样本成为该系集典型代表的概率接近于1，(2)该评价是“合理”的，也就是说，通过观察典型输入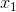和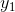，有可能基于这些样本给出一个尝试性评价；如果这些样本的持续时间增大，则这一尝试性评价将以概率1趋近于根据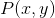的全部知识所获得的精确评价。设该尝试性评价为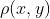。在与该系统相对应的高概率区域中的几乎所有(x,y)，当时，函数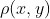趋近于一个常数：

另外，由于：

所以可写出：

这就给出了所要的结果。

函数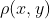具有x与y之间“距离”的一般特性。它衡量了在发送x，收到y时的意外程度（根据我们的保真度准则）。上面给出的一般性结果可以重新表述如下：只要使消息的持续时间T足够大，任何合理的评价都可以表示为一个距离函数的均值，这里所说的均值，是指根据发送消息x、接收消息y的概率，在x和y的集合上进行加权平均。

下面是几个简单的评价函数例子：

1. RMS准则。
   
   在这种很常用的保真度度量中，距离函数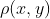就是相关联的函数空间中点x和点y之间普通欧氏距离的平方（只相当一个常数因子）。
   

2. 频率加权RMS准则。更一般的情况下，在应用保真度的RMS度量之前，可以对不同频率分量应用不同权值。这相当于将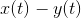通过一个赋形滤波器，以决定输出的平均功率。因此，设：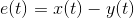
   
   及
   
   则
   

3. 绝对误差准则。
   

4. 耳朵和大脑的结构隐含了确定了一种评价或相当大量的评价，适用于语音或音乐传输的情况。例如，存在一种“可懂度”准则，在这一准则中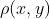，等于错误解读单词的频率，也就是发送消息x(t)，被接收为y(t)。尽管在这些情况下无法给出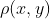的显式表示，则在原理上，可以通过足够多的试验确定这些情况。它的一些性质是从一些众所周知的听力试验结果中获得的，例如，耳朵对相位相对不够敏感，对振幅和频率的敏感度近似为对数特性。

5. 离散情景可以看作是一种特殊化，在此情况下，我们根据错误频率来假设评价准则。因此，函数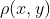定义为：序列y中的符号不同于x中相应符号的数目，除以x中的总符号数。