5. 各态历经与混合信源

上面已经指出，可以认为我们使用的离散信源能够用马尔可夫过程来表示。在各种可能存在的离散马尔可夫过程中，有一组过程拥有一些在通信理论中极为重要的特殊性质。这一特殊类别由“各态历经”过程组成，我们将相应的信源称为各态历经信源。尽管各态历经过程的严格定义有些复杂，但其一般思想却很简单。在各态历经过程中，该过程所生成的每个序列都具有相同的统计性质。 因此，由特定序列获得的字符频率、二连字频率等数值，将会随着这些序列长度的增加，趋近于与该特定序列无关的确切极限。实际上，这一点并非对于所有序列都成立，但是，使之不成立的序列集的出现概率为0。概略地来说，各态历经性意味着统计意义上的均匀性。

上面给出的所有虚拟语言示例都是各态历经的。这一性质与相应图中的结构相关联。如果图形具有以下两个性质，则相应的过程是各态历经的：

1. 图中不存在这样两个相互分离的A、B部分：根据箭头的方向，无法沿着图中的连线，由A部分的交点到达B部分中的交点，也无法由B部分的交点到达A部分的交点。

2. 如果图中有一系列连线闭合起来，而且连线上的所有箭头都指向相同方向，将这些闭合线称为“回路”。一个回路的“长度”就是其中连线的数目。因此，在图5中，BEBES是一个长度为5的回路。需要满足的第二个性质是，图中所有回路长度的最大公约数为1。

如果满足第一个条件，但不满足第二个条件，该最大公约数d大于1，则此类序列会拥有某种特定类型的周期结构。各个序列会被划分为d个不同类别，除了相对于原点的一个偏移之外，这些类别在统计意义上是相同的（这里所说的“原点”，是指序列中被称为“字符1”的那个字符）。任何一个序列，只要将其移动0到d - 1个位置，就可以使它与任意其他序列实现统计等价。下面是一个d = 2的简单示例：存在三个可能字符a, b, c。字符a后面跟有b或c的概率分别为和。b和c后面总是跟有字符a。因此，一个典型序列为：
a b a c a c a c a b a c a b a b a c a c
这种情景在我们的研究中并不是特别重要。

如果不满足第一个条件，则可以将图形划分为两个分别满足该第一条件的子图。我们将假定对于每个子图都满足第二个条件。在此情况下，将会得到由一些单纯分量组成的所谓“混合”信源。这些分量与各个子图相对应。如果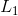为分量信源，则可以记作：

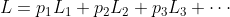
其中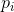，是分量信源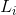的概率。

在物理上，所述情景就是：存在几个不同信源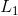，它们中的每一个都具有相同的统计结构（即，它们是各态历经的）。我们事先不知道将会使用哪个信源，但一旦在一个给定单纯分量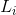中启动了一个序列，则它会根据该分量的统计结构无限持续下去。

作为一个例子，可以取得上面所定义过程中的两个，并假定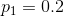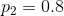，。可以通过以下方式获得由混合信源

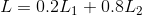
给出的序列：首先以概率0.2和0.8选择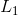或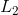，在此选择之后，由所选定的任意信源生成一个序列。

除非明确给出相反表述，否则我们将假定信源是各态历经的。利用这一假定，我们可以认为一个序列的均值等于可能序列系集(ensemble)的均值（出现偏差的概率为０）。例如，字符Ａ在一个具体无限长序列中的相对频率，以概率１等于它在序列系集中的相对频率。

如果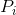是状态i的概率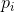，是由状态i向状态j变换的转换概率，则对于平稳过程，显然可以得出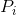，必须满足平衡条件：

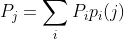
在各态历经情况下，可以证明，无论起始条件如何，当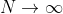时，在N个符号之后处于状态j的概率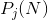趋近于平衡值。