6. 选择，不确定性和熵
我们已经将离散信源表示为马尔可夫过程。我们能不能定义一个量，用来在某种意义上，度量这样一个过程“生成”多少信息？甚至更进一步，度量它以什么样的速率生成信息？
假定有一个可能事件集，这些事件的发生概率为
。这些概率是已知的，但关于将会发生哪个事件，我们也就知道这么多了。我们能否找到一种度量，用来测量在选择事件时涉及多少种“选择”，或者输出中会有多少不确定性？
如果存在这样一种度量，比如说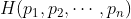
，那要求它具有以下性质是合理的：
H应当关于
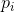连续。如果所有
都相等，即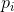
，则H应当是n的单调增函数。如果事件的可能性相等，那可能事件越多，选择或者说不确定性也更多。如果一项选择被分解为两个连续选择，则原来的H应当是各个H值的加权和。图6中展示了这一说法的含意。左侧的三个概率为
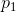。在右侧，我们首先以概率
在两种可靠性之间做出选择，如果发生第二种情况，则以概率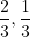
来进行另一次选择。最终结果将拥有和前面一样的概率值。在这一特例中，我们要求：
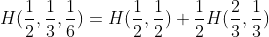
之所以存在系数
，是因为这一第二选择仅在一半时间内出现。
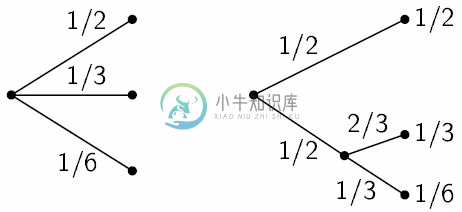
图6 分解一个具有三种可能性的选择
在附录2中，将确定以下结果：
定理2：唯一能够满足上述三条假定的H具有如下形式：
其中K是一个正常数。
在本文讨论的理论中，完全不需要这一定理，及其证明过程所做的一些假定。之所以给出这些内容，主要是为了提高后面一些定义的可信度。但是，这些定义的真正合理性体现在它们的推论中。
形如的量（常数K只不过是为了度量单位的选择）在信息论中扮演着核心角色，作为信息、选择和不确定性的度量。 将会看出，H的这一形式就是统计力学中某些公式中定义的熵，其中
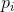是一个系统处于其相位空间中单元格i的概率。例如，这里的H可以是著名的波尔兹曼H定理中的H。我们会将称为概率集
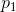的熵。如果x是一个随机变量，我将H(x)记为它的熵；因此x不是一个函数的参数，而是一个数值的记号，用于将它与H(y)区分开，H(y)是随机变量y的熵。
如果存在两种可能性，概率分别为p和q=1-p，则熵为：
H=-(p log p + q log q)
将它作为p的函数画在图7中。
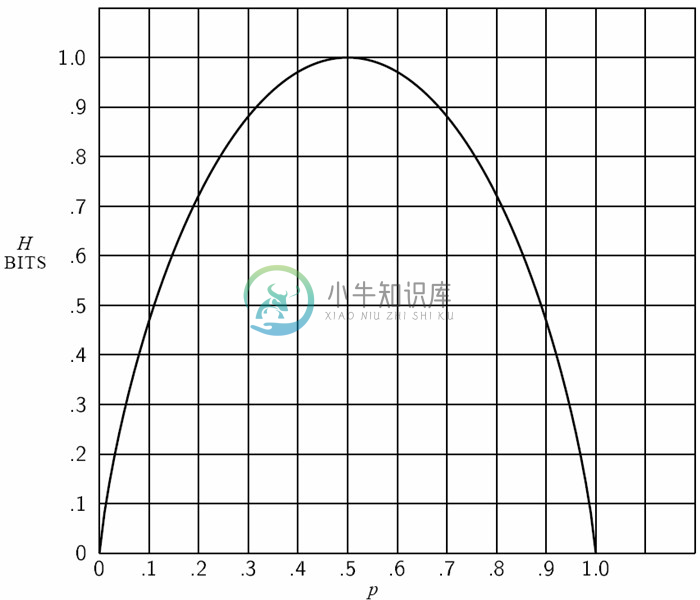
图7 当存在两种可能性，概率分别为p和(1-p)时的熵
量H有许多重要性质，这些性质进一步表明了它作为选择度量或信息度量的合理性。
当且仅当所有
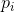中只有一个的取值为单位1，其他均为0时，H=0。仅当我们可以确定输出结果时，H消失。否则，H为正数。对于一个给定n，当所有
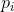都相等（即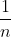
）时，H达到最大值log n。这种情景也正是我们在直觉上感受的最不确定情景。假定要考虑两个事件x和y，第一个事件有m种可能性，第二个事件有n种可能性。设p(i, j)是第一个事件为i、第二个事件为j的联合概率。这一联合事件的熵为：
而：
容易证明：
H(x, y)≤H(x) + H(y)
仅当这些事件独立时（即p(i, j)=p(i)p(j)），等号成立。一个联合事件的不确定性小于或等于各个不确定性之和。任何使概率
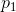趋于相等的改变都会使H增大。因此，如果
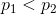，而且我们使
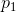增大，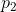
减小一个相等量，使
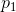和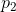
更接近相等，则H增大。更一般地来说，如果我们对
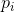执行以下形式的任意“均化”操作：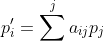
式中，，且所有
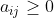，则H增大（有一种特殊情景除外，在这种情景中，这种变化就是
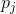的一个排列交换，H当然保持不变了）。和3中一样，假定有两个随机事件x和y，它们不一定相互独立。对于x可以取到的任意特定值i，存在一个y取j值的条件概率
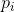。此概率给出如下：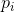
我们将y的条件熵
定义为关于每个x值，y的熵的加权平均，加权值为取得特定x值的概率。即：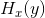
这个量用来度量当我们知道x时，y平均有多大的不确定性。代入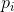
的值，得：
或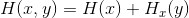
联合事件x, y的不确定性（或熵）是x的不确定性再加上当x已知时y的不确定性。由3和5可得：
因此
y的不确定性绝对不会因为知道了x值而增大。除非x和y是独立事件，否则y的不确定性会因为知道x值而下降，当两者独立时，该不确定性保持不变。