21. 函数系集的熵

考虑一个各态历经的带限函数系集，最高频率为W个周期/秒。设n个连续采样点的幅度的分布密度函数为：

。将该系集的熵（每自由度）定义为：

。

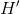我们还定义一个熵H（每秒），这次除以的不是n，而是n个采样的持续时间T（单位为秒）。由于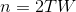，所以有。

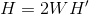当噪声为高斯白色热噪声时，有：

.

对于给定平均功率N，白噪声的熵最大。这一点是由上面给出的高斯分布的最大化属性得到的。

连续随机过程的熵有很多与离散情景类似的性质。在离散情况下，熵与长序列概率的对数相关联，与可能出现的长序列的数目相关联（这里所说的长，是在合理范围内）。在连续情况下，可以采用一种类似方式，将熵与一长串采样的概率密度的对数关联起来，与函数空间中的高概率体积相关联（这里所说的“高概率”，是指在合理范围内）。

更准确地说，如果假定对于所有值，在所有处都是连续的，则对于足够大的值，除了一个总概率小于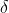的集合之外，对于任意选择的，都有

，

其中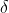和为任意小。如果将空间划分为大量小的单元格，则可以由各态历经性质推出以上结果。

H与体积的关系可以表述如下：同样假定有一个n维空间与对应。设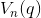是该空间中总概率为q的最小体积。如果q不等于0或1，则：

。

这些结果表明，对于大的n值，存在一个定义相当明确的高概率体积（至少在对数意义上是这样的），在这一体积内部，概率密度相对均匀一些（同样是指在对数意义上）。

在白噪声情况下，分布函数为：

。

由于该函数仅取决于，所以等概率密度的表面是一个球面，整个分布是球对称的。高密度区域是半径为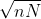。当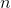时，位于半径为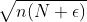的球体外部的概率趋近于0，该球体体积对数的倍趋近于。

在连续情况下，比较方便的做法不是处理系集的熵H，而是处理一个推导出来的量，我们称之为熵功率。其定义为：与原系集的带宽相等且具有相同熵的白噪声的功率。换言之，如果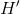为一个系集的熵，则熵功率为：

。

在几何图形中，这相当于用一个等体积球体的半径平方来衡量一个高密度体积。对于给定功率，白噪声的熵最大，所以任何噪声的熵功率都小于或等于其实际功率。