概率论08 随机变量的函数

优质

小牛编辑

127浏览

2023-12-01

随机变量的函数

在前面的文章中，我先将概率值分配给各个事件，得到事件的概率分布。

通过事件与随机变量的映射，让事件“数值化”，事件的概率值转移到随机变量上，获得随机变量的概率分布。

我们使用随机变量的函数，来定制新的随机变量。随机变量的函数是从旧有的随机变量到一个新随机变量的映射。通过函数的映射功能，原有随机变量对应新的随机变量。通过原有随机变量的概率分布，我们可以获知新随机变量的概率分布。事件，随机变量，随机变量函数的关系如下:

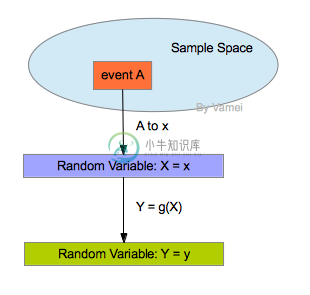
一个简单的例子是掷硬币。出现正面的话，我赢1个筹码，负面的话，我输1个筹码。那么，投掷一次，赢的筹码数是一个随机变量X，X可能取值为1和-1。因此X的分布为:

$$P(1) = 0.5$$

$$P(-1) = 0.5$$

换一个角度来思考，我们将正负面“换算”成输赢的钱。如果一个筹码需要10元钱买，那么投掷一次硬币，赢的钱是一个随机变量Y，且[$ Y = 10X $]。Y的分布为:

$$P(10) = 0.5$$

$$P(-10) = 0.5$$

Y实际上是随机变量X的一个函数。X的1对应Y的10，X的-1对应Y的-10。即[$Y = 10X $]

小总结，在上面的实验中，硬币为正面为一个事件。赢得的筹码数为一个随机变量X。赢得的钱是X的函数Y，它也是一个随机变量。

随机变量的函数还可以是多变量函数，[$Y = g(X_1, X_2, ..., X_n)$]。Y的值y对应的是多维空间的点[$(x_1, x_2,..., x_n)$]。比如掷硬币，第一次赢的筹码为[$X_1$]，第二次赢的筹码为[$X_2$]。我们可以构成一个新的随机变量[$Y = X_1 + X_2$]，即两次赢得的筹码的总和。

获得新概率分布的基本方法

一个核心问题是，如何通过X的概率分布，来获得[$Y=g(X)$]的概率分布。基本的思路是，如果我们想知道Y取某个值y的概率，可以找到对应的X值x的概率。这两个概率相等。

因此，我们使用如下方法来获得Y的概率。如果有函数关系[$Y=g(X_1, X_2, ..., X_n)$]，获得Y分布的基本方法是:

1. 通过[$Y=g(X_1, X_2, ..., X_n)$]，找到对应[$\{ Y \le y \}$]的[$(x_1, x_2, ..., x_n)$]区间I。

2. 在区间I上，积分[$ f(x_1, x_2, ..., x_n) $]，获得[$ P(Y \le y) $]

3. 通过微分，获得密度函数。

如果有函数关系[$ Y = X^2 $]，而X满足下面的分布:

$$f(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2}$$

对于任意[$y \ge 0$]来说，

$$F(y) = P(Y \le y) = P(X^2 \le y) = P(-\sqrt{y} \le X \le \sqrt{y}) $$

$$F(y) = \int_{-\sqrt{y}}^{\sqrt{y}}\frac{1}{\sqrt{2\pi}}e^{-x^2/2}dx = 2 \int_{0}^{\sqrt{y}}\frac{1}{\sqrt{2\pi}}e^{-x^2/2}dx$$

对上面的F(y)微分，即获得密度函数

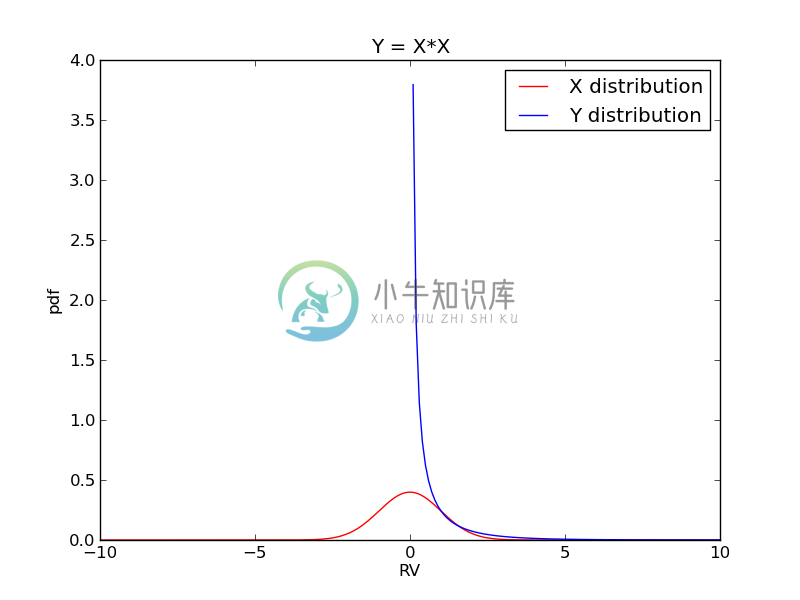
$$f(y) = \frac{1}{\sqrt{2\pi}}y^{-1/2}e^{-y/2}, 0 \le y \le \infty$$

绘制密度函数

import numpy as np
import matplotlib.pyplot as plt

pi = np.pi

x = np.linspace(-10, 10, 200)
y = np.linspace(0.1, 10, 100)

fx = 1/np.sqrt(2*pi)*np.exp(-x**2/2)
fy = 1/np.sqrt(2*pi)*(y**(-1/2))*np.exp(-y/2)

plt.plot(x, fx, color = "red", label="X distribution")
plt.plot(y, fy, label="Y distribution")

plt.title("Y = X*X")
plt.xlabel("RV")
plt.ylabel("pdf")

plt.legend()

plt.show()

上面的例子展示的是单变量函数，我们看一个多变量函数的例子。即[$ Y=g(X_1, X_2, ..., X_n) $]，且已知[$X_1, X_2, ..., X_n$]的联合分布为[$f(x_1, x_2, ..., x_n)$]。我们需要找到满足[$ g(x_1, x_2, ..., x_n) \le y $]的区间。

比如，[$ Y = X_1 + X_2 $]，且[$X_1, X_2$]满足如下分布:

$$f(x_1, x_2) = \frac{1}{2 \pi} \exp \left( -\frac{1}{2} \left( x_1^2 + x_2^2 \right) \right)$$

为了让[$x_1 + x_2 \le y$]，我们可以让[$x_1$]任意取值，而让[$x_2 \le y - x_1$]

$$F_Y(y) = \int_{-\infty}^{\infty} \int_{-\infty}^{y - x_1} f(x_1, x_2) dx_2dx_1 $$

让x_2 = v - x_1，有

$$F_Y(y) = \int_{-\infty}^{\infty} \int_{-\infty}^{y} f(x_1, v - x_1)dvdx_1 = \int_{-\infty}^{y} \int_{-\infty}^{\infty}f(x_1, v - x_1)dvdx_1$$

微分，可得y的分布为:

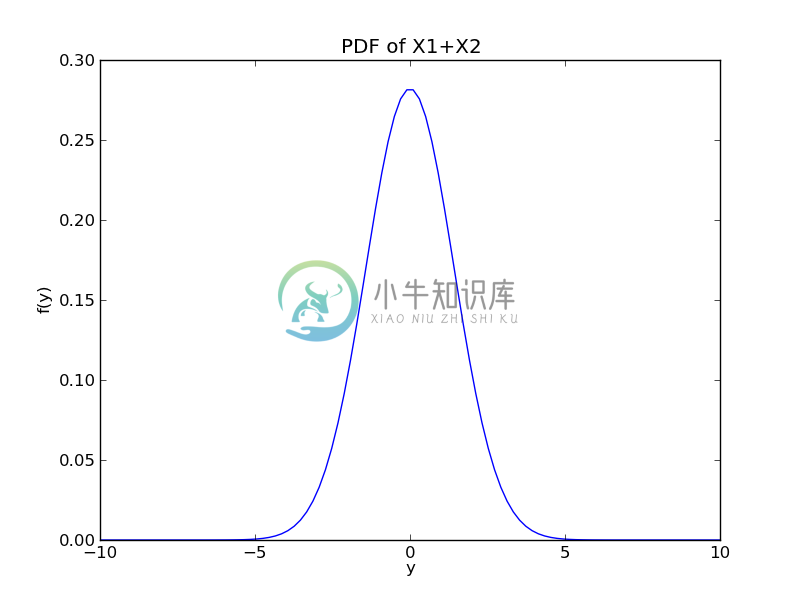
$$ f_Y(y) = \int_{-\infty}^{\infty} f(x_1, y - x_1) dx_1 = \int_{-\infty}^{\infty} \frac{1}{2 \pi} \exp \left( -\frac{1}{2} \left( x_1^2 + (y - x_1)^2 \right) \right) dx_1 $$

上述方程也可以使用数值方法求解:

代码如下:

# By Vamei

import numpy as np
import scipy.integrate
import matplotlib.pyplot as plt
pi = np.pi

'''
core of the integral
'''
def int_core(y):
    f = lambda x: 1.0/(2*pi)*np.exp(-0.5*(x**2 + (y-x)**2))
    return f

'''
calculate f(y)
'''
def density(y):
    rlt = scipy.integrate.quad(int_core(y), -np.inf, np.inf)
    return rlt[0]

# get distribution
y  = np.linspace(-10, 10, 100)
fy = map(density, y)

plt.plot(y, fy)
plt.title("PDF of X1+X2")
plt.ylabel("f(y)")
plt.xlabel("y")
plt.show()

上面的int_core()函数是一个闭包，它表示积分核部分。density()函数用于求某个y值下的积分结果。

(我们也可以利用解析的方法，推导出f(y)满足分布[$N(0, \sqrt{2})$]。如果有微积分基础，可以将此作为练习。)

单变量函数的通用公式

上面求新的随机变量分布的步骤较为繁琐。在一些特殊情况下，我们可以直接代入通用公式，来获得新的分布。

(通用公式实际上是从基本方法推导出的数学表达式)

对于单变量函数来说，如果[$Y=g(X)$]，g是一个可微并且单调变化的函数 (在该条件，存在反函数[$g^{-1}$]，使得[$X=g^{-1}(Y))$]。那么我们可以使用下面的通用公式，来获得Y的分布:

$$f_Y(y) = f_X(g^{-1}(y)) \cdot \frac{d}{dy}g^{-1}(y)$$

假设X为标准分布，即[$N(0, 1)$]，且[$Y = 5X + 1$]，那么[$g^{-1}(y) = (y - 1)/5$]，因此:

$$f_Y(y) = f_X((y-1)/5) \cdot (1/5) = \frac{1}{5\sqrt{2\pi}}e^{-(y-1)^2/(2 \times 25)}$$

可以看到，新的分布是一个[$\mu = 1, \sigma=5$]的正态分布，即[$N(1, 5)$]

并不是所有的函数都有反变换，所以这里的“通用”公式并不能适用于所有的情况。

多变量函数的通用公式

在一些特殊情况下，我们可以使用多变量函数的通用公式。

如果[$U=g_1(X, Y), V=g_2(X, Y)$]，且存在反变换，使得

$$X = h_1(U, V)$$

$$Y = h_2(U, V)$$

那么，我们可以通过如下公式，从X,Y的分布获得U,V的联合分布:

$$f_{UV}(u, v) = f_{XY}(h_1(u, v), h_2(u, v))|J|$$

J表示雅可比变换(Jacobian tranformation)，表示如下

$$J = \left| \begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array} \right| =\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u} $$

如果X和Y是独立的随机变量，且有相同的分布$$f(x) = e^{-x}, x \ge 0$$。如果[$U = X+Y, V= Y$]，求U和V的联合分布。

由于X和Y独立，所以

$$f_XY(x, y) = f(x)f(y) = e^{-x}e^{-y}$$

根据[$ U=X+Y $]，[$V= Y$]，可以得到[$ u \ge 0, v \ge 0$], 且有:

$$X = U - V$$
$$Y = V$$

因此

$$f(u, v) = e^{-(u-v)}e^{-v} = e^{-u}, u \ge 0, v \ge 0$$

总结

通过随机变量的函数，我们可以利用已知随机变量，创建新的随机变量，并获得其分布。