概率论02 概率公理
概率论早期用于研究赌博中的概率事件。赌徒对于结果的判断基于直觉,但高明的赌徒尝试从理性的角度来理解。然而,赌博中的一些结果似乎有矛盾。比如掷一个骰子,每个数字出现的概率相等,都是1/6。然而,如果有两个骰子,那么出现的2到12这些数字的概率却不相同。概率论这门学科正是为了搞清楚这些矛盾背后的原理。
早期的概率论是一门混合了经验的数学学科,并没有严格的用语。因此,概率论在数学的精密架构下,显得有些异类。许多名词,如“概率”等,一定程度上是按照人们的直觉来定义的。1933年,俄国数学家Andrei N. Kolmogorov建立了概率论的公理化体系,严格定义了概率论的语言。正如现代数学的其他学科一样,概率论的公理化体系同样基于集合论。公理化的概率论体系基于几条简单易懂的公理,衍生出整个概率论的体系。学习这个公理化的体系,可以消除直觉中的许多混淆。这一公理体系的核心是“概率测度”。
实验与样本空间
任何一个过程,如果它的结果是随机的(无法事前知道),那么该过程就称为一个实验。实验所有可能的结果组成一个集合(set),叫做样本空间(sample space),用[$\Omega$]表示。我们看下面实验的样本空间:
实验1. 连续掷一个硬币两次:
$$\Omega = \{ HH, HT, TH, TT \}$$
H表示正面,T表示反面。上面括号里包含了所有可能的结果:正正,正反,反正,反反。

实验2. 打印机的队列最多允许10个工作。某时刻的工作数目:
$$\Omega = \{ 0, 1, 3, ..., 9, 10 \}$$

实验3. 开车经过两个路口,遇到的红绿灯情况:
$$\Omega = \{ rr, rg, ry, gg, gr, gy, yy, yr, yg \}$$
r表示红灯,g表示绿灯,y表示黄灯。
(利用计数原理,我们可以知道所有可能结果的总数为9)

对于概率论来说,集合是“如来佛的手掌心”。事实上,整个现代数学体系都是建立在集合论的基础上。集合本身没有什么神秘的,就是一些元素的集合。数学的关键是不同集合的特性、集合内部的结构和集合之间的关系。看似平常的集合给数学带来许多意想不到的结果。
事件
样本空间包含了概率论研究的基本元素,也就是实验的结果。它们好象化学里的原子。在掷撒子的游戏中,1,2,3,4,5,6,这些结果就构成了我们的原子。然而,就像赌徒只对“大”和“小”感兴趣一样,在许多时候,我们会对分子那样的原子集合更感兴趣。在概率论里,这样的“分子”就是样本空间的子集。样本空间的一个子集,被称为一个事件(event)。比如说,在实验1中,第一次投掷为正面的所有结果构成子集,即一个事件。该事件包含有两个元素:
$$A = \{ (H,H), (H,T) \}$$
再比如,第二次投掷为正面也构成一个事件,即
$$B = \{ (H,H), (T,H) \}$$
我们可以将事件理解为一些特定结果的合集。通过事件,我们可以将结果“聚合”,从而在高一层的单位上进行概率研究。
既然事件是样本空间的一个子集,那么事件可以有补集。事件A的补集包含所有不属于A的样本空间元素。
$$A^c = \{ TH, TT \}$$
该补集代表的事件为: 第一次投掷是反面。
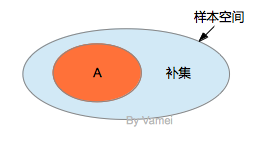
补集
两个集合可以有交集和并集运算。我们以集合A和集合B为例。
$$C = A \cap B$$
交集C中包含了所有既在A中又在B中的元素。事件C表示第一次为正面且第二次为正面。[$C = \{ (H,H) \}$]
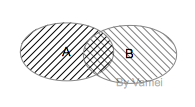
交集: 交叉阴影区域
$$D = A \cup B$$
并集D中包含了所有在A中或者在B中的元素。事件D表示第一次为正面或者第二次为正面,[$D = \{ (H,H), (T,H), (H,T) \}$]
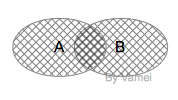
并集: 交叉阴影区域
空集[$\Phi$]是一个不包含任何元素的集合。如果两个集合的交集为空集,即[$M \cap N = \Phi $],那么这两个集合不相交。在概率论中,不相交的两个事件互斥。
和加法一样,集合的交并集运算同样有运算法则。这些法则可以如上面那样,画出集合图形,来辅助理解。
交换律
$$A \cup B = B \cup A$$
$$A \cap B = B \cap A$$
结合律
$$ (A \cup B) \cup C = A \cup (B \cup C)$$
$$ (A \cap B) \cap C = A \cap (B \cap C)$$
分配律
$$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$$
$$(A \cap B) \cup C = (A \cup C) \cap (B \cup C)$$
概率测度
我们上面定义了一些基本用语,即“实验”,“样本空间”,“事件”。我们下面要给“分子”上色:引入概率的概念。我们用函数来给每个事件分配一个概率,即分子和颜色的对应关系。
概率测度是基于样本空间[$\Omega$]的一个函数P。这个函数P定义了从样本空间的子集(即事件)到实数的映射,且满足下面的条件:
1. [$P(\Omega) = 1$]
2. 如果[$A \subset \Omega$], 那么[$P(A) \ge 0$]
3. 如果[$A_1$]和[$A_2$]不相交,那么
$$P(A_1 \cup A_2) = P(A_1) + P(A_2)$$
“概率测度”是一个有些抽象的概念。“测度”这个词是在提示我们概率定义的基础是“测度论”。粗糙的说,“测度论”用于研究一个集合的“大小”或者说“面积”。更严格的说,就像概率一样,“测度”是集合的子集到实数的一个映射。比如一个正方形的面积为6,实际上是说,一个点的集合(正方形)的某个“测度”为6,即点的集合和实数6对应。“面积”的一个关键特点是可加。比如我们买地的时候,如果两块地不重叠,那么它们的面积总和是两个各自面积的和。概率测度有相同的特点,就是上面的第3点。第1,2两点是概率的基本特征,即所有情况的概率总和为1,而概率值不为负。基于这样一种直观但不严格的类比,我们可以把概率(也就是“概率测度”)想象成“集合的面积”。而“样本空间的总面积为1”。
以上是概率论的公理体系。利用上面的定义以及集合论工具,我们会进一步建立起概率论的体系。但要注意的是,上面公理化的定义,尽管严谨,但并没有说明“概率是什么”,而只是说“概率那个人啊,它应该长的方脸,长鼻子,小眼镜”。这有些像编程中的"duck typing",也就是根据对象的动作或者特点,来定义对象。即使是今天,概率的本质也存在争议。主流的观点分为两派,即频率观点和贝叶斯观点。在频率观点中,如果我们以相同的条件重复尝试N次,那么如果某个事件出现了n次,那么该事件的概率为[$P(A) = n/N$]。在贝叶斯观点中,概率代表了主观上对某一论断的信心。尽管对概率的理解不同,这两个流派都开衍生出了非常有用的工具。
另一方面,定义也没有告诉我们如何确定函数P,即如何计算概率测度。很多时候,函数P的确定依然基于一些假设和一定程度的直觉。比如在等概率条件下,我们利用计数方法,来获得概率。比如一枚硬币出现正反两面的概率相同,结果总数为2,那么[$P(H) = 1/2$]。这也正是我们第一讲中讲解计数的目的所在。然而在其他情况下,比如不均匀硬币,我们不能简单的用1除以结果总数。我们可以利用频率观点,大量重复实验,来获得P函数。
Python中的集合
集合这一数据结构在多种语言中都有。比如Python中的集合:
A = set([1, 2, 3, 4]) B = set([3, 4, 5, 6]) print(A & B) # intersection print(A | B) # union print(A - B) # difference, element in A, and not in B print(A ^ B) # symmetric difference, (A | B) - (A & B)
上面实现了集合的运算。
再比如,我们可以用in来判断元素是否属于集合,以及用>, >=, <, <=来判断两个集合的归属关系,比如一个集合是另一个集合的子集。
A = set([1, 2]) B = set([1, 2, 3]) print(1 in A) # element print(A < B) # subset
set是一个数据容器,len(), max(), min()函数同样可用于set,分别返回集合中元素总数,集合最大值,集合最小值。此外,set还有一些方法,比如下面的增加和删除元素,注意set中不会有重复的元素:
A = set([1, 2]) A.add(5) # add an element print(A) A.remove(2) # remove an element print(A) A.add(1) print(A) # a set has no repeated elements
上面的set中元素都为整数,还可以是其他的任意对象。
练习: 利用Python,验证集合的运算律。
总结
样本空间,事件
互斥事件
概率测度
欢迎继续阅读“数据科学”系列文章

