概率和似然的区别?
参考回答：
概率是指在给定参数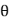
的情况下,样本的随机向量X=x的可能性。而似然表示的是在给定样本X=x的情况下,参数
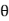为真实值的可能性。一般情况,对随机变量的取值用概率表示。而在非贝叶斯统计的情况下,参数为一个实数而不是随机变量,一般用似然来表示。
-
本文向大家介绍最大似然估计和最大后验概率的区别?相关面试题，主要包含被问及最大似然估计和最大后验概率的区别?时的应答技巧和注意事项，需要的朋友参考一下 参考回答： 最大似然估计提供了一种给定观察数据来评估模型参数的方法,而最大似然估计中的采样满足所有采样都是独立同分布的假设。最大后验概率是根据经验数据获难以观察量的点估计,与最大似然估计最大的不同是最大后验概率融入了要估计量的先验分布在其中,所以最
-
我的数据集是 我想计算prob(Q2=1，给定q4=1)，根据我的知识，它应该是1。但是当我在R中使用following命令时 返回0.5 第二个问题是如果我将数据集更改为 当我使用上面的数据并计算上面的概率时，它返回1。当我不改变Q2和Q4时，概率怎么会改变。 我的想法是，在这两种情况下，概率应该是相同的1。 为什么它只是随着其他参数Q1和q3的变化而变化。我认为它应该改变，因为P(q2=1/q
-
在概率公理中，我们建立了“概率测度”的概念，并使用“面积”来类比。这是对概率的第一步探索。为了让概率这个工具更加有用，数学家进一步构筑了“条件概率”，来深入探索概率中包含的数学结构。我们可以考虑生活中常见的一个估计： 三个公司开发一块地。A占地20%，B占地30%，C占地50%。三个公司规划的绿地占比不同：A土地中40%规划为绿地，B土地中的30%规划为绿地，C土地中的10%规划为绿地。我想选择绿
-
概率论早期用于研究赌博中的概率事件。赌徒对于结果的判断基于直觉，但高明的赌徒尝试从理性的角度来理解。然而，赌博中的一些结果似乎有矛盾。比如掷一个骰子，每个数字出现的概率相等，都是1/6。然而，如果有两个骰子，那么出现的2到12这些数字的概率却不相同。概率论这门学科正是为了搞清楚这些矛盾背后的原理。 早期的概率论是一门混合了经验的数学学科，并没有严格的用语。因此，概率论在数学的精密架构下，显得有些异
-
面试时如果被问了一个概率题，那就要小心了，面试官可能要刷人了！ 面试概率题的特点： 题面不复杂 短时间可以解答 会者不难 RoadMap 概率论基础 TODO 常见面试题 古典概型 在一个有限的集合 S 中随机抽取一个元素，求该元素属于子集 T 的概率； 概率 p = 子集 T 中元素的数量 / 集合 S 中元素的数量 示例： 一枚均匀的骰子掷到 1 的概率： S = {1,2,3
-
问题内容： 我很好奇，我该如何在Java中实现概率？例如，如果变量显示的机会是1/25，那么我将如何实现呢？还是其他可能性？请指出我的大致方向。 问题答案： 您将使用Random生成一个随机数，然后根据文字对其进行测试以匹配您尝试实现的概率。 因此给出： 将有1/25的可能性为真（因为返回从0到25（但不包括25）的任何数字的可能性均是偶数）。 您当然也必须这样做。 如下面所指出的，如果获得多个随