概率论13 中心极限定律

在整个概率论中，核心的问题是随机变量的分布。正如我们在离散分布和连续分布中看到的，分布有许多种类。更夸张的是，在满足概率公理的前提下，我们完全可以自行设计分布。想像一下，如果有一天数学书上印一个Vamei分布，这是多么美好的事情啊！然而，这一愿望并不那么容易实现。那些“名流”分布，比如“泊松”，“高斯”，“伯努利”分布，往往在理论上很重要，所以得到了数学家的深入研究。“知名”分布的特性(比如它们的期望、方差、累计概率函数)可以很容易在数学手册中找到，这些研究成果也成为概率论“军火库”的重要部分。

另一方面，概率分布是否存在什么共性呢？我们的许多结论都是依赖于分布的具体类型。对于一个分布成立的结论，对于另一种分布可能并不成立。一个对任意分布都成立的结论可以大大简化我们的研究。这在自然科学和社会科学的研究中异常重要。在这些学科的研究中有许多随机变量。比如说，为了研究金矿，往往需要知道石头中含金量X的概率分布。然而，这些随机变量的分布类型不可能提前获知 (甚至于永远不能准确的知道)。这样的话，整个研究就被停在了第一步。如果我们可以得出一个对任意分布都成立的结论，那么我们就可以沿着这个结论继续进行下去。

自然有时候比我们想像的慷慨，它给出了一个概率论中相当核心的一组定律：中心极限定律(central limit theorem)。这组定律不但对于任意分布都成立，还特别提示我们：要特别注意正态分布。我们下面看看，中心极限定律是如何说的。

中心极限定律

先来看中心极限定律的一个版本:

随机变量[$X_1, X_2,..., X_n$]是相互独立的随机变量，并有相同的分布(IID, independent and identically distributed)。分布的期望为[$\mu$]，方差为[$\sigma^2$]，[$\mu,\sigma$]都为有限值，且[$\sigma \ne 0$]。这些随机变量的均值为[$\bar{X} = \frac{1}{n} \sum_{i=1}^{n}X_i$]。让[$\zeta_n = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}}$]，那么

$$\lim_{n \rightarrow \infty} P(\zeta_n \le z) = \Phi(z)$$

其中[$\Phi(z)$]是标准正态分布的分布函数。

简单来说，我们寻找n个IID随机变量的均值[$\bar{X}$]。当n趋进无穷时，这个均值(一个新的随机变量)趋近一个正态分布。

(通过[$\zeta_n$]的变换，可以从正态分布的[$\bar{X}$]导出标准正态分布[$\zeta_n$]。)

演示中心极限定律

我们下面取n个IID随机变量，让它们都符合[$\lambda = 1$]的指数分布，并观察它们均值的分布状况。为了观察它们的分布，我们使用随机数生成器，来进行10000次采样。即进行100000次实验，每次实验获得一组随机变量的取值，得到一个均值。总共获得10000个均值。绘制均值分布的直方图。

分三种情况，分别让n等于1，20， 100:

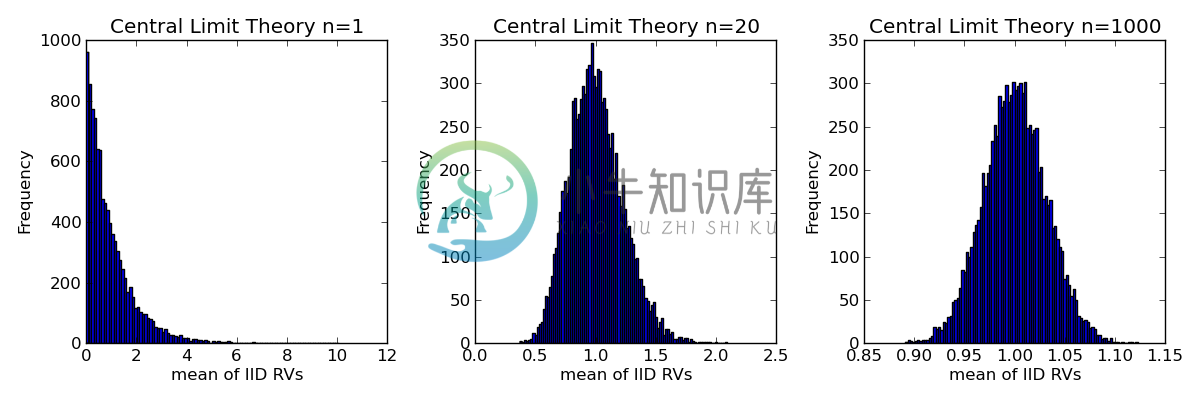
在第一种情况下,[$\bar{X} = X_1/1 = X_1$]，即[$\bar{X}$]本身是指数分布。

在第二、三种情况下，均值的分布越来越偏离一个指数分布，分布的形状不断趋近于一个正态分布。

代码如下：

# By Vamei 
# Central Limit Theory 
# X is exponential distribution with lambda = 1 

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import expon

# Get one sample of (X1 + X2 + ... + XN)/N 
def sample_mean(N):
    # exponential distribution, with lambda = 1 
    one_sample = expon.rvs(scale = 1, size = N)
    return one_sample.mean()

# Increase N: 1, 20 , 1000. 
# Demo of Central Limit Theory in histogram
plt.figure(figsize=(12, 4))
for N, subp in zip([1, 20, 1000], [131, 132, 133]):
    # generate samples 
    all_means = np.array([sample_mean(N) for i in range(10000)])

    # plot figure
    plt.subplot(subp)
    plt.hist(all_means,bins=100,color="blue")
    plt.title('Central Limit Theory n=%i' % N)
    plt.xlabel('sample means')
    plt.ylabel('Frequency')

plt.tight_layout()
plt.savefig('./central_limit.png', dpi=None, facecolor='w')

练习：这段代码检验的是指数分布的均值。可以改写成检验其它分布是否符合中心极限定律，比如均匀分布的均值。

证明

我将使用矩生成函数来证明上面的定律。假设[$X_i - \mu$]的矩生成函数为[$M(t)$]。因此，[$M'(t) = \mu, M^{(2)}(t) = \sigma^2$]。

当n趋近无穷时，[$t/(\sigma \sqrt{n})$]趋近0。M(t)可以展开为:

$$M(t) = 1 + \frac{1}{2}\sigma^2t^2 + o(t^2)$$

[$o(t^2)$]表示比[$t^2$]更高阶的t的乘方。

根据矩生成函数的性质，[$\zeta_n$]的矩生成函数写为

$$M_{\zeta_n} = \left[M \left(\frac{t}{\sigma \sqrt{n}} \right) \right]^n = \left( 1 + \frac{t^2}{2n} + o(t^2/n)\right)^n $$

[$o(t^2/n)$]表示，当n趋于无穷时，早于[$t^2/n$]消失的项。

(根据微积分，证明从略)：当n趋近于无穷时，上面的表达式趋近：

$$M_{\zeta_n}(t) \rightarrow e^{t^2/2}$$

这正是标准正态分布的矩生成函数。因此[$Z_n$]的分布趋近于标准正态分布。

上面介绍的中心极限定律有一个先决条件，即产生均值的N个随机变量为IID(独立、同分布)随机变量。在其它的版本的中心极限定律中，各个随机变量可以不完全独立。事实上，中心极限定律是一个还在积极研究中的领域。

花边

中心极限定律的原型可以追溯到18世纪de Moivre的研究。他经过实验发现，大量正面抛硬币的话，结果(1：正面，0：反面)的均值是一个正态分布。这里，de Moivre研究的分布是多个伯努利分布的随机变量的均值。

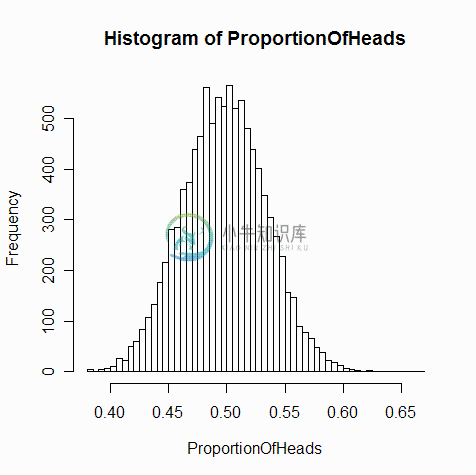
硬币投掷：均值的分布

(想像一下，当时没有计算机，更别说随机数生成器了。为了检验结果，de Moivre真的投了几千次硬币…… 数学家是很神奇的动物)

为了更加直观的理解中心极限定律的结果。我们来设想一下，如果一个大米缸中混装了黑白两种米，各占一半。从中随便抓一把，这一把中有n个米粒。如果n比较小的话，那么很有可能出现一些极端值，比如n = 3，出现三个纯白的米粒。但是，如果“一把”很大，比如1000颗米粒，那么出现1000个米都是白色的概率很小，而白米和黑米一半一半的概率很大，也就是一个类似于正态分布的分布方式。

我们可以将中心极限定律方便的用于许多统计问题。需要注意的是，中心极限定律要求n趋近无穷。在实际应用中，我们往往让n等于一个“足够”大的数，比如上面的1000。这个数字是否足够大呢？这取决于X是什么样的分布。对于某些分布来说，均值分布趋近于正态分布的速度很慢，这要求我们采用更大的n值。

总结

中心极限定律（均值趋近正态分布）