概率论05 离散分布
我们已经知道什么是离散随机变量。离散随机变量只能取有限的数个离散值,比如投掷一个撒子出现的点数为随机变量,可以取1,2,3,4,5,6。每个值对应有发生的概率,构成该离散随机变量的概率分布。
离散随机变量有很多种,但有一些经典的分布经常重复出现。对这些经典分布的研究,也占据了概率论相当的一部分篇幅。我们将了解一些离散随机变量的经典分布,了解它们的含义和特征。
伯努利分布
伯努利分布(Bernoulli distribution)是很简单的离散分布。在伯努利分布下,随机变量只有两个可能的取值: 1和0。随机变量取值1的概率为p。相应的,随机变量取值0的概率为1-p。因此,伯努利分布可以表示成:
$$P(X=k) = \left\{ \begin{array}{rcl} p & for & k=1 \\ 1-p & for & k=0 \end{array} \right.$$
投掷一次硬币,出现正面,记录为1,出现背面,记录为0。这样我们就有一个伯努利随机变量。如果硬币是均匀的,那么[$p=0.5$]。如果硬币是不均匀的,比如硬币出现正面的概率为0.8,那么[$p=0.8$]。我们可以绘制此分布如下:
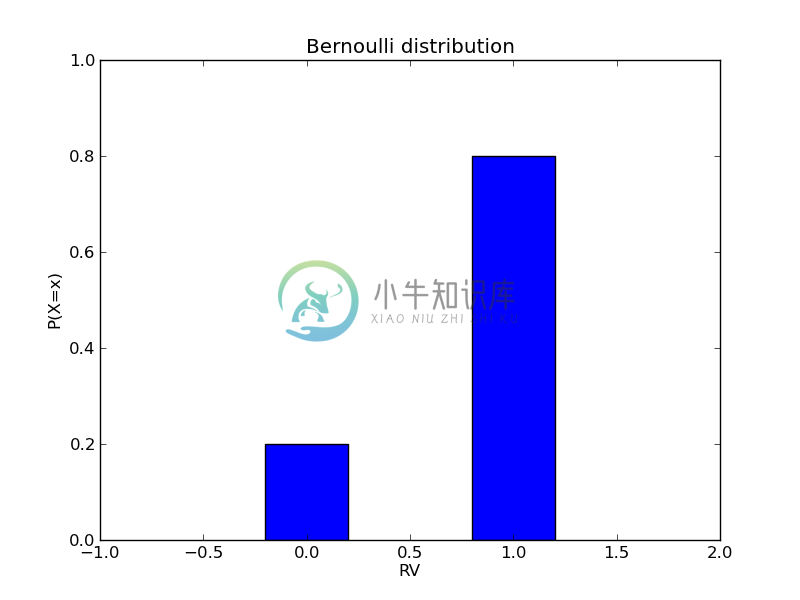
代码如下:
# By Vamei
plt.bar([-0.2,0.8],[0.2, 0.8],width=0.4) # bar plot
plt.xlim([-1, 2]) # axis range
plt.ylim([0.0, 1.0])
plt.title("Bernoulli distribution") # figure title
plt.xlabel("RV")
plt.ylabel("P(X=x)")
plt.show()在scipy.stats中,有直接表达伯努利分布的函数bernoulli。事实上,在scipy.stats中,有许多常见的分布函数。
# By Vamei from scipy.stats import bernoulli rv = bernoulli(0.8) x = [-1, 0, 1, 2] print(rv.cdf(x))
上面,我们创建了一个[$p=0.8$]的伯努利随机变量,并计算该随机变量在不同点的累积分布函数(CDF)。
二项分布
为了理解二项分布是如何出现的,我们假设下面情况:进行n次独立测试,每次测试成功的概率为p(相应的,失败的概率为1-p)。这n次测试中的“成功次数”是一个随机变量。这个随机变量符合二项分布(binomial distribution)。
二项分布可以从计数的角度来理解。n次测试,如果随机变量为k,意味着其中的k次成功,n-k次失败。从n次实验中挑选k个,根据计数原理,共有[$\left( \begin{array}{c} n \\ k \end{array} \right)$]种可能。其中的每种可能出现的概率为[$p^k(1-p)^{n-k})$]。因此,二项分布可以表示成为:
$$P(X=k) = \left( \begin{array}{c} n \\ k \end{array} \right) p^k (1-p)^{n-k}$$
$$k = 0,1,2,...,n$$
(“二项分布”的命名原因是,上面的P(X=k)等于二项式[$(p + (1-p))^n$])二项式展开的第k项。)
我们进行连续的10次打靶,如果每次中靶的概率为0.7, 那么在10次打靶中,打中靶的次数就是一个符合二项分布的随机变量。在这样的假设下,[$n=10$],[$p=0.7$],k可以取值从0到10之间的任意整数。利用scipy.stats中的binom函数,我们可以绘制此分布如下:
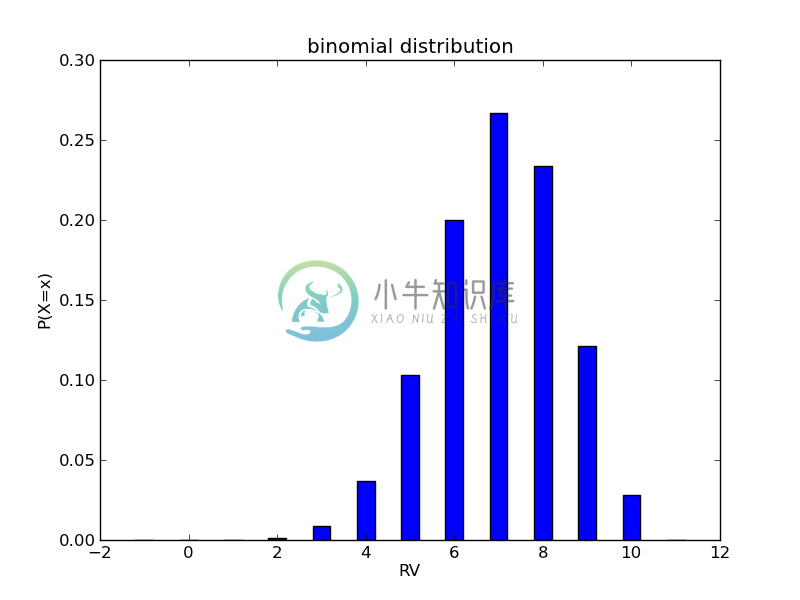
[$x=0$]和[$x=1$]概率不为0,只是值太小,没有在图中显现出来。
代码如下:
# By Vamei
from scipy.stats import binom
rv = binom(10, 0.7)
x = np.arange(-1, 12, 1)
y = rv.pmf(x)
plt.bar(x-0.2, y, width=0.4)
plt.title("binomial distribution")
plt.xlabel("RV")
plt.ylabel("P(X=x)")
plt.show()泊松分布

泊松
泊松分布(Poisson distribution)是二项分布的一种极限情况,当[$p \rightarrow 0$],[$n \rightarrow +\infty$],而[$np = \lambda$]时,二项分布趋近于泊松分布。这意味着我们进行无限多次测试,每次成功概率无穷小,但n和p的乘积是一个有限的数值。
泊松分布用于模拟低概率事件,比如地震。地震是很低概率的事件,我们想知道一段时间,比如十年内某地发生地震的总数,可以将十年划分为n个小时间段,每个时间段内地震发生的概率为p。我们假设小时间段很短,以致于不可能有两次地震发生在同一小时间段内,那么地震的总数是一个随机变量,趋近于泊松分布。
泊松分布的关键特征是,随机变量的取值与区间的长短成正比。这里的区间是广义的,它既可以表示时间,也可以表示空间。泊松分布有一个参数[$\lambda$],我们可以将泊松分布写成如下形式:
$$P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda}$$
$$k=0,1,2,...$$
[$\lambda = 1$]和[$\lambda = 5$]的泊松分布如下:
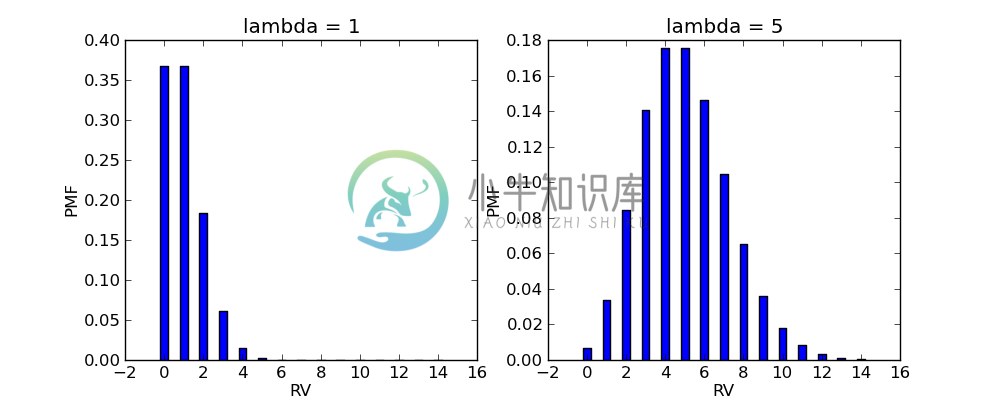
可以看到,[$\lambda$]决定了泊松分布的“重心”所在。比如地震的例子中,[$\lambda$]越大,k取大值的可能性越大,越有可能发生更多次的地震。我们将在统计中看到,如何利用观测的数据,来估计[$\lambda$]的取值。
代码如下:
# By Vamei
# use poisson function
from scipy.stats import poisson
rv1 = poisson(1)
x = np.arange(0,15)
y1 = rv.pmf(x)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.bar(x-0.2, y1, width=0.4)
plt.title("lambda = 1")
plt.xlabel("RV")
plt.ylabel("PMF")
plt.subplot(122)
rv2 = poisson(5)
y2 = rv2.pmf(x)
plt.bar(x-0.2, y2, width=0.4)
plt.title("lambda = 5")
plt.xlabel("RV")
plt.ylabel("PMF")
plt.show()几何分布
假设我们连续进行独立测试,直到测试成功。每次测试成功的概率为p。那么,到我们成功时,所进行的测试总数是一个随机变量,可以取值1到正无穷。这样一个随机变量符合几何分布(geometric distribution)。
随机变量取值为k时,意味前面的k-1次都失败了。因此,我们可以将几何分布表示成:
$$P(X=k)=(1-p)^{k-1}p$$
$$k=1,2,...$$
假设我们进行产品检验。产品的合格率为0.65。我们需要检验k次才发现第一个合格产品,k的分布表示如下:
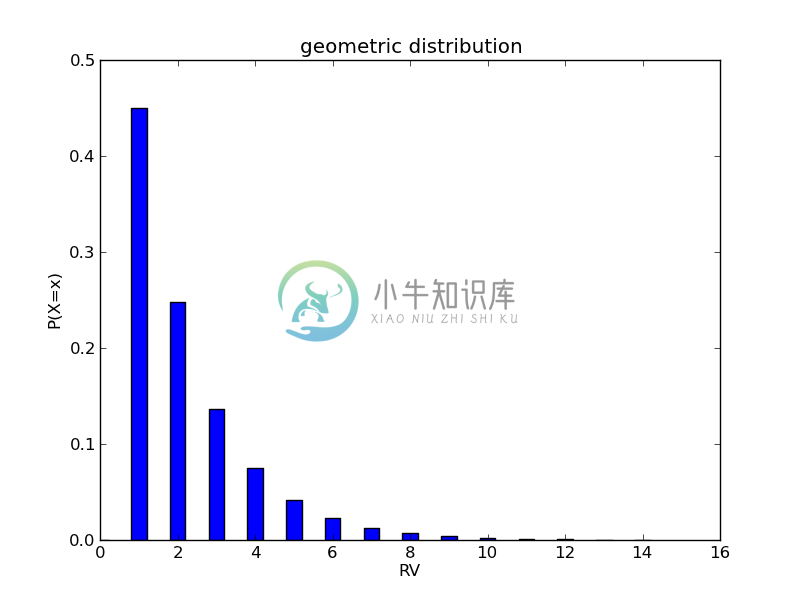
可以看到,几何分布的概率质量函数呈递减趋势。我们也可以从表达式中得到该特征。
代码如下:
# By Vamei
from scipy.stats import geom
rv = geom(0.45)
x = np.arange(-1, 15, 1)
y = rv.pmf(x)
plt.bar(x-0.2, y, width=0.4)
plt.ylim([0, 0.5])
plt.title("geometric distribution")
plt.xlabel("RV")
plt.ylabel("P(X=x)")
plt.show()负二项分布
几何分布实际上是负二项分布(negative geometric distribution)的一种特殊情况。几何分布是进行独立测试,直到出现成功,测试的总数。负二项分布同样是进行独立测试,但直到出现r次成功,测试的总数k。r=1时,负二项分布实际上就是几何分布。
在连续的r次测试时,我们只需要保证最后一次测试是成功的,而之前的k-1次中,有r-1次成功。这r-1次成功的测试,可以任意存在于k-1次测试。因此,负二项分布的表达式为:
$$P(X=k) = \left( \begin{array}{c} k-1 \\ r-1 \end{array} \right) p^r (1-p)^{k-r}$$
$$k = 1,2,...$$
练习: (可以使用scipy.stats中的ngeom函数来表示负二项分布) 假设我们进行产品检验。产品的合格率为0.65。我们需要检验k次才共发现3个合格产品。绘制随机变量k的概率分布。
超几何分布
一个袋子中有n个球,其中r个是黑球,n-r是白球,从袋中取出m个球,让X表示取出球中的黑球的个数,那么X是一个符合超几何分布(hypergeometric distribution)的随机变量。
练习: 推导超几何分布的概率质量函数,并绘制其概率分布。
总结
离散随机变量比较直观,容易理解。我们在这里介绍了一些经典分布,即随机变量取值的概率。

