从数据集得到的自定义概率分布的R-随机绘图

Question

我有一个R数据帧my_measures（它是一个大得多的10k+行数据帧的子示例），如下所示：

> glimpse(my_measurements)
Observations: 300
Variables: 2
$ measurement_id <int> 2, 27, 36, 39, 41, 44, 118, 121, 125, 127, 132, 134, 148...
$ value          <dbl> 0.9746835, 1.0000000, 1.0000000, 1.0000000, 1.0000000, 0...

以下是dput(my_meansactions)输出：

structure(list(measurement_id = c(2L, 27L, 36L, 39L, 41L, 44L, 
118L, 121L, 125L, 127L, 132L, 134L, 148L, 149L, 179L, 182L, 194L, 
203L, 204L, 210L, 227L, 241L, 246L, 249L, 278L, 298L, 324L, 328L, 
364L, 370L, 380L, 383L, 397L, 405L, 427L, 443L, 450L, 453L, 454L, 
476L, 479L, 493L, 512L, 524L, 566L, 582L, 586L, 592L, 600L, 604L, 
619L, 633L, 638L, 641L, 650L, 657L, 659L, 661L, 663L, 674L, 676L, 
683L, 686L, 689L, 693L, 719L, 720L, 723L, 726L, 728L, 732L, 746L, 
748L, 752L, 757L, 762L, 768L, 769L, 783L, 785L, 789L, 795L, 811L, 
829L, 839L, 846L, 847L, 860L, 878L, 890L, 892L, 915L, 918L, 933L, 
948L, 976L, 986L, 987L, 1034L, 1040L, 1055L, 1061L, 1072L, 1081L, 
1085L, 1088L, 1091L, 1107L, 1113L, 1114L, 1115L, 1125L, 1135L, 
1140L, 1143L, 1144L, 1148L, 1155L, 1159L, 1161L, 1166L, 1168L, 
1175L, 1179L, 1186L, 1201L, 1222L, 1232L, 1234L, 1238L, 1241L, 
1249L, 1256L, 1262L, 1269L, 1378L, 1403L, 1417L, 1446L, 1447L, 
1489L, 1493L, 1498L, 1501L, 1504L, 1515L, 1521L, 1534L, 1545L, 
1563L, 1566L, 1587L, 1596L, 1597L, 1599L, 1600L, 1608L, 1618L, 
1631L, 1641L, 1653L, 1678L, 1690L, 1696L, 1700L, 1711L, 1718L, 
1737L, 1774L, 1778L, 1792L, 1793L, 1795L, 1806L, 1807L, 1811L, 
1820L, 1821L, 1822L, 1831L, 1835L, 1837L, 1846L, 1853L, 1854L, 
1875L, 1883L, 1884L, 1889L, 1895L, 1902L, 1907L, 1916L, 1920L, 
1927L, 1933L, 1939L, 1941L, 1957L, 1965L, 1973L, 1974L, 1977L, 
1991L, 2005L, 2032L, 2035L, 2048L, 2051L, 2062L, 2072L, 2103L, 
2113L, 2124L, 2126L, 2132L, 2150L, 2151L, 2173L, 2188L, 2195L, 
2202L, 2207L, 2210L, 2217L, 2218L, 2221L, 2224L, 2229L, 2240L, 
2244L, 2248L, 2259L, 2265L, 2301L, 2324L, 2333L, 2339L, 2340L, 
2352L, 2353L, 2358L, 2372L, 2376L, 2381L, 2384L, 2392L, 2413L, 
2426L, 2445L, 2451L, 2454L, 2455L, 2459L, 2460L, 2472L, 2478L, 
2484L, 2486L, 2490L, 2498L, 2515L, 2518L, 2525L, 2528L, 2532L, 
2551L, 2558L, 2568L, 2587L, 2608L, 2609L, 2618L, 2620L, 2621L, 
2630L, 2633L, 2670L, 2673L, 2683L, 2690L, 2696L, 2703L, 2705L, 
2712L, 2715L, 2718L, 2738L, 2740L, 2748L, 2749L, 2750L, 2768L, 
2772L, 2779L, 2794L, 2818L, 2826L, 2829L, 2838L), value = c(0.974683544303797, 
1, 1, 1, 1, 0.666666666666667, 1, 0.852941176470588, 1, 1, 1, 
0.928571428571429, 0.957446808510638, 0.952380952380952, 0.939024390243902, 
1, 1, 1, 1, 0.9375, 1, 0.75, 1, 0.932432432432432, 0.914893617021277, 
0.75, 0.883333333333333, 0.945098039215686, 0.911111111111111, 
1, 0.955223880597015, 0.972222222222222, 1, 1, 1, 0.692307692307692, 
0.932203389830508, 0.333333333333333, 1, 1, 0.882352941176471, 
0.818181818181818, 0.882352941176471, 1, 1, 1, 0.850574712643678, 
0.878787878787879, 1, 0.866666666666667, 1, 0.824742268041237, 
0.748148148148148, 1, 1, 1, 0.931034482758621, 0.96875, 1, 1, 
0.875, 1, 1, 1, 1, 0.666666666666667, 1, 1, 0.739130434782609, 
0.642857142857143, 0, 1, 1, 0.96875, 0.76, 0.747899159663866, 
0.888888888888889, 1, 0.948979591836735, 0.888888888888889, 1, 
1, 1, 1, 0.975609756097561, 1, 0.6875, 0.788235294117647, 0.9375, 
0.888888888888889, 1, 0.666666666666667, 1, 0.875, 1, 0.991111111111111, 
0.928571428571429, 1, 0.923076923076923, 1, 0.689922480620155, 
1, 0.684210526315789, 1, 0.779661016949153, 1, 1, 0.704545454545455, 
0.703703703703704, 1, 1, 1, 0, 0.655172413793103, 0.875, 1, 1, 
1, 0.7, 0.857142857142857, 1, 1, 0.686274509803922, 1, 1, 1, 
1, 0, 0.5, 1, 1, 0.995412844036697, 0.857142857142857, 0.75, 
0.75, 0.75, 0.5, 0.96, 0.693227091633466, 1, 0.5, 1, 1, 1, 1, 
1, 0.627906976744186, 0.666666666666667, 0.888888888888889, 0, 
0.75, 0.714285714285714, 0.8, 0.6, 0.444444444444444, 0.666666666666667, 
0.666666666666667, 0.416666666666667, 0.4, 0, 1, 1, 1, 0.975, 
1, 1, 1, 1, 0.994871794871795, 0.615384615384615, 1, 1, 0.538461538461538, 
0.714285714285714, 0.5, 1, 1, 1, 1, 1, 0.589285714285714, 0.384615384615385, 
1, 0.75, 1, 1, 0.5, 1, 1, 0.4, 1, 1, 1, 1, 0.578947368421053, 
1, 0.842105263157895, 0.714285714285714, 0.53125, 0.5, 0, 0.636363636363636, 
0.6, 0, 1, 1, 1, 1, 1, 0.888888888888889, 1, 1, 1, 1, 1, 0.888888888888889, 
0.24390243902439, 0.933333333333333, 0.5, 0.3125, 0.904761904761905, 
0.368421052631579, 0.307692307692308, 0.5, 0.5, 0.285714285714286, 
0.209302325581395, 0.857142857142857, 0.466666666666667, 0.5, 
1, 1, 0.216867469879518, 1, 0.147058823529412, 0.846153846153846, 
0.888888888888889, 1, 1, 1, 0.947368421052632, 1, 1, 0.9, 1, 
1, 1, 0.9375, 1, 1, 0.125, 1, 1, 0.454545454545455, 1, 0.111111111111111, 
1, 1, 1, 0.125, 0.230769230769231, 0.375, 1, 0, 0.333333333333333, 
0, 0, 0.142857142857143, 0.0697674418604651, 0.230769230769231, 
1, 1, 0.110497237569061, 0.142857142857143, 0.0714285714285714, 
0.166666666666667, 1, 0.051948051948052, 0.0888888888888889, 
0, 1, 0, 1, 1, 0.0833333333333333, 1, 1, 0.125, 0, 0.96875, 1, 
0.986111111111111, 1, 0.0909090909090909, 0, 0.888888888888889, 
0, 0, 0.608695652173913, 0)), class = c("tbl_df", "tbl", "data.frame"
), row.names = c(NA, -300L))

其中measurement_id只是每个度量值的唯一标识符，value是度量值本身（它碰巧在0和1之间，但不意味着概率意义，在其他情况下可以是任何数字）。

ggplot(data = my_measurements) + 
    geom_density(mapping = aes(x = value, ..density..))

它看起来像这样：

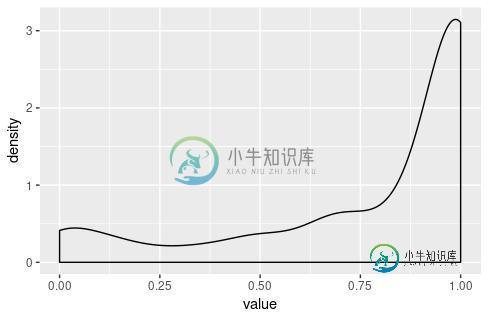
正如您所看到的，值的范围是0到1，但是很多值都接近1。

我的问题是：我如何使用曲线在情节中作为概率密度函数（我希望我使用的是正确的术语，如果不是请纠正我！）从？？？

希望这是有意义的，非常感谢你的帮助。

Answer 1

我想知道你为什么需要这个。也许你可以用bootstrap方法代替？

可以使用逆变换采样：

mysampler <- function(x, n) {
  y <- runif(n)
  c(quantile(x, probs = y)) #maybe a different quantile type should be used?
}
set.seed(42) #for reproducibility
sample <- mysampler(my_measurements$value, 500) #500 sampled values

#check
library(ggplot2)
ggplot() + 
  geom_density(data = my_measurements, aes(x = value, ..density..)) +
  geom_density(data = data.frame(value = sample), aes(x = value, ..density..), color = "red")

注意，所描述的核密度估计依赖于带宽。