2. 离散信源

我们已经看到，在非常一般的条件下，离散信道中可出现信号数的对数随时间线性增加。如果能给出这一增长速率，也就是每秒需要多少比特来表示所使用的特定信号，每秒钟所需要的比特数，就能给出信息传输容量。

我们现在考虑信源。如何用数学描述一个信源呢？一个给定信源每秒生成多少比特的信息呢？问题的要点在于，如何利用信源的相关统计知识，通过信息的正确编码，减少所需要的信道容量。比如，在电报通信中，要传送的消息由字符序列组成。但是，这些序列并不是完全随机的。一般情况下，它们会组成句子，具有某种语言的统计结构，比如英语。字符E的出现频率要高于Q，序列TH的出现频率要高于XP，等等。由于此种结构的存在，我们可以对消息序列进行适当编码，转换为信号序列，以节省时间（或信道容量）。其实在电报通讯中已经进行了一定程度的此种处理：为最常见的英文字母E使用最短的信道符号——点；而出现较少的Q，X，Z则使用较长的点、划序列来表示。这一思想一直沿用到一个特定的商用编码中，在这些编码中，常见的单词和短语用四字符或五字符代码组表示，大幅缩短了平均时间。现在使用的一些标准问候电报和周年纪念电报扩展了这一思想，将一个或两个句子编码为一个较短的数字序列。

我们可以认为离散信源是逐个字符地生成消息。它将会根据特定概率值选择相继符号，这些概率值通常取决于之前的选择和所考虑的特定符号。如果一个物理系统或者一个系统的数学模型，在一组概率的控制下生成符号序列，则这种系统或模型称为随机过程。因此，我们可以考虑用随机过程表示离散信源。相反，任何一个随机过程，只要它生成的离散符号序列是从有限集合中选出的，则可以将其看作离散信源。它将包括类似以下的各种情况：

1. 自然书写的语言，比如英文，德文，中文。

2. 已经用某种量化过程变为离散的连续信源。比如，由PCM发送器输出的量化语音，或者是经过量化的电视信号。

3. 数学信源，在此类情况下，我们只是抽象地定义了一个生成符号序列的随机过程。下面是最后一种信源类型的示例。

(A) 假定我们有五个字母A，B，C，D，E，各字母被选中的概率为0.2，前后选择之间相互独立。这样会得到一个序列，下面是其中的一个典型示例。

B D C B C E C C C A D C B D D A A E C E E A

A B B D A E E C A C E E B A E E C B C E A D

这一序列是使用一个随机数字表生成的。

(B) 使用相同的五个字母，设各概率为0.4，0.1，0.2，0.2，0.1，连续选择之间互相独立。则由这一信源生成的典型消息为：

A A A C D C B D C E A A D A D A C E D A

E A D C A B E D A D D C E C A A A A A D

(C) 如果相邻符号的选择不是独立的，其概率取决于之前的字符，则会得到一种更为复杂的结构。在最简单的此种类型中，字符的选择仅取决于它前面的一个字母，而与再之前的字母无关。这种统计结构可以由一组转换概率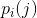来描述，该概率是指字母i之后跟有字母j的概率。下标i和j的取值范围为所有可能出现的符号。还有一种等价方式来指定该结构，即给出“连字(digram)”概率p(i, j)，也就是连字i j的相对频率。字母频率p(i)（即字母i的概率）、转换概率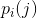和连字概率p(i, j)之间的关系由以下公式给出：

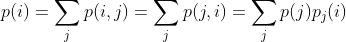
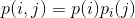
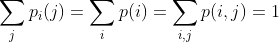
作为一个特定示例，假定共有三个字母A，B，C，其概率表为：

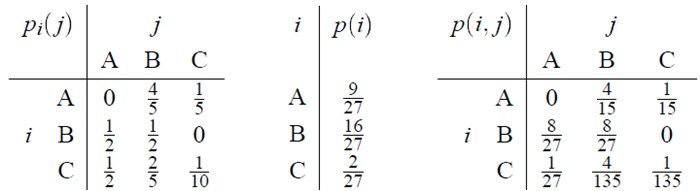
这一信源给出的一条典型消息如下：

A B B A B A B A B A B A B A B B B A B B B B B A B A B A B A B B B A C A C A B B A B B B B A B B A B A C B B B A B A。

接下来进一步提高复杂性，涉及三连字频率，但不涉及更多的连字频率。一个字母的选择取决于前面的两个字母，但与该点之前的消息无关。这里需要一组三连字频率p(i, j, k)，或者一组等价的转换概率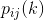。以这种方式继续下去，可以持续得到更为复杂的随机过程。在一般的n连字情况下，需要用一组n连字概率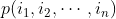或者转换概率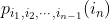来指定其统计结构。

(D) 还可以定义一些随机过程，它们生成由“单词”序列组成的文本。假定该语言中有五个字母A，B，C，D，E和16个“单词”，其相关概率为：

0.10 A 0.16 BEBE 0.11 CABED 0.04 DEB

0.04 ADEB 0.04 BED 0.05 CEED 0.15 DEED

0.05 ADEE 0.02 BEED 0.08 DAB 0.01 EAB

0.01 BADD 0.05 CA 0.04 DAD 0.05 EE

假定连续“单词”之间用空格分开，而且它们的选择相互独立。一条典型消息可能是：

DAB EE A BEBE DEED DEB ADEE ADEE EE DEB BEBE BEBE BEBE ADEE BED DEED DEED CEED ADEE A DEED DEED BEBE CABED BEBE BED DAB DEED ADEB。

如果所有单词的长度有限，则这一过程与前一种类型等价，但用单词结构和概率进行描述时，可能更简单一些。我们也可以进行推广，引入单词之间的转换概率，等等。

要构造一些简单的问题和示例来说明各种概率，这些虚拟语言是很有用的。我们还可以利用一系列简单的虚拟语言来模拟一种自然语言。如果所有字母的选择频率相同，且相互独立，则得到零阶近似。如果连续字母的选择相互独立，但每个字母的选择概率和它在自然语言中的概率相同，则得到一阶近似。于是，在英语的一阶近似中，选择E的概率为0.12（也就是它在正常英语中的出现概率），选择W的概率为0.02，但相邻字母之间没有影响，也不会倾向于生成自然语言中更频繁出现的二连字，比如TH、ED等。在二阶近似中，引入了两连字结构。在选定第一个字母后，根据各个字母在第一个字母之后的出现频率来选择下一个字母。这就是一个二连字频率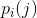表。在三阶近似中，引入了三连字结构。每个字母的选择概率依赖于它前面的两个字母。