25. 平均功率受限时的信道容量

定理16的一种简单应用情景是：噪声为白色热噪声，传送信号的平均功率不超过P。则接收信号的平均功率为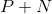，其中N是平均噪声功率。当接收信号也构成一个白噪声系集时，接收信号的熵最大，因为这是功率为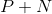时的最大可能熵，通过适当选择传送信号，也就是在使其构成一个功率为P的白噪声系集时，可以获得这一最大值。接收系集的熵（每秒）为：

，

噪声熵为：

。

信道容量为：

。

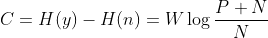综述如下：

定理17：当平均传送功率不超过P，带宽为W的信道受功率为N的白色热噪声干扰时，其信道容量为：

。

这意味着，通过足够复杂的编码系统，能够以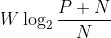比特/秒的速率传送二进制数位，使错误频率为任意小。任何编码系统在以更高速率传送信息时，都会使错误频率高于某个确定的正值。

为了接近这一极限传送速率，传送信号的统计性质必须接近于白噪声。下面介绍一种可以趋近于理想速率的系统：假设有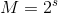个白噪声样本，每个持续时间为T。为它们分配0至M-1的二进制数字。在传送机将这些消息序列分为s个组，对于每一组为说，相应的噪声样本被作为信号传送。在接收端，已知M个样本，并将实际接收信号（受噪声干扰）与所有这些样本对比。与接收信号的RMS最小的样本被选作传送信号，并重建相应的二进制数字。这一过程用于选择可能性最大的信号（后验概率）。所使用的噪声样本数M将取决于可容忍的错误频率，但几乎所有不同的样本选择，都有：

，

使得无论选择多么小的，总是可以选择足够大的T，在时间T内传送的二进位任意接近。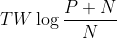

对于白噪声情况，其他几位作者已经独立地推导出类似于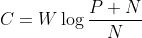的公式，只是其解释有所不同。我们会提到N. Wiener、W. G. Tuller和H. Sullivan在这方面的工作。

当干扰噪声为任意噪声时（不一定为白色热噪声），似乎无法显式解决信道容量C的最大化问题。但是，可以用平均噪声功率N和噪声熵功率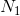为C设定上、下限。在大多数实际情况下，这些限制足够接近，从而给出该问题的一个令人满意的答案。

定理18：一个信道的带宽为W，受任意噪声的干扰，其容量满足以下不等式：

其中：

P=平均传送功率
N=平均噪声功率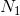
=噪声的熵功率。

受干扰信号的平均功率同样为P+N。当接收信号为白噪声时，得到这一功率的最大熵，即。这是不可能实现的；也就是说，对于传送信号的任意系集，与干扰噪声叠加在一起后，都不会在接收端生成一个白色热噪声，但至少它为H(y)设定了上限。因此可得：

.

这就是定理中给出的上限。如果传送信号是功率为P的白噪声，考虑其传送速率就可以得到下限。在这种情况下，接收信号的熵功率至少和功率为的白噪声的熵功率一样大，这是因为，我们在前面的定理中已经证明，两个系集之和的熵功率大于或等于各个熵功率之和。因此：

及

当P增大时，上下限相互接近，所以可以得到一个近似速率：

如果噪声本身是白色的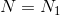，，则该结果简化为前面证明的公式：

如果噪声是高斯噪声，但其频谱不一定是平坦的，则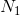是该噪声功率在频带W中各频率上的几何均值。因此，

其中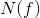，是在频率f处的噪声功率。

定理19：如果对于给定传送功率P的信道，设定其容量为：

，

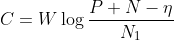则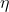随着P的增大而单调递减，并趋近于极限0。

假定对于一个给定功率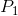，信道容量为：

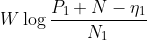
这意味着在将最佳信号分布（比如说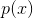）加到噪声分布上时，会得出熵功率为的接收信号分布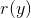。假定我们向信号加上一个功率为的白噪声，从而将该功率增加到。针对和的最小熵功率应用该定理，可以得出接收信号的熵至少为：

因此，由于我们可以得到上述H，所以最大化分布的熵必然至少一样大，而且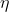必然为单调递减的。要证明当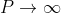时，可考虑一个信号，它是功率P很大的白噪声。如果P足够大，无论干扰噪声如何，接收到信号都近似为一个白噪声，也就是说他的熵功率接近于P+N。