26. 峰值功率受限时的信道容量
在某些应用中,传送器受到的限制不是平均功率而是瞬时峰值功率。信道容量的计算问题于是就变成了:系集中的所有函数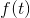 对于所有t都小于或等于
对于所有t都小于或等于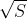 ,在此条件下,如何(通过改变所传送符号的系集)使下式取最大值:
,在此条件下,如何(通过改变所传送符号的系集)使下式取最大值:
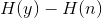
这种约束条件无法像平均功率限制那样很好地以数学方式给出。对于这种情景,我们最多获得一个对于所有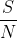 有效的下限,一个“渐近”上限(对于大的
有效的下限,一个“渐近”上限(对于大的 有效)和当
有效)和当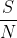 较小时的渐近C值。
较小时的渐近C值。
定理20:一个信道的带宽为W,受功率为N的白色热噪声干扰,则其信道容量的下限为:
其中,S是允许传送的峰值功率。对于足够大的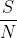 ,有:
,有:
其中 为任意小。当
为任意小。当时(假定频带W的起点频率为0)
我们希望使接收信号的熵取最大值。如果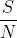 很大,则近似在使传送系集的熵最大时,接收信号的熵取最大值。
很大,则近似在使传送系集的熵最大时,接收信号的熵取最大值。
放松对系集的条件,可以获得渐近的上限。假定该功率不是在每个时刻受限于S,而只是在样本点处受限。在这一弱化条件下,所传送系集的最大熵当然大于或等于在原条件下的最大熵。这个经过修改的问题很容易求解。如果不同的样本点相互独立的,而且有一个在从 到
到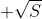 范围内为常数的分布,即可得到最大熵。这个熵值可计算如下:
范围内为常数的分布,即可得到最大熵。这个熵值可计算如下:
。
于是接收信号的熵将小于:
其中,当时,
,减去白噪声的熵(
),即可得到信道容量:
。
这就是我们想要的信道容量上限。
为获得下限,考虑同一函数系集。让这些函数传送一个具有三角传输特性的理想滤波器。其增益在频率0处为单位1,然后线性下降,在频率W处的增益为0。我们首先证明滤波器的输出函数在所有时间内(而不是取样点)的峰值功率上限为S。首先注意到脉冲进入滤波器后,在输出端得到:
此函数永远不会为负值。一般情况下的输入函数可以看作是一系列如下函数之和:
其中a为样本的函数,不大于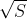 。因此,输出也是上述非负形式的移位函数之和,且系数相同。这些函数是非负的,所以当所有系数a取其最大正值(即
。因此,输出也是上述非负形式的移位函数之和,且系数相同。这些函数是非负的,所以当所有系数a取其最大正值(即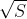 )时,获得对于任意时间t的最大正值。在这种情况下,输入函数为一个幅度为
)时,获得对于任意时间t的最大正值。在这种情况下,输入函数为一个幅度为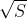 的常数,由于对于直流而言,该滤波器的增益为单位1,所以输出也相同。因此,输出系集的峰值功率为S。
的常数,由于对于直流而言,该滤波器的增益为单位1,所以输出也相同。因此,输出系集的峰值功率为S。
利用适用于这一情景的定理,由输入系集的熵可以计算出输出系集的熵。输出熵等于输入熵加上滤波器的几何平均值:
因此,输出熵为:
信道容量大于:
。
我们现在希望证明:对于小的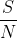 (峰值信号功率除以平均白噪声功率),则信道容量近似为:
(峰值信号功率除以平均白噪声功率),则信道容量近似为:
更准确地说,当时,
。由于平均信号功率P小于或等于峰值功率S,则可以得出,对于所有
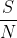 :
:
因此,如果可以找到一个函数系集,近似对应于,且受限于带宽W和峰值功率S,则可以证得结果。考虑以下类型的函数系集。t个采样的值相同,或者为
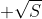 或
或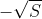 ,接下来的t个采样也具有相同值,以此类推。一个系列的取值为随机选定,以概率
,接下来的t个采样也具有相同值,以此类推。一个系列的取值为随机选定,以概率 取
取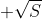 ,以概率
,以概率 取
取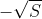 。如果将这一系集通过具有三角增益特性的滤波器(对于直流为单位增益),则输入的峰值功率限于
。如果将这一系集通过具有三角增益特性的滤波器(对于直流为单位增益),则输入的峰值功率限于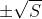 。此外,平均功率近似为S,取足够大的t值,即可趋近于该值。应用关于噪声与小信号之和的定理,可以求出这一系集与热噪声之和的熵。如果
。此外,平均功率近似为S,取足够大的t值,即可趋近于该值。应用关于噪声与小信号之和的定理,可以求出这一系集与热噪声之和的熵。如果
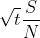 足够小,这一定理将适用。(在选定t之后)取
足够小,这一定理将适用。(在选定t之后)取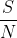 足够小,可以确保满足这一条件。熵功率将任意接近于S+N,因此,传送速率将任意接近于
足够小,可以确保满足这一条件。熵功率将任意接近于S+N,因此,传送速率将任意接近于

