实时时序数据中的峰值信号检测

Question

更新：到目前为止，性能最好的算法就是这个。

这个问题探索了检测实时时间序列数据中突然峰值的鲁棒算法。

考虑下面的示例数据：

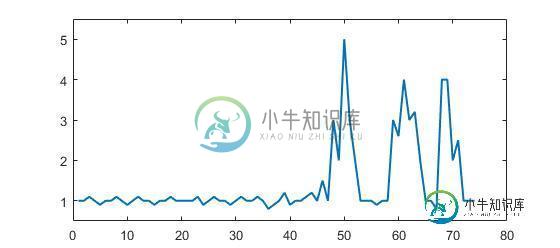
_{此数据的示例为Matlab格式（但此问题与语言无关，而与算法有关）：}

p = [1 1 1.1 1 0.9 1 1 1.1 1 0.9 1 1.1 1 1 0.9 1 1 1.1 1 1 1 1 1.1 0.9 1 1.1 1 1 0.9, ...
     1 1.1 1 1 1.1 1 0.8 0.9 1 1.2 0.9 1 1 1.1 1.2 1 1.5 1 3 2 5 3 2 1 1 1 0.9 1 1, ... 
     3 2.6 4 3 3.2 2 1 1 0.8 4 4 2 2.5 1 1 1];

你可以清楚地看到有三个大峰和一些小峰。此数据集是问题所涉及的timeseries数据集类的一个特定示例。此类数据集具有两个一般特征：

1. 存在具有一般平均值的基本噪声
2. 存在明显偏离噪声的大“峰值”或“更高数据点”

我们还假设以下情况：

• 峰的宽度无法事先确定

对于这种情况，需要构造触发信号的边界值。但是，边界值不能是静态的，必须根据算法实时确定。

我的问题是：什么是实时计算此类阈值的好算法？有针对这种情况的特定算法吗？最著名的算法是什么？

_{稳健的算法或有用的见解都受到高度赞赏。（可以用任何语言回答：关于算法）}

Answer 1

一种方法是根据以下观察结果检测峰值：

• 时间t是峰值，如果（y（t）

它通过等待上升趋势结束来避免误报。它不完全是“实时”的，因为它将错过峰值1 dt。灵敏度可以通过要求比较裕度来控制。噪声检测和检测延时之间存在折衷。可以通过添加更多参数来丰富模型：

• 峰值if（y（t）-y（t-dt）

其中，dt和m是控制灵敏度与时间延迟的参数

以下是用python重现绘图的代码：

import numpy as np
import matplotlib.pyplot as plt
input = np.array([ 1. ,  1. ,  1. ,  1. ,  1. ,  1. ,  1. ,  1.1,  1. ,  0.8,  0.9,
    1. ,  1.2,  0.9,  1. ,  1. ,  1.1,  1.2,  1. ,  1.5,  1. ,  3. ,
    2. ,  5. ,  3. ,  2. ,  1. ,  1. ,  1. ,  0.9,  1. ,  1. ,  3. ,
    2.6,  4. ,  3. ,  3.2,  2. ,  1. ,  1. ,  1. ,  1. ,  1. ])
signal = (input > np.roll(input,1)) & (input > np.roll(input,-1))
plt.plot(input)
plt.plot(signal.nonzero()[0], input[signal], 'ro')
plt.show()

Answer 2

下面是平滑z-score算法的Python/numpy实现（参见上面的答案）。你可以在这里找到要点。

#!/usr/bin/env python
# Implementation of algorithm from https://stackoverflow.com/a/22640362/6029703
import numpy as np
import pylab

def thresholding_algo(y, lag, threshold, influence):
    signals = np.zeros(len(y))
    filteredY = np.array(y)
    avgFilter = [0]*len(y)
    stdFilter = [0]*len(y)
    avgFilter[lag - 1] = np.mean(y[0:lag])
    stdFilter[lag - 1] = np.std(y[0:lag])
    for i in range(lag, len(y)):
        if abs(y[i] - avgFilter[i-1]) > threshold * stdFilter [i-1]:
            if y[i] > avgFilter[i-1]:
                signals[i] = 1
            else:
                signals[i] = -1

            filteredY[i] = influence * y[i] + (1 - influence) * filteredY[i-1]
            avgFilter[i] = np.mean(filteredY[(i-lag+1):i+1])
            stdFilter[i] = np.std(filteredY[(i-lag+1):i+1])
        else:
            signals[i] = 0
            filteredY[i] = y[i]
            avgFilter[i] = np.mean(filteredY[(i-lag+1):i+1])
            stdFilter[i] = np.std(filteredY[(i-lag+1):i+1])

    return dict(signals = np.asarray(signals),
                avgFilter = np.asarray(avgFilter),
                stdFilter = np.asarray(stdFilter))

下面是对相同数据集的测试，该数据集产生了与原始答案中相同的情节

# Data
y = np.array([1,1,1.1,1,0.9,1,1,1.1,1,0.9,1,1.1,1,1,0.9,1,1,1.1,1,1,1,1,1.1,0.9,1,1.1,1,1,0.9,
       1,1.1,1,1,1.1,1,0.8,0.9,1,1.2,0.9,1,1,1.1,1.2,1,1.5,1,3,2,5,3,2,1,1,1,0.9,1,1,3,
       2.6,4,3,3.2,2,1,1,0.8,4,4,2,2.5,1,1,1])

# Settings: lag = 30, threshold = 5, influence = 0
lag = 30
threshold = 5
influence = 0

# Run algo with settings from above
result = thresholding_algo(y, lag=lag, threshold=threshold, influence=influence)

# Plot result
pylab.subplot(211)
pylab.plot(np.arange(1, len(y)+1), y)

pylab.plot(np.arange(1, len(y)+1),
           result["avgFilter"], color="cyan", lw=2)

pylab.plot(np.arange(1, len(y)+1),
           result["avgFilter"] + threshold * result["stdFilter"], color="green", lw=2)

pylab.plot(np.arange(1, len(y)+1),
           result["avgFilter"] - threshold * result["stdFilter"], color="green", lw=2)

pylab.subplot(212)
pylab.step(np.arange(1, len(y)+1), result["signals"], color="red", lw=2)
pylab.ylim(-1.5, 1.5)
pylab.show()

Answer 3

我想出了一个非常适合这些类型数据集的算法。它基于分散原理：如果一个新的数据点是给定的远离某个移动均值的x个标准偏差，则算法发出信号（也称为z分数）。该算法非常鲁棒，因为它构造了单独的移动均值和偏差，使得信号不会破坏阈值。因此，无论先前信号的数量如何，未来信号的识别精度大致相同。该算法需要3个输入：延迟=移动窗口的延迟，阈值=算法信号和影响=新信号对均值和均值的影响（在0和1之间）方差.例如，5的延迟将使用最后5个观察结果来平滑数据。如果数据点距离移动均值有3.5个标准偏差，则3.5的阈值将发出信号。0.5的影响给信号的影响是正常数据点的一半。同样，0的影响完全忽略重新计算新阈值的信号。因此，0的影响是最稳健的选项（但假设稳定）；将影响选项设置为1是最不稳健的。因此，对于非平稳数据，影响选项应该放在0和1之间。

其工作原理如下：

伪码

# Let y be a vector of timeseries data of at least length lag+2
# Let mean() be a function that calculates the mean
# Let std() be a function that calculates the standard deviaton
# Let absolute() be the absolute value function

# Settings (the ones below are examples: choose what is best for your data)
set lag to 5;          # lag 5 for the smoothing functions
set threshold to 3.5;  # 3.5 standard deviations for signal
set influence to 0.5;  # between 0 and 1, where 1 is normal influence, 0.5 is half

# Initialize variables
set signals to vector 0,...,0 of length of y;   # Initialize signal results
set filteredY to y(1),...,y(lag)                # Initialize filtered series
set avgFilter to null;                          # Initialize average filter
set stdFilter to null;                          # Initialize std. filter
set avgFilter(lag) to mean(y(1),...,y(lag));    # Initialize first value
set stdFilter(lag) to std(y(1),...,y(lag));     # Initialize first value

for i=lag+1,...,t do
  if absolute(y(i) - avgFilter(i-1)) > threshold*stdFilter(i-1) then
    if y(i) > avgFilter(i-1) then
      set signals(i) to +1;                     # Positive signal
    else
      set signals(i) to -1;                     # Negative signal
    end
    set filteredY(i) to influence*y(i) + (1-influence)*filteredY(i-1);
  else
    set signals(i) to 0;                        # No signal
    set filteredY(i) to y(i);
  end
  set avgFilter(i) to mean(filteredY(i-lag+1),...,filteredY(i));
  set stdFilter(i) to std(filteredY(i-lag+1),...,filteredY(i));
end

为您的数据选择良好参数的经验法则可以在下面找到。

_{这个演示的Matlab代码可以在这里找到。要使用演示，只需运行它，并通过单击上面的图表自己创建一个时间序列。算法开始工作后绘制滞后观察数。}

对于原始问题，当使用以下设置时，此算法将给出以下输出：lag=30，threshold=5，influence=0：

• Matlab（me）

• R（me）

• Golang（XeonCross）

• 蟒蛇（R Kiselev）

• Python[高效版本]（delica）

• 斯威夫特（我）

• Groovy（JoShuaCWebDeveloper）

• C（brad）

• C（动画潘迪）

• Rust（swizard）

• 斯卡拉（迈克·罗伯茨）

• 静态编程语言

  鲁比（金莫·莱托）

  Fortran[用于共振检测]（THo）

  朱莉娅（马特·坎普）

  C#（海洋空投）

  C（DavidC）

  Java（takanuva15）

  JavaScript（Dirk Lüsebrink）

  TypeScript（Jerry Gamble）

  Perl（Alen）

  PHP（radhoo）

  PHP（gtjamesa）

  飞镖（sga）

lag：lag参数确定数据平滑程度以及算法对数据长期平均值变化的适应性。数据越平稳，应该包含的滞后就越多（这将提高算法的鲁棒性）。如果您的数据包含随时间变化的趋势，那么您应该考虑快速算法适应这些趋势的速度。也就是说，如果将lag设置为10，则需要10个“周期”才能将算法的treshold调整为长期平均值的任何系统性变化。因此，根据数据的趋势行为和算法的自适应程度选择lag参数。

影响：此参数确定信号对算法检测阈值的影响。如果设置为0，则信号对阈值没有影响，从而基于使用不受过去信号影响的平均值和标准偏差计算的阈值来检测未来信号。如果设置为0.5，信号的影响只有正常数据点的一半。考虑这一点的另一种方式是，如果将影响值设置为0，则隐含地假定平稳性（即，无论有多少信号，您始终希望时间序列在长期内返回到相同的平均值）。如果情况并非如此，则应将影响参数置于0和1之间的某个位置，这取决于信号系统地影响数据时变趋势的程度。例如，如果信号导致时间序列长期平均值的结构性中断，则应将影响参数设置为高（接近1），以便阈值能够对结构性中断做出快速反应。

threshold：threshold参数是移动平均值的标准偏差数，在移动平均值以上，算法将新数据点分类为信号。例如，如果一个新的数据点比移动平均值高4.0个标准差，且阈值参数设置为3.5，则算法将该数据点识别为信号。此参数应根据您期望的信号数量进行设置。例如，如果您的数据是正态分布的，则3.5的阈值（或：z分数）对应于0.00047的信令概率（从该表中），这意味着您期望每2128个数据点（1/0.00047）发送一次信号。因此，阈值直接影响算法的灵敏度，并由此确定算法发送信号的频率。检查您自己的数据，并选择一个合理的阈值，使算法在需要时发出信号（这里可能需要一些尝试和错误，以获得适合您的目的的好阈值）。

警告：上述代码每次运行时都会在所有数据点上循环。实现此代码时，请确保将信号的计算拆分为单独的函数（不带循环）。然后，当新数据点到达时，更新filteredY、avgFilter和stdFilter一次。不要每次有新的数据点（如上面的示例）时都重新计算所有数据的信号，这在实时应用程序中效率极低且速度很慢。

修改算法的其他方法（潜在改进）包括：

1. 使用中位数而不是平均值

>

里科夫，Y.，塔赫，T.Q.，博吉克，I.，克里斯托普洛斯，G。，

Hong，Y.，Xin，Y.，Martin，H.，Bucher，D。，

Grammenos， A.， Kalyvianaki， E.，

科蒂亚尔，N.（2020年）。融合图像多通道辅助心脏电生理过程。雷恩大学博士论文。

贝克曼，W.F.，吉姆·内兹，M。L.，莫尔兰，P.D.，威斯特霍夫，H.V。，

奥尔霍夫斯基，M.，穆勒洛娃，E。，

[1]高，

陈，G。

右高桥、M.福本、C.汉、T.佐佐谷、Y.纳如泽、。，

内格斯，M.J.，摩尔，M.R.，奥利弗，J.M.，西米埃努，R.（2020年）。液滴撞击Spring支撑板：分析和模拟。工程数学杂志，128（3）。

尹，C.（2020年）。冠状病毒SARS-CoV-2基因组中的二核苷酸重复：进化意义。ArXiv电子打印，可从以下网址访问：https://arxiv.org/pdf/2006.00280.pdf

Esnaola Gonzalez，I.，Gómez Omella，M.，Ferreiro，S.，Fernandez，I.，Lázaro，I。，

[1]高，

云，B.，塔林，B.，刘，A.，谢德，T.，林，X.，哈伯德，M.，...

Ceyssens， F.， Carmona， M. B.， Kil， D.， Deprez， M.， Tooten， E.， Nuttin， B.，...

Dons， E.， Laereman， M.， Orjuela， J.P.， Avila-Palencia， I.， de Nazelle， A.， Nieuwenhuijsen， M.，...

Schaible B.J.，Snook K.R.，Yin J.，等人（2019年）。2014年1月至2015年4月，五个不同国家关于脊髓灰质炎的推特对话和英语新闻媒体报道。《永久杂志》，23，18-181页。

利马，B.（2019年）。使用触觉机器人指尖探索物体表面（渥太华大学/渥太华大学博士论文）。

利马，B.M.R.，拉莫斯，L.C.S.，德奥利维拉，T.E.A.，达丰塞卡，V.P。，

利马，B.M.R.，德奥利维拉，T.E.A.，达丰塞卡，V.P.，朱，Q.，古布兰，M.，格罗扎，V.Z。，

丁，C.，菲尔德，R.，夸克，T.，鲍尔，T.（2019）。使用基于压缩的分析的广义边界检测。ICASSP 2019-2019 IEEE声学、语音和信号处理国际会议（ICASSP），英国布莱顿，第3522-3526页。

开利，E. E.（2019）。利用压缩求解离散线性系统。博士论文，伊利诺伊大学香槟分校。

Khandakar， A.， Chowdhury， M. E.， Ahmed， R.， Dhib， A.， Mohammed， M.， Al-Emadi， N.A.，

巴斯科佐斯，G.，道斯，J.M.， Austin， J.S.，安图内斯-马丁斯，A.，麦克德莫特，L.，克拉克，A. J.，...

云，B.，塔里恩，B.，克劳福德，R.，

Zajdel，T.J.（2018）。用于细菌生物传感的电子接口。博士论文，加州大学伯克利分校。

Perkins，P.，Heber，S.（2018年）。使用基于Z评分的峰值检测算法识别核糖体暂停位点。IEEE第八届生物和医学计算进展国际会议（ICCABS），ISBN:978-1-5386-8520-4。

摩尔，J.，戈芬，P.，迈耶，M.，伦德里根，P.，帕特瓦里，N.，斯沃德，K.，

Lo，O.，Buchanan，W.J.，Griffiths，P.，和Macfarlane，R.（2018），《改进内部威胁检测、安全和通信网络的距离测量方法》，第2018卷，文章ID 5906368。

Apurupa， N.V.， Singh， P.， Chakravarthy， S.，

Sciura， M.（2017）。情感音乐生成及其对玩家体验的影响。博士论文，哥本哈根IT大学，数字设计。

Scirea，M.，Eklund，P.，Togelius，J。，

Catalbas，M.C.，Cegovnik，T.，Sodnik，J.和Gulten，A.（2017）。基于眼跳运动的驾驶员疲劳检测，第十届电气和电子工程国际会议（ELECO），第913-917页。

其他作品使用的算法从这个答案

>

Bergamini，E.和E. Mourlon-Druol（2021）。谈欧洲：探索新闻档案70年。工作文件04/2021， Bruegel。

Cox， G.（2020）。测量信号中的峰值检测。关于https://www.baeldung.com/cs/signal-peak-detection.的在线文章

贝尔纳迪博士（2019年）。通过多模式手势将智能手表与移动设备配对的可行性研究。阿尔托大学硕士论文。

Lemmens，E.（2018年）。利用统计方法对事件日志中的异常值进行检测，硕士论文，埃因霍温大学。

Willems，P.（2017）。老年人情绪控制的情感氛围，硕士论文，屯特大学。

Ciocirdel，G.D.和Varga，M.（2016）。基于维基百科页面浏览量的选举预测。项目文件，阿姆斯特丹弗里吉大学。

从这个答案可以看出该算法的其他应用

>

用OpenBCI系统合成语音，SarahK01。

Python软件包：机器学习金融实验室，基于De Prado，M.L.（2018）的工作。金融机器学习的进展。约翰威利

Adafruit图书馆、Adafruit董事会（Adafruit Industries）

步进跟踪算法，Android应用程序（jeeshnair）

R套装：动物猎手（乔·冠军，西娅·苏基安托）

链接到其他峰值检测算法

• 噪声正弦时间序列中的实时峰值检测

Brakel，J.P.G.van（2014年）。“使用z分数的鲁棒峰值检测算法”。堆栈溢出。网址：https://stackoverflow.com/questions/22583391/peak-signal-detection-in-realtime-timeseries-data/22640362#22640362 （版本：2020-11-08）。

如果您在某个地方使用此功能，请使用上述参考来信任我。如果你对算法有任何疑问，请在下面的评论中发表，或者在LinkedIn上与我联系。