噪声正弦时间序列中的实时峰值检测

Question

我一直试图实时检测正弦时间序列数据中的峰值，但迄今为止没有成功。我似乎找不到一种能够以合理的精度检测正弦信号峰值的实时算法。我要么没有检测到峰值，要么正弦波上有无数个点被检测为峰值。

对于类似正弦波且可能包含一些随机噪声的输入信号，什么是好的实时算法？

作为一个简单的测试案例，考虑一个稳定的正弦波，它总是相同的频率和振幅。（确切的频率和振幅并不重要；我任意选择了60赫兹的频率，振幅为/−

dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
x  = sin(2*pi*60*t);

使用Jean Paul开发和发布的算法，我要么没有检测到峰值（左），要么检测到无数“峰值”（右）：

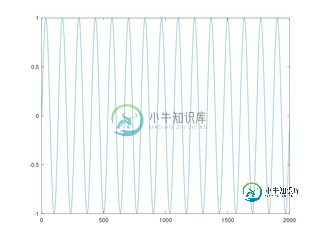
按照让-保罗给出的“经验法则”，我已经尝试了我能想到的这三个参数的几乎每一个值组合，但是到目前为止我还没有得到我预期的结果。

我发现了一个由Eli Billauer开发和发布的替代算法，它确实给了我想要的结果，例如：

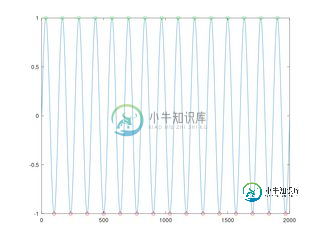
尽管Eli Billauer的算法简单得多，并且能够可靠地产生我想要的结果，但它不适合实时应用。

作为信号的另一个例子，我想应用这样的算法，考虑Eli Billauer为自己的算法给出的测试用例：

t = 0:0.001:10;
x = 0.3*sin(t) + sin(1.3*t) + 0.9*sin(4.2*t) + 0.02*randn(1, 10001);

这是一种更不寻常（不太均匀/规则）的信号，具有不同的频率和振幅，但通常仍为正弦信号。绘制时，峰值显而易见，但很难用算法识别。

正确识别正弦输入信号峰值的良好实时算法是什么？在信号处理方面，我并不是一个专家，因此有必要考虑一些正弦输入的经验法则。或者，也许我需要修改Jean-Paul的算法本身，以便正确处理正弦信号。如果是这样，需要做哪些修改，我将如何着手进行这些修改？

Answer 1

考虑使用find峰值，它速度很快，这对实时可能很重要。你应该过滤高频噪声以提高准确性。这里我用移动窗口平滑数据。

t = 0:0.001:10;
x = 0.3*sin(t) + sin(1.3*t) + 0.9*sin(4.2*t) + 0.02*randn(1, 10001);
[~,iPeak0] = findpeaks(movmean(x,100),'MinPeakProminence',0.5);

您可以为该过程计时（0.0015秒）

f0 = @() findpeaks(movmean(x,100),'MinPeakProminence',0.5)
disp(timeit(f0,2))

相比之下，处理斜率只快一点（0.00013秒），但FindPeak有许多有用的选项，例如峰值之间的最小间隔等。

iPeaks1 = derivePeaks(x);
f1 = @() derivePeaks(x)
disp(timeit(f1,1))

派生峰在哪里：

function iPeak1 = derivePeaks(x)
xSmooth = movmean(x,100);
goingUp = find(diff(movmean(xSmooth,100)) > 0);
iPeak1 = unique(goingUp([1,find(diff(goingUp) > 100),end]));
iPeak1(iPeak1 == 1 | iPeak1 == length(iPeak1)) = [];
end

Answer 2

如果你的正弦波不包含任何噪声，你可以使用一种非常经典的信号处理技术：取一阶导数，当它等于零时进行检测。

例如：

function signal = derivesignal( d )

% Identify signal
signal = zeros(size(d));
for i=2:length(d)
    if d(i-1) > 0 && d(i) <= 0
        signal(i) = +1;     % peak detected
    elseif d(i-1) < 0 && d(i) >= 0
        signal(i) = -1;     % trough detected
    end
end

end

使用您的示例数据：

% Generate data
dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
y  = sin(2*pi*60*t);

% Add some trends
y(1:1000) = y(1:1000) + 0.001*(1:1000)';
y(1001:2000) = y(1001:2000) - 0.002*(1:1000)';

% Approximate first derivative (delta y / delta x)
d = [0; diff(y)];

% Identify signal
signal = derivesignal(d);

% Plot result
figure(1); clf; set(gcf,'Position',[0 0 677 600])
subplot(4,1,1); hold on;
title('Data');
plot(t,y);
subplot(4,1,2); hold on;
title('First derivative');
area(d);
ylim([-0.05, 0.05]);
subplot(4,1,3); hold on;
title('Signal (-1 for trough, +1 for peak)');
plot(t,signal); ylim([-1.5 1.5]);
subplot(4,1,4); hold on;
title('Signals marked on data');
markers = abs(signal) > 0;
plot(t,y); scatter(t(markers),y(markers),30,'or','MarkerFaceColor','red');

这将产生：

这种方法对于任何类型的正弦波都非常有效，唯一的要求是输入信号不含噪声。

一旦输入信号包含噪声，导数方法就会失败。例如：

% Generate data
dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
y  = sin(2*pi*60*t);

% Add some trends
y(1:1000) = y(1:1000) + 0.001*(1:1000)';
y(1001:2000) = y(1001:2000) - 0.002*(1:1000)';

% Add some noise
y = y + 0.2.*randn(2000,1);

现在将生成此结果，因为第一个差异会放大噪声：

现在有很多处理噪声的方法，最标准的方法是应用移动平均滤波器。移动平均线的一个缺点是它们适应新信息的速度很慢，这样信号在发生后就可以被识别出来（移动平均线有滞后）。

另一种非常典型的方法是使用傅里叶分析来识别输入数据中的所有频率，忽略所有低振幅和高频正弦波，并使用剩余的正弦波作为滤波器。剩余的正弦波将（很大程度上）从噪声中清除，然后您可以再次使用第一差分来确定波峰和波谷（或者对于单个正弦波，您知道波峰和波谷发生在相位的1/4和3/4 pi处）。我建议你拿起任何信号处理理论书来学习更多关于这种技术的知识。matlab也有一些关于这方面的教育材料。

如果您想在硬件中使用此算法，我建议您也看看WFLC（加权傅里叶线性组合器），例如1个振荡器或PLL（锁相环），它可以在不进行完全快速傅里叶变换的情况下估计噪声波的相位。你可以在维基百科上找到锁相环的Matlab算法。

我将在这里建议一种稍微复杂一点的方法，它将实时识别波峰和波谷：使用移动最小二乘最小化和傅里叶分析的初始估计，将正弦波函数拟合到您的数据中。

这是我的功能：

function [result, peaks, troughs] = fitsine(y, t, eps)

% Fast fourier-transform
f = fft(y);
l = length(y);
p2 = abs(f/l);
p1 = p2(1:ceil(l/2+1));
p1(2:end-1) = 2*p1(2:end-1);
freq = (1/mean(diff(t)))*(0:ceil(l/2))/l;

% Find maximum amplitude and frequency
maxPeak = p1 == max(p1(2:end)); % disregard 0 frequency!
maxAmplitude = p1(maxPeak);     % find maximum amplitude
maxFrequency = freq(maxPeak);   % find maximum frequency

% Initialize guesses
p = [];
p(1) = mean(y);         % vertical shift
p(2) = maxAmplitude;    % amplitude estimate
p(3) = maxFrequency;    % phase estimate
p(4) = 0;               % phase shift (no guess)
p(5) = 0;               % trend (no guess)

% Create model
f = @(p) p(1) + p(2)*sin( p(3)*2*pi*t+p(4) ) + p(5)*t;
ferror = @(p) sum((f(p) - y).^2);
% Nonlinear least squares
% If you have the Optimization toolbox, use [lsqcurvefit] instead!
options = optimset('MaxFunEvals',50000,'MaxIter',50000,'TolFun',1e-25);
[param,fval,exitflag,output] = fminsearch(ferror,p,options);

% Calculate result
result = f(param);

% Find peaks
peaks = abs(sin(param(3)*2*pi*t+param(4)) - 1) < eps;

% Find troughs
troughs = abs(sin(param(3)*2*pi*t+param(4)) + 1) < eps;

end

如您所见，我首先执行傅里叶变换，以找到数据振幅和频率的初始估计值。然后，我使用模型a b sin（ct d）et将正弦波拟合到数据中。拟合值表示正弦波，我知道1和-1分别是峰值和波谷。因此，我可以将这些值识别为信号。

这对于具有（缓慢变化的）趋势和一般（白色）噪声的正弦曲线非常有效：

% Generate data
dt = 1/8000;
t  = (0:dt:(1-dt)/4)';
y  = sin(2*pi*60*t);

% Add some trends
y(1:1000) = y(1:1000) + 0.001*(1:1000)';
y(1001:2000) = y(1001:2000) - 0.002*(1:1000)';

% Add some noise
y = y + 0.2.*randn(2000,1);

% Loop through data (moving window) and fit sine wave
window = 250;   % How many data points to consider
interval = 10;  % How often to estimate
result = nan(size(y));
signal = zeros(size(y));
for i = window+1:interval:length(y)
    data = y(i-window:i);   % Get data window
    period = t(i-window:i); % Get time window
    [output, peaks, troughs] = fitsine(data,period,0.01);
    
    result(i-interval:i) = output(end-interval:end);
    signal(i-interval:i) = peaks(end-interval:end) - troughs(end-interval:end);
end

% Plot result
figure(1); clf; set(gcf,'Position',[0 0 677 600])
subplot(4,1,1); hold on;
title('Data');
plot(t,y); xlim([0 max(t)]); ylim([-4 4]);
subplot(4,1,2); hold on;
title('Model fit');
plot(t,result,'-k'); xlim([0 max(t)]); ylim([-4 4]);
subplot(4,1,3); hold on;
title('Signal (-1 for trough, +1 for peak)');
plot(t,signal,'r','LineWidth',2); ylim([-1.5 1.5]);
subplot(4,1,4); hold on;
title('Signals marked on data');
markers = abs(signal) > 0;
plot(t,y,'-','Color',[0.1 0.1 0.1]);
scatter(t(markers),result(markers),30,'or','MarkerFaceColor','red');
xlim([0 max(t)]); ylim([-4 4]);

这种方法的主要优点是：

• 您拥有数据的实际模型，因此您可以在信号发生之前预测未来的信号！（例如，修复模型并通过输入未来时间段计算结果）

缺点是您需要选择一个回看窗口，但是您使用的任何用于实时检测的方法都会遇到这个问题。

数据为输入数据，模型拟合为数据拟合正弦波（见代码），信号表示波峰和波谷，数据上标记的信号给人一种算法准确度的印象。注：看模型拟合调整自己的趋势在中间的图表！

这应该让你开始。还有很多关于信号检测理论的优秀书籍（只有谷歌这个词），这些书将深入研究这些类型的技术。祝你好运