问题：

基于Swift的增长时间序列峰值检测

卫财

2023-03-14

谁会有一个好的算法来使用Swift（v3）测量不断增长的时间序列数据的峰值？因此，在数据流入时检测峰值。

例如，平滑z波算法的快速版本。那个算法似乎是合适的。

我需要检测如下所示的峰值。数据包含正数和负数。输出应该是峰值的计数器，和/或该特定样本的真/假。

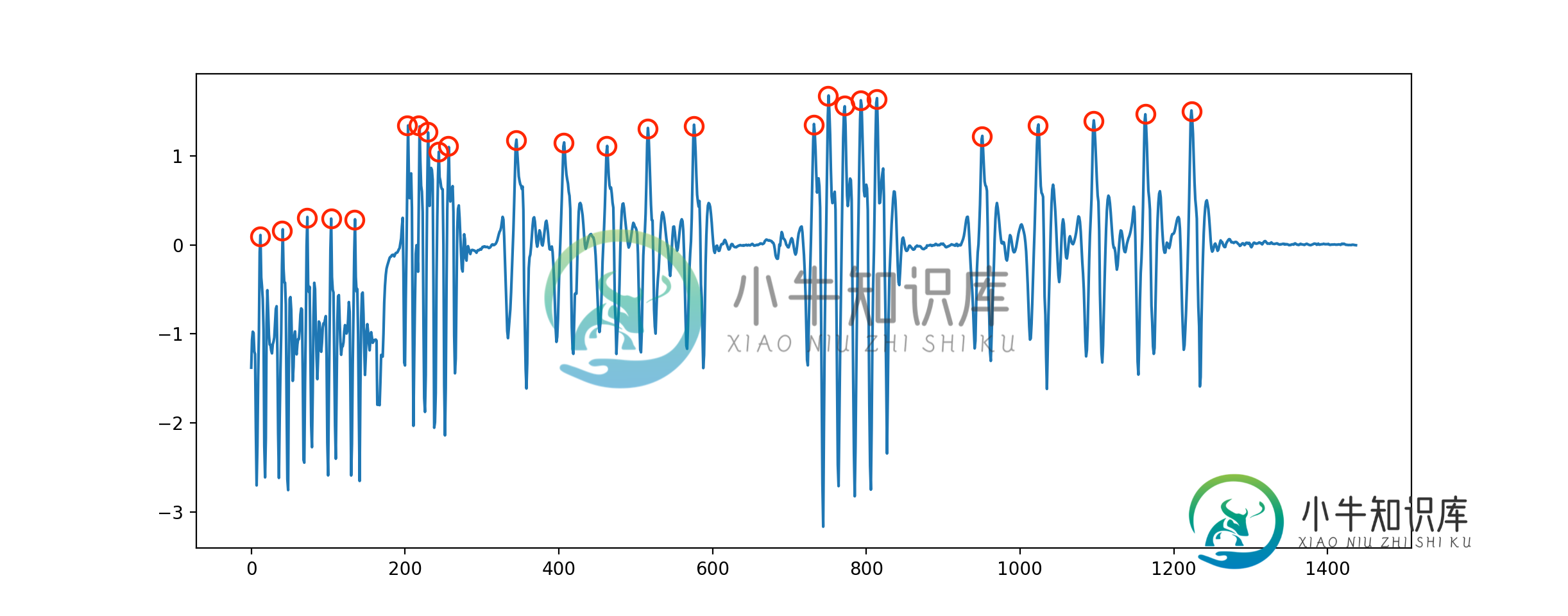
示例数据集（上一系列的摘要）：

let samples = [0.01, -0.02, -0.02, 0.01, -0.01, -0.01, 0.00, 0.10, 0.31,
  -0.10, -0.73, -0.68, 0.21, 1.22, 0.67, -0.59, -1.04, 0.06, 0.42, 0.07, 
  0.03, -0.18, 0.11, -0.06, -0.02, 0.16, 0.21, 0.03, -0.68, -0.89, 0.18, 
  1.31, 0.66, 0.07, -1.62, -0.16, 0.67, 0.19, -0.42, 0.23, -0.05, -0.01,
  0.03, 0.06, 0.27, 0.15, -0.50, -1.18, 0.11, 1.30, 0.93, 0.16, -1.32, 
  -0.10, 0.55, 0.23, -0.03, -0.23, 0.16, -0.04, 0.01, 0.12, 0.35, -0.38,
  -1.11, 0.07, 1.46, 0.61, -0.68, -1.16, 0.29, 0.54, -0.05, 0.02, -0.01,
  0.12, 0.23, 0.29, -0.75, -0.95, 0.11, 1.51, 0.70, -0.30, -1.48, 0.13,
  0.50, 0.18, -0.06, -0.01, -0.02, 0.03, -0.02, 0.06, 0.03, 0.03, 0.02,
  -0.01, 0.01, 0.02, 0.01]

最新消息：感谢Jean Paul首次提供Swift端口。但不确定z-wave算法是否适合此数据集lag=10，threshold=3，influence=0.2对数据集的最后一个系列很好，但是我还没有找到一个适合完整数据集的组合。

问题是：有一个很大的滞后，第一个数据样本不包括在内，我需要每个峰值一个信号，算法需要进一步的工作才能提高效率。

例如，使用Python代码和（例如，lag=5，threshold=2.5，influence=0.7）的完整数据集的结果缺少系列1和系列2的峰值，并且在安静期显示了太多的误报：

完整数据集（应产生25个峰值）：

let samples = [-1.38, -0.97, -1.20, -2.06, -2.26, -0.99, 0.11, -0.47, -0.95, -2.61, -0.88, -0.74, -1.12, -1.19, -1.12, -1.04, -0.72, -1.21, -2.61, -1.41, -0.23, -0.27, -0.43, -1.77, -2.75, -0.61, -0.73, -1.53, -1.02, -1.14, -1.12, -1.06, -0.78, -0.72, -2.41, -1.55, -0.01, -0.44, -0.47, -2.02, -1.66, -0.43, -0.93, -1.51, -0.86, -1.06, -1.10, -0.88, -0.84, -1.26, -2.59, -0.92, 0.29, -0.50, -1.31, -2.40, -0.88, -0.56, -1.09, -1.14, -1.09, -0.90, -0.99, -0.84, -0.75, -2.59, -1.34, -0.08, -0.36, -0.50, -1.89, -1.60, -0.55, -0.78, -1.46, -0.96, -0.97, -1.18, -0.98, -1.10, -1.07, -1.06, -1.79, -1.78, -1.54, -1.25, -1.00, -0.46, -0.27, -0.20, -0.15, -0.13, -0.11, -0.13, -0.09, -0.09, -0.05, 0.02, 0.20, -0.31, -1.35, -0.03, 1.34, 0.52, 0.80, -0.91, -1.26, -0.10, -0.10, 0.53, 0.93, 0.60, -0.83, -1.87, -0.21, 1.26, 0.44, 0.86, 0.73, -2.05, -1.66, 0.31, 1.04, 0.72, 0.63, -0.01, -2.14, -0.48, 0.77, 0.63, 0.58, 0.66, -1.01, -1.28, 0.18, 0.44, 0.09, -0.27, -0.06, 0.06, -0.18, -0.01, -0.08, -0.07, -0.06, -0.06, -0.07, -0.07, -0.06, -0.05, -0.04, -0.03, -0.02, -0.02, -0.03, -0.03, -0.01, 0.01, 0.00, 0.01, 0.05, 0.12, 0.16, 0.25, 0.29, -0.16, -0.69, -1.05, -0.84, -0.54, -0.07, 0.46, 1.12, 1.05, 0.77, 0.68, 0.63, 0.39, -0.96, -1.61, -0.68, -0.14, -0.03, 0.22, 0.31, 0.15, -0.02, 0.11, 0.14, 0.00, 0.04, 0.18, 0.27, 0.14, -0.05, -0.03, -0.08, -0.41, -0.94, -1.03, -0.50, 0.02, 0.52, 1.10, 1.03, 0.79, 0.69, 0.55, -0.34, -1.17, -0.89, -0.54, -0.22, 0.37, 0.47, 0.39, 0.23, 0.00, -0.02, 0.05, 0.10, 0.12, 0.09, 0.05, -0.12, -0.50, -0.89, -0.89, -0.48, 0.00, 0.43, 1.03, 0.95, 0.67, 0.64, 0.47, -0.07, -0.85, -1.02, -0.73, -0.08, 0.38, 0.46, 0.32, 0.15, 0.01, -0.01, 0.09, 0.20, 0.23, 0.19, 0.12, -0.50, -1.17, -0.97, -0.12, 0.15, 0.70, 1.31, 0.97, 0.45, 0.27, -0.73, -1.00, -0.52, -0.27, 0.10, 0.33, 0.34, 0.23, 0.07, -0.04, -0.27, -0.24, 0.10, 0.21, 0.05, -0.07, 0.04, 0.21, 0.29, 0.16, -0.45, -1.13, -0.93, -0.28, 0.04, 0.72, 1.35, 1.05, 0.56, 0.43, 0.17, -0.59, -1.38, -0.76, 0.10, 0.44, 0.46, 0.35, 0.12, -0.07, -0.05, -0.01, -0.07, -0.04, 0.01, 0.01, 0.06, 0.02, -0.03, -0.05, 0.00, 0.01, -0.02, -0.03, -0.02, -0.01, 0.00, -0.01, 0.00, -0.01, 0.00, -0.01, -0.01, 0.00, 0.01, -0.01, -0.01, 0.00, 0.00, 0.01, 0.01, 0.01, 0.04, 0.06, 0.05, 0.05, 0.04, 0.03, 0.00, -0.12, -0.16, -0.09, -0.01, 0.14, 0.07, 0.06, 0.00, -0.03, 0.00, 0.06, 0.06, -0.04, -0.11, -0.02, 0.13, 0.18, 0.21, 0.01, -0.31, -0.92, -1.35, -0.62, 0.03, 0.78, 1.36, 1.07, 0.59, 0.75, 0.42, -1.65, -3.16, -0.97, 0.24, 1.44, 1.50, 0.84, 0.47, 0.56, 0.40, -1.50, -2.71, -1.22, 0.01, 1.20, 1.55, 0.92, 0.44, 0.66, 0.73, -0.43, -2.34, -2.28, -0.72, 0.36, 1.41, 1.56, 0.89, 0.54, 0.67, 0.39, -1.78, -2.75, -1.07, -0.07, 1.16, 1.65, 0.80, 0.47, 0.73, 0.86, -0.24, -1.52, -1.68, -0.39, 0.02, 0.38, 0.60, 0.49, 0.02, -0.42, -0.31, -0.01, 0.08, 0.00, -0.07, -0.05, -0.01, -0.02, -0.04, -0.05, -0.02, -0.01, -0.02, -0.02, -0.03, -0.05, -0.04, -0.03, -0.01, -0.01, 0.00, -0.01, 0.00, 0.01, 0.00, 0.00, 0.00, 0.01, 0.01, -0.01, -0.03, -0.02, -0.01, 0.00, 0.00, 0.00, -0.01, 0.01, 0.00, -0.01, 0.02, 0.07, 0.15, 0.28, 0.31, 0.08, -0.26, -0.54, -0.96, -1.08, -0.27, 0.01, 0.45, 1.18, 1.07, 0.71, 0.65, 0.20, -0.80, -1.30, -0.74, -0.24, 0.29, 0.47, 0.34, 0.15, 0.02, 0.03, -0.02, -0.16, -0.13, 0.05, 0.09, -0.01, -0.08, -0.06, 0.03, 0.13, 0.19, 0.23, 0.18, 0.10, -0.07, -0.44, -0.91, -1.05, -0.64, -0.08, 0.50, 1.12, 1.35, 0.89, 0.58, 0.54, -0.58, -1.27, -1.20, -0.48, 0.19, 0.62, 0.62, 0.37, -0.01, -0.35, -0.33, 0.07, 0.29, 0.10, -0.14, -0.10, 0.07, 0.07, 0.01, 0.03, 0.09, 0.20, 0.32, 0.26, -0.02, -0.32, -0.78, -1.25, -0.93, -0.16, 0.30, 0.88, 1.40, 1.14, 0.72, 0.48, -0.54, -1.21, -1.13, -0.41, 0.18, 0.51, 0.53, 0.36, 0.11, -0.03, -0.09, -0.28, -0.11, 0.11, 0.15, 0.04, -0.08, -0.04, 0.04, 0.09, 0.16, 0.26, 0.43, 0.09, -0.88, -1.46, -0.64, -0.16, 0.43, 1.37, 1.34, 0.84, 0.52, -0.17, -0.87, -1.22, -0.76, 0.03, 0.47, 0.60, 0.36, 0.04, -0.09, -0.03, 0.02, -0.04, 0.04, 0.12, 0.13, 0.19, 0.27, 0.31, 0.18, -0.42, -0.99, -1.13, -0.75, -0.22, 0.50, 1.42, 1.41, 0.98, 0.51, 0.29, -0.69, -1.59, -0.88, -0.13, 0.31, 0.49, 0.46, 0.30, 0.05, -0.08, -0.03, 0.01, -0.04, -0.06, 0.02, 0.03, 0.01, -0.02, 0.01, 0.04, 0.06, 0.04, 0.03, 0.02, 0.03, 0.03, 0.01, -0.01, 0.00, 0.02, 0.00, 0.02, 0.02, 0.02, -0.02, -0.01, 0.02, 0.02, 0.01, 0.02, 0.02, 0.02, 0.02, 0.04, 0.03, 0.01, 0.01, 0.02, 0.01, 0.01, 0.01, 0.02, 0.01, 0.00, 0.01, 0.01, 0.00, 0.00, 0.01, 0.00, 0.00, 0.01, 0.00, 0.02, 0.00, 0.00, 0.01, 0.01, 0.00, 0.00, 0.01, 0.01, 0.00, 0.00, 0.00, 0.01, 0.01, 0.00, 0.01, 0.00, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.01, 0.01, 0.01, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00]

因此，我不确定z-wave算法是否适合这种数据集。

共有1个答案

阎阎宝

2023-03-14

好的，为了快速帮助你们：这里是一个将algo翻译成Swift的翻译：Swift沙盒中的演示

警告：我绝不是一个敏捷的程序员，所以可能会有错误！

还要注意，我已经关闭了负面信号，因为OP的目的我们只想要正面信号。

银行代码：

import Glibc // or Darwin/ Foundation/ Cocoa/ UIKit (depending on OS)

// Function to calculate the arithmetic mean
func arithmeticMean(array: [Double]) -> Double {
    var total: Double = 0
    for number in array {
        total += number
    }
    return total / Double(array.count)
}

// Function to calculate the standard deviation
func standardDeviation(array: [Double]) -> Double
{
    let length = Double(array.count)
    let avg = array.reduce(0, {$0 + $1}) / length
    let sumOfSquaredAvgDiff = array.map { pow($0 - avg, 2.0)}.reduce(0, {$0 + $1})
    return sqrt(sumOfSquaredAvgDiff / length)
}

// Function to extract some range from an array
func subArray<T>(array: [T], s: Int, e: Int) -> [T] {
    if e > array.count {
        return []
    }
    return Array(array[s..<min(e, array.count)])
}

// Smooth z-score thresholding filter
func ThresholdingAlgo(y: [Double],lag: Int,threshold: Double,influence: Double) -> ([Int],[Double],[Double]) {

    // Create arrays
    var signals   = Array(repeating: 0, count: y.count)
    var filteredY = Array(repeating: 0.0, count: y.count)
    var avgFilter = Array(repeating: 0.0, count: y.count)
    var stdFilter = Array(repeating: 0.0, count: y.count)

    // Initialise variables
    for i in 0...lag-1 {
        signals[i] = 0
        filteredY[i] = y[i]
    }

    // Start filter
    avgFilter[lag-1] = arithmeticMean(array: subArray(array: y, s: 0, e: lag-1))
    stdFilter[lag-1] = standardDeviation(array: subArray(array: y, s: 0, e: lag-1))

    for i in lag...y.count-1 {
        if abs(y[i] - avgFilter[i-1]) > threshold*stdFilter[i-1] {
            if y[i] > avgFilter[i-1] {
                signals[i] = 1      // Positive signal
            } else {
                // Negative signals are turned off for this application
                //signals[i] = -1       // Negative signal
            }
            filteredY[i] = influence*y[i] + (1-influence)*filteredY[i-1]
        } else {
            signals[i] = 0          // No signal
            filteredY[i] = y[i]
        }
        // Adjust the filters
        avgFilter[i] = arithmeticMean(array: subArray(array: filteredY, s: i-lag, e: i))
        stdFilter[i] = standardDeviation(array: subArray(array: filteredY, s: i-lag, e: i))
    }

    return (signals,avgFilter,stdFilter)
}

// Demo
let samples = [0.01, -0.02, -0.02, 0.01, -0.01, -0.01, 0.00, 0.10, 0.31,
  -0.10, -0.73, -0.68, 0.21, 1.22, 0.67, -0.59, -1.04, 0.06, 0.42, 0.07, 
  0.03, -0.18, 0.11, -0.06, -0.02, 0.16, 0.21, 0.03, -0.68, -0.89, 0.18, 
  1.31, 0.66, 0.07, -1.62, -0.16, 0.67, 0.19, -0.42, 0.23, -0.05, -0.01,
  0.03, 0.06, 0.27, 0.15, -0.50, -1.18, 0.11, 1.30, 0.93, 0.16, -1.32, 
  -0.10, 0.55, 0.23, -0.03, -0.23, 0.16, -0.04, 0.01, 0.12, 0.35, -0.38,
  -1.11, 0.07, 1.46, 0.61, -0.68, -1.16, 0.29, 0.54, -0.05, 0.02, -0.01,
  0.12, 0.23, 0.29, -0.75, -0.95, 0.11, 1.51, 0.70, -0.30, -1.48, 0.13,
  0.50, 0.18, -0.06, -0.01, -0.02, 0.03, -0.02, 0.06, 0.03, 0.03, 0.02,
  -0.01, 0.01, 0.02, 0.01]

// Run filter
let (signals,avgFilter,stdFilter) = ThresholdingAlgo(y: samples, lag: 10, threshold: 3, influence: 0.2)
// Print output to console
print("\nOutput: \n ")
for i in 0...signals.count - 1 {
    print("Data point \(i)\t\t sample: \(samples[i]) \t signal: \(signals[i])\n")
}

// Raw data for creating a plot in Excel
print("\n \n Raw data for creating a plot in Excel: \n ")
for i in 0...signals.count - 1 {
    print("\(i+1)\t\(samples[i])\t\(signals[i])\t\(avgFilter[i])\t\(stdFilter[i])\n")
}

对于样例数据的结果（对于延迟=10，阈值=3，影响=0.2）：

通过对均值和标准偏差的滞后使用不同的值，可以提高算法的性能。例如。：

// Smooth z-score thresholding filter
func ThresholdingAlgo(y: [Double], lagMean: Int, lagStd: Int, threshold: Double, influenceMean: Double, influenceStd: Double) -> ([Int],[Double],[Double]) {

    // Create arrays
    var signals   = Array(repeating: 0, count: y.count)
    var filteredYmean = Array(repeating: 0.0, count: y.count)
    var filteredYstd = Array(repeating: 0.0, count: y.count)
    var avgFilter = Array(repeating: 0.0, count: y.count)
    var stdFilter = Array(repeating: 0.0, count: y.count)

    // Initialise variables
    for i in 0...lagMean-1 {
        signals[i] = 0
        filteredYmean[i] = y[i]
        filteredYstd[i] = y[i]
    }

    // Start filter
    avgFilter[lagMean-1] = arithmeticMean(array: subArray(array: y, s: 0, e: lagMean-1))
    stdFilter[lagStd-1] = standardDeviation(array: subArray(array: y, s: 0, e: lagStd-1))

    for i in max(lagMean,lagStd)...y.count-1 {
        if abs(y[i] - avgFilter[i-1]) > threshold*stdFilter[i-1] {
            if y[i] > avgFilter[i-1] {
                signals[i] = 1      // Positive signal
            } else {
                signals[i] = -1       // Negative signal
            }
            filteredYmean[i] = influenceMean*y[i] + (1-influenceMean)*filteredYmean[i-1]
            filteredYstd[i] = influenceStd*y[i] + (1-influenceStd)*filteredYstd[i-1]
        } else {
            signals[i] = 0          // No signal
            filteredYmean[i] = y[i]
            filteredYstd[i] = y[i]
        }
        // Adjust the filters
        avgFilter[i] = arithmeticMean(array: subArray(array: filteredYmean, s: i-lagMean, e: i))
        stdFilter[i] = standardDeviation(array: subArray(array: filteredYstd, s: i-lagStd, e: i))
    }

    return (signals,avgFilter,stdFilter)
}

然后使用例如let（signals，avgFilter，stdFilter）=阈值algo（y:samples，lagMean:10，lagStd:100，threshold:2，influenceMean:0.5，influenceStd:0.1）可以得到更好的结果：

类似资料：

不均匀间隔时间序列中的峰值检测

我正在使用一个数据集，其中包含与相结合的度量值，例如：我试图检测和删除可能出现的潜在峰值，如度量值。到目前为止，我发现了一些东西： > 这个数据集的时间间隔从15秒一直到25分钟，这使得它非常不均匀峰的宽度无法事先确定峰值高度与其他值明显偏离时间步长的标准化只应在去除异常值后进行，因为它们会干扰结果由于其他异常（例如，负值、平线），即使没有这些异常，也“不可能”使其变得均匀，因为峰值会
噪声正弦时间序列中的实时峰值检测

我一直试图实时检测正弦时间序列数据中的峰值，但迄今为止没有成功。我似乎找不到一种能够以合理的精度检测正弦信号峰值的实时算法。我要么没有检测到峰值，要么正弦波上有无数个点被检测为峰值。对于类似正弦波且可能包含一些随机噪声的输入信号，什么是好的实时算法？作为一个简单的测试案例，考虑一个稳定的正弦波，它总是相同的频率和振幅。（确切的频率和振幅并不重要；我任意选择了60赫兹的频率，振幅为/− 使用Je
时间序列信号峰值聚类检测算法

我有一个带有开/关数据的二进制时间序列数据集。on通常是短暂的，因此看起来像一个峰值。这就是它的样子。我已经检测到了峰值，并提取了峰值之间的时间间隔，并且也有数据（底部的红色小双向箭头）。问题是，可以看出，峰值是聚集的，我想对突发大小（集群中的峰值数量）、突发间隔（第一个集群的最后一个峰值和最后一个集群的第一个峰值之间的距离）、突发数量等进行量化。一旦确定了集群，所有这些都很容易做到。这可以通
实时时序数据中的峰值信号检测

更新：到目前为止，性能最好的算法就是这个。这个问题探索了检测实时时间序列数据中突然峰值的鲁棒算法。考虑下面的示例数据：此数据的示例为Matlab格式（但此问题与语言无关，而与算法有关）：你可以清楚地看到有三个大峰和一些小峰。此数据集是问题所涉及的timeseries数据集类的一个特定示例。此类数据集具有两个一般特征：存在具有一般平均值的基本噪声存在明显偏离噪声的大“峰值”或“更高数据点
Python-二维阵列中的峰值检测

问题内容：我正在帮助兽医诊所测量狗爪下的压力。我使用Python进行数据分析，现在我被困在试图将爪子分成（解剖）子区域。我制作了每个爪子的2D数组，其中包含爪子随时间推移已加载的每个传感器的最大值。这是一个爪子的示例，我使用Excel绘制了要“检测”的区域。这些是传感器周围具有最大最大值的2 x 2框，它们的总和最大。因此，我尝试了一些实验，并决定只寻找每一列和每一行的最大值（由于爪子的形状
基于（？）LSTM的多变量时间序列分类

我对时间序列分类比较陌生，正在寻求帮助：我有一个包含5000个多元时间序列的数据集，每个数据集由21个变量组成，时间周期为3年，类别信息为1或0。我想做的是对一个新的输入进行分类，它在3年的时间内由21个变量组成。就目前而言，经过几天的研究，我还没有找到（或显然没有理解）将多变量时间序列输入LSTM的方法。有没有可能的解决办法？我目前的想法是将5000个时间序列“合并”成一个，并向每个序列添

基于Swift的增长时间序列峰值检测

共有1个答案

相关问答

相关文章

相关阅读

相关工具

相关文档