附录5

设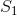是 g 系集的任意可测子集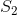，是 f 系集的一个子集，对其执行运算T之后，可以得出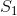。于是：

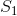
设是一个运算符，对将一个集合中的所有函数都平移时间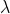。由于T是时不变的，从而可以与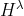交换，于是，

因此，如果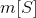是集合S的概率度量，则：

其中第二个等式是根据 g 空间中度量的定义得出，第三个是因为 f 系集是平稳的，最后一个是根据 g 度量的定义得出。

为了证明在时不变运算下，各态历经性质得以保持，设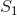是g系集的一个子集，对其进行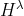运算时是时不变的，设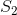是由所有将会变换为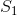的函数 f 组成的集合。于是，

使得对于所有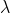，都包含在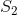中。现在，由于：

这意味着，对于所有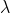且：

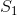这一矛盾表明，不存在。