附录4：给定约束条件下信息生成速率的最大化

假定我们对符号序列有一组约束条件，这些符号为有限状态类型，因此，可以用线性图进行表示。设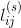是在由状态i过渡到状态j时，可能出现的各个符号的长度。设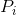是不同状态的频率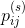，是在状态i下选择符号s，并转换为状态j的的概率，在这些约束条件下，如何选择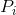和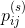的分布，使生成信息的速率达到最大？这些约束条件限定了一个离散信道，最大生成速率必须小于或等于这个信道的容量C，这是因为，如果所有大长度的序列块都是等概率的，就会得到这一结果，如果可能的话，它就是最好的。我们将会证明，通过正确地选择频率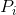和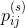，就能实现这一速率。

所考虑的速率是：

。

设。显然，对于一个最大值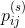，。对最大值的约束条件是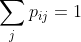，，。因此，我们使下式达到最大：

。

解出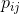

。

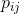由于：

，

。

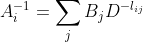
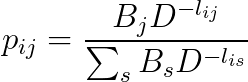D的正确值为容量C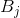，是下式的解：

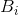
因为：

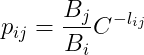
或者：

。

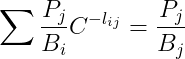因此，如果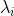满足

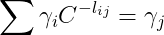
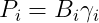
由于C满足：

，

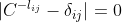所以关于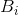和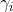的方程组都成立。

在这种情况下，该速率为：

但是：

因此，该速率为C，而且它从来不会被超越，所以它就是最大值，从而表明上面所取解的合理性。