11. 有噪声离散信道的表示

我们现在考虑信号在传输过程中或者在某终端处受到噪声干扰的情景。这意味着，接收信号不一定与发送器发出的信号相同。可以区分两种情景。如果一个特定的传送信号总是生成相同的接收信号，即接收信号是传送信号的确定函数，可以将这种影响称为“失真”。如果这一函数有逆函数——任何两个传送信号都不会生成相同的接收信号，只需要对接收信号执行逆函数运算，就可以校正该失真，至少在原理上如此。

这里关心的情景是：在传输过程中，信号变化并非总是一致的。在这种情况下，我们可以假定接收信号E是传送信号S及一个第二变量的函数，这个第二变量就是噪声N。

和前面的消息一样，可以认为噪声是一个随机变量。一般情况下，它可以用一个适当的随机过程来表示。我们将要考虑的最一般有噪声离散信道类型是前面介绍的有限状态无噪声信道的一种推广。我们假定状态数目有限，概率集合为：

。

这一概率是指，如果信道处于状态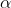并传送符号i，则接收到符号j，且信道变为状态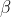的概率。因此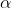，和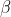的取值范围为所有可能状态，i的取值范围为所有可能发送的信号，j的取值范围是所有可能接收的信号。当连续信号受到噪声的干扰相互独立时，只有一种状态，可以用一组转换概率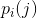来描述，也就是将发送信号i接收为j的概率。

如果一个有噪声信道从一个信源那里接收内容，则有两个统计进程在发挥作用：信源和噪声。因此，可以计算许多种熵。首先，存在一个信源的熵H(x)，或者是信道输入的熵（如果发送器是非奇异的，则这两个熵相等）。信道输出（也就是接收信号）的熵用H(y)表示。在无噪声情况下，H(y)=H(x)。输入与输出的联合熵为H(xy)。最后，有两个条件熵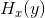和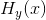，分别是在输入已知时输出的熵和输出已知时输入的熵。在这些量中，存在如下关系：

。

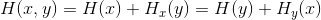所有这些熵都可以基于“每秒”或“每符号”来计算。