23. 两个系集之和的熵

如果有两个函数系集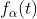和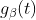，可以通过“加法”构成一个新系集。假定第一个系集的概率密度函数，第二个的为。因此，两者之和的概率密度由以下卷积给出：

。

在物理上，这种情况对应于将由原函数系集表示的噪声或信号求和。

在附录6中推导了以下结果。

定理15：设两个系集的平均功率为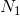和，并设其熵功率为和。则两者之和的熵的上下限为：

。

高斯白噪声有一种特殊的性质：如果在特定意义下，信号功率相对于噪声很低，则它可以吸收任何向其增加的噪声或信号系集，所得到的熵功率近似等于 白噪声功率和信号功率之和（从平均信号值的角度来测量，信号功率通常为0）。

考虑与这些系集相关联的函数空间，它有n个维度。白噪声与这个空间中的球形高斯分布相对应。信号系集对应于另一种概率分布，不一定是高斯分布或球形分布。设这一分布关于其重心的二阶矩为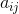。因此，如果为密度分布函数，则：

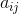
其中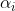：是重心的坐标。现在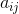是正定二次型，我们可以旋转坐标系，使它对准这一形式的主要方向。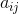于是化简为对角形式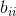。我们要求每个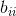相对于N都很小（N为该球形分布半径的平方）。

在这种情况下，噪声与信号的卷积近似生成一个高斯分布，其对应的二次型为：

。

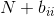这一分布的熵功率为：

或近似为：

最后一项为信号功率，第一项为噪声功率。