29. 信息产生速率的计算

信息产生速率的定义在许多方面都类似于信道容量的定义。在信息产生速率的定义中，

其中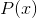和为固定值。而在信道容量的定义中，

其中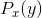固定，可能还有一个或多个形式的其他约束条件（例如，平均功率限制）。

对于确定信源信息产生速率的一般性最大化问题，可以给出部分解。利用拉格朗日方法，考虑：

当对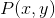取一次变分时，由变分方程可以得出：

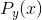
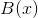其中，通过确定给出所需要的保真度，通过选择以满足：

这表明，在采用最佳编码方式时，对于接收到的各个y，其发送消息的条件概率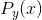将随着x与y之间的距离函数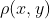指数下降。

在某些特殊情况下，距离函数仅取决于x与y之间的（向量）差，

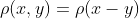
在此情况下，有：

因此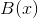，为常数，比如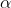，且

遗憾的是，这些正式解在特定情况下很难计算，似乎没有多少价值。事实上，仅在有限几种非常简单的情况下，才能实际计算出信息产生速率。

如果距离函数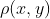是x与y之间的均方差，且消息系集为白噪声，则可以确定该速率。在这种情况下，有：

其中，。但当为白噪声时，得到，它等于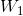，其中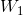是消息系集的带宽。因此，

其中Q是平均消息功率。它证明了以下定理：

定理22：在采用保真度的RMS度量时，一个功率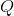为、带宽为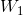的白噪声信源，其信息产生速率为：

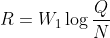
其中，N是允许原消息与接收消息之间出现的均方误差。

更一般地，对于任意信源，我们可以针对均方误差准则，给出该速率的上下限不等式。

定理23：对于带宽为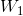的任意信源，其信息产生速率的上下限为：

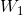
其中Q是信源的平均功率，是熵功率，N是允许的均方误差。

在给定时，在白噪声情况下得到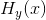的最大值，由此推出不等式中的下限。如果我们不是采用最佳方式来放置在证明定理21时使用的各个点，而是将它们随机放在半径为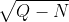的球体中，则可以得出上限。

致谢

本文作者衷心地感谢实验室的各位同事，特别是H. W. Bode博士、J. R. Pierce博士、B. McMillan博士和B. M. Oliver博士，他们在此论文的撰写期间提出了许多富有裨益的建议和批评。还要感谢维纳教授，他对平稳系集的滤波与预测问题的精彩解法深刻地影响了本文作者在这一领域的思想。