附录6

上限可由以下事实推导得出：当功率为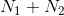时，白噪声的熵最大。在这种情况下，熵功率为。

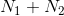为了得到下限，假定有两个n维分布和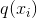，其熵功率分别为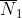和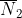。p和q的卷积为：

，

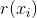为了使该卷积的熵功率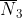最小，p和q应当取什么形式？

r 的熵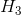由下式给出：

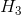
我们希望在以下约束条件下，使上式的取值最小：

于是，我们考虑：

若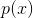在一个特定的参数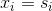处变化，则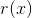中的变化为：

且：

q 变化时的情况与此类似。因此，取最小值的条件为：

如果将第一个等式乘以，第二个等式乘以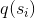，并对积分，则得到：

或者，对和求解，并代入方程，

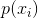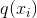现在假定和是正态的

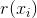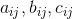则将具有正态二次型。如果这些形式的逆为，则：

我们希望证明，当且仅当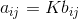时，这些函数满足最小化条件，因此，在这些约束条件下给出最小值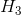。首先，有：

它应当等于：

这要求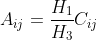。在这种情况下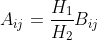，，两个等式简化为恒等式。