9. 无噪声信道的基本定理

我们现在将证明H确定了在最高效编码方式下所需要的信道容量，从而表明我们将H解读为信息的生成速率是合理的。

定理9：设一个信源的熵为H（比特/符号），一个信道的容量为C（比特/秒）。有可能采用某种方式对该信源的输出进行编码，从而可以在该信道上以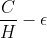符号/秒的平均速率上进行传送，其中为任意小。不可能以大于的平均速率进行传送。

反过来表述这一定理就是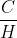：不可能被超越。它可以这样证明：由于传送器必然是非奇异的，所以每秒钟输入给信道的内容的熵等于信源的熵，而这个熵不可能超过信道容量。因此，，每秒的符号数。

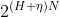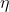定理的第一部分可以用两种不同方式证明。第一种方法是考虑信源生成的所有N符号序列的集合。当N很大时，我们可以将这些序列分为两组，一组内的成员数小于，第二组的成员数小于（其中R是不同符号数的对数），而且其总概率小于。随着N的增大，和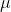趋近于0。信道中持续时间为T的信号数大于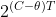，当T很大时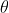，很小。如果我们选择：

则当N和T足够大时（无论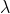多么小）时，总有足够多的信道符号序列可供高概率组使用，而且还会有一些富余。可以采用任意一对一方式将高概率组编码到这个集合中。剩下的序列用较长的序列表示，这些较长序列的开头和结尾是一个未为高概率组使用的序列。这一特殊序列充当着不同代码的起始与结束标志。只要有足够的时间，就可以为所有低概率消息提供足够的不同序列。这就要求：

其中，很小。由此得出，平均传送速率（单位：消息符号/秒）将大于：

。

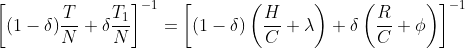随着N的增大，趋近于0，该速率趋近于。

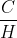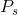另一种执行这一编码过程并证明该定理的方法可以描述如下：按概率的递减顺序排列长度为N的消息，并假定它们的概率为。令；即，是一直到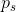（但不包含）的累积概率。我们首先将其编码为二进制。将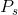扩展为一个二进制数，即可得到消息s的二进制编码。这一扩展一直执行到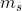位，其中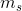是满足下式的整数：

因此，高概率消息用短代码表示，低概率消息用长代码表示。由这些不等式可以得到：

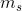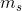的代码与它前面的所有代码相比，在位中的一个或多个位置有所不同。由于所有其余都至少要大出，因此，它们的二进制扩展会在前位中有所不同。因此，所有这些编码都是不同的，从而有可能从消息的编码中恢复出消息。如果信道序列还不是二进制数位序列，则可以采用任意一种方式将它们表示为二进制数，然后再将二进制编码转换为适于信道传送的信号。

原消息中每个符号所使用的平均二进制数位数H'很容易估计出来。有：

。

但是，

因此，

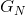
随着N的增大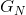，趋近于H，即信源的熵，H'也趋近于H。

由此可以看出，当仅使用N个符号的有限延迟时，编码中的低效性不一定大于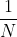加上H与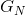之差，其中H为真实熵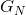，是为长度为N的序列计算所得的熵。因此，所需时间超出理想值的百分比小于：

。

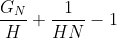这一方法基本上与R. M. Fano独立发现的方法相同。他的方法是将长度为N的消息按照概率的降序排列。尽可能将这一系列消息划分为两个概率接近相等的组。如果消息属于第一组，则它的第1个二进制数位为0，否则为1。然后再采用类似方式，进一步将这些组分为概率近似相等的子集，具体的子集决定了第2个二进制数位。继续这一过程，直到每个子集中仅包含一条消息为止。容易看出，除了微小的差别之外（通常是在最后一位），这一方法与上述算术过程基本相同。