24. 连续信道的容量
在连续信道中,输入信号或所传送的信号是某一特定集合中的连续时间函数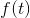 ,输出信号或所接收的信号是前述信号受到干扰后的结果。我们仅考虑传送信号和接收信号的带宽都不超过W的情况。因此,对于某一时间T,可以用
,输出信号或所接收的信号是前述信号受到干扰后的结果。我们仅考虑传送信号和接收信号的带宽都不超过W的情况。因此,对于某一时间T,可以用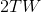 个数字来指定这些信号,用有限维分布函数来指明其统计结构。因此,传送信号的统计信息由下式给出:
个数字来指定这些信号,用有限维分布函数来指明其统计结构。因此,传送信号的统计信息由下式给出:
噪声的统计信息由下面的条件概率分布给出:
。
可以采用一种类似于离散信道的方式来定义连续信道的信息传送速率,即:

式中,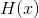 是输入的熵,
是输入的熵, 是疑义度。信道容量C定义为:在所有可能选择的系集范围内改变输入,R取得的最大值。这意味着,采用一种有限维近似,我们必须改变
是疑义度。信道容量C定义为:在所有可能选择的系集范围内改变输入,R取得的最大值。这意味着,采用一种有限维近似,我们必须改变 ,使下式取最大值:
,使下式取最大值:
。
事实上,,由此可将上式记为:
。
因此,信道容量可表示如下:
由这一形式容易看出,R和C与坐标系无关,因为,当x和y以任意一对一方式进行变换时,中的分子和分母将乘以相同因子。C的这一积分表达式要比
更具一般性。只要正确解读,这一表述式的结果总是存在的,而在某些情况下,
可能会取未定式
 。例如,在其n维近似中,如果x局限于一个维度小于n的表面,就会出现上述情况。
。例如,在其n维近似中,如果x局限于一个维度小于n的表面,就会出现上述情况。
如果在计算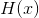 和
和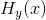 时的对数底数为2,则和离散情况中一样,C表示每秒钟以任意小的疑义度通过该信道传送的最大二进制数位个数。从物理上来说,将信道空间划分为足够多的小单元格,使得在一个单元格内,信号x受干扰后变到点y的概率密度
时的对数底数为2,则和离散情况中一样,C表示每秒钟以任意小的疑义度通过该信道传送的最大二进制数位个数。从物理上来说,将信道空间划分为足够多的小单元格,使得在一个单元格内,信号x受干扰后变到点y的概率密度 基本为恒定。如果将这些单元格看作不同点,则此情况下离散信道中基本相同,当时的证明过程在这里同样适用。但从物理上容易看出,在任意实际情况下,只要这些区域足够小,这种将体积量化为独立点的过程不会显著改变最终的答案。因此,这一容量就是离散细分区域的容量的极限,也就是上述定义的连续容量。
基本为恒定。如果将这些单元格看作不同点,则此情况下离散信道中基本相同,当时的证明过程在这里同样适用。但从物理上容易看出,在任意实际情况下,只要这些区域足够小,这种将体积量化为独立点的过程不会显著改变最终的答案。因此,这一容量就是离散细分区域的容量的极限,也就是上述定义的连续容量。
在数学上,可以首先证明(见附录7):如果u为消息,x是信号,y是接收信号(受到了噪声的干扰),v是恢复得出的消息,则有:无论对u执行什么操作以得到x,或者对y执行什么操作以得到v,都可以得到
因此,无论如何对二进制数位进行编码,以得到信号,也无论如何对接收信号进行解码以恢复出消息,二进制数位的离散速率都不会超出前面定义的信道容量。另一方面,在非常一般的情况下,有可能找出一种编码系统,以所期望的小疑义度或错误频率,以速率C传送二进制数位。例如,如果为信道函数取一个有限维近似空间,除了一些概率为零的点集之外, 在x和y上都是连续的,则上述结果成立。
在x和y上都是连续的,则上述结果成立。
在向信号添加一个与信号独立的噪声时(在概率意义上独立),会出现一种重要的特例。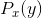 只是差值
只是差值 的函数,
的函数,
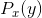
我们可以为噪声指定一个确定的熵(与信号的统计信息相独立),即分布 的熵。这个熵用
的熵。这个熵用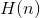 表示。
表示。
定理16:如果信号与噪声独立,且接收信号是传送信号与噪声的和,则传送速率为:
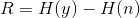
即接收信号的熵减去噪声的熵。信道容量为:
由于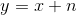 ,所以有:
,所以有:

展开左侧,并利用x与n相独立这一事实,有:
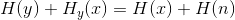 。
。
因此,
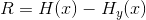 。
。
由于 与
与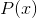 独立,要使取最大值,则需要使
独立,要使取最大值,则需要使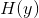 (接收信号的熵)取最大值。如果对传送信号的系集具有特定的约束条件,则必然在遵守这些约束条件的情况下,使接收信号的熵最大化。
(接收信号的熵)取最大值。如果对传送信号的系集具有特定的约束条件,则必然在遵守这些约束条件的情况下,使接收信号的熵最大化。

