细解卷积神经网络

卷积运算

再次引用上一篇里的内容《自己动手做聊天机器人 二十二-神奇算法之人工神经网络》：

卷积英文是convolution(英文含义是：盘绕、弯曲、错综复杂)，数学表达是：

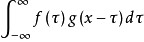
上面连续的情形如果不好理解，可以转成离散的来理解，其实就相当于两个多项式相乘，如：(x*x+3*x+2)(2*x+5)，计算他的方法是两个多项式的系数分别交叉相乘，最后相加。用一句话概括就是：多项式相乘，相当于系数向量的卷积。

如果再不好理解，我们可以通俗点来讲：卷积就相当于在一定范围内做平移并求平均值。比如说回声可以理解为原始声音的卷积结果，因为回声是原始声音经过很多物体反射回来声音揉在一起。再比如说回声可以理解为把信号分解成无穷多的冲击信号，然后再进行冲击响应的叠加。再比如说把一张图像做卷积运算，并把计算结果替换原来的像素点，可以实现一种特殊的模糊，这种模糊其实是一种新的特征提取，提取的特征就是图像的纹路。总之卷积就是先打乱，再叠加。

下面我们在看上面的积分公式，需要注意的是这里是对τ积分，不是对x积分。也就是说对于固定的x，找到x附近的所有变量，求两个函数的乘积，并求和。

卷积神经网络

英文简称CNN，大家并不陌生，因为你可能见过DNN(深度神经网络)、RNN(循环神经网络)。CNN主要应用领域是图像处理，它本质上是一个分类器。

卷积神经网络为什么这么深得人心呢？因为在卷积神经网络的第一层就是特征提取层，也就是不需要我们自己做特征提取的工作，而是直接把原始图像作为输入，这带来了很大的便利，归根结底还是归功于卷积运算的神奇。

那么第一层是怎么利用卷积运算做特征提取的呢？我们还是通过图像处理的例子来说明。参考生物学的视觉结构，当人眼观察一个事物的时候，并不是每个视神经细胞感知所有看到的“像素”，而是一个神经细胞负责一小块视野，也就是说假设看到的全部视野是1000像素，而神经细胞有10个，那么一个神经细胞就负责比1000/10得到的平均值大一圈的范围，也就是200像素，一个细胞负责200个像素，10个细胞一共是2000个像素，大于1000个像素，说明有重叠。这和上面卷积运算的原理很像。用一张图来表示如下：

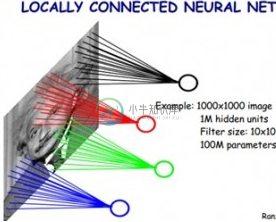
什么是卷积核

先看下面这张图，这是计算5*5矩阵中间的3*3部分的卷积值

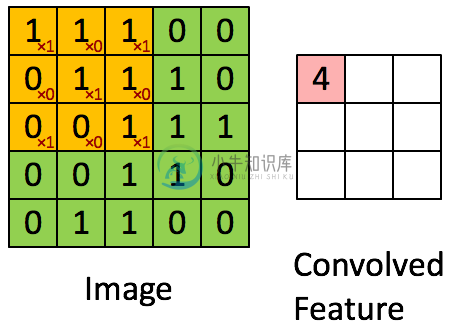
绿色部分是一个5*5的矩阵，标橙的部分说明正在进行卷积计算，×1表示算上这个单元的值，×0表示不计算，这样得出的结果1×1+1×0+1×1+0×0+1×1+1×0+0×1+0×0+1×1=4，这样计算出了第一个元素的卷积

我们继续让这个橙色部分移动并计算，最终会得到如下结果：

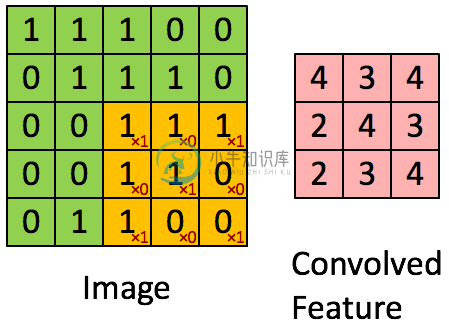
那么这里的橙色(标记×1或×0)的矩阵(一般都是奇数行奇数列)就叫做卷积核，即

1 0 1
0 1 0
1 0 1

卷积计算实际上是一种对图像元素的矩阵变换，是提取图像特征的方法，多种卷积核可以提取多种特征。每一种卷积核生成的图像都叫做一个通道，这回也就理解了photoshop中“通道”的概念了吧

一个卷积核覆盖的原始图像的范围(上面就是5*5矩阵范围)叫做感受野(receptive field)，这个概念来自于生物学

多层卷积

利用一次卷积运算(哪怕是多个卷积核)提取的特征往往是局部的，难以提取出比较全局的特征，因此需要在一层卷积基础上继续做卷积计算 ，这也就是多层卷积，例如下面这个示意图：

这实际上有四层卷积、三层池化、加上一层全连接，经过这些计算后得出的特征再利用常规的机器学习分类算法(如soft-max)做分类训练。上面这个过程是一个真实的人脸识别的卷积神经网络。

池化

上面讲到了池化，池化是一种降维的方法。按照卷积计算得出的特征向量维度大的惊人，不但会带来非常大的计算量，而且容易出现过拟合，解决过拟合的办法就是让模型尽量“泛化”，也就是再“模糊”一点，那么一种方法就是把图像中局部区域的特征做一个平滑压缩处理，这源于局部图像一些特征的相似性(即局部相关性原理)。

具体做法就是对卷积计算得出的特征在局部范围内算出一个平均值(或者取最大值、或者取随机采样值)作为特征值，那么这个局部范围(假如是10*10)，就被压缩成了1*1，压缩了100倍，这样虽然更“模糊”了，但是也更“泛化”了。通过取平均值来池化叫做平均池化，通过取最大值来池化叫做最大池化。

卷积神经网络训练过程

上面讲解了卷积神经网络的原理，那么既然是深度学习，要学习的参数在哪里呢？

上面我们讲的卷积核中的因子(×1或×0)其实就是需要学习的参数，也就是卷积核矩阵元素的值就是参数值。一个特征如果有9个值，1000个特征就有900个值，再加上多个层，需要学习的参数还是比较多的。

和多层神经网络(见我的另外一篇文章《机器学习教程 十二-神经网络模型的原理》)一样，为了方便用链式求导法则更新参数，我们设计sigmoid函数作为激活函数，我们同时也发现卷积计算实际上就是多层神经网络中的Wx矩阵乘法，同时要加上一个偏执变量b，那么前向传到的计算过程就是：

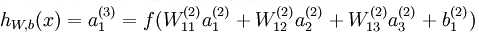
如果有更多层，计算方法相同

因为是有监督学习，所以模型计算出的y'和观察值y之间的偏差用于更新模型参数，反向传导的计算方法参考《机器学习教程 十二-神经网络模型的原理》中的反向传导算法：

参数更新公式是：

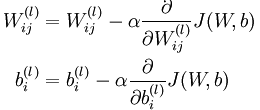
偏导计算公式是：

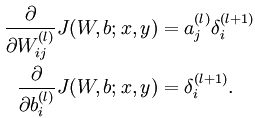
其中a的计算公式是：

残差δ的计算公式是：

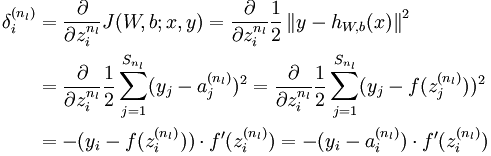
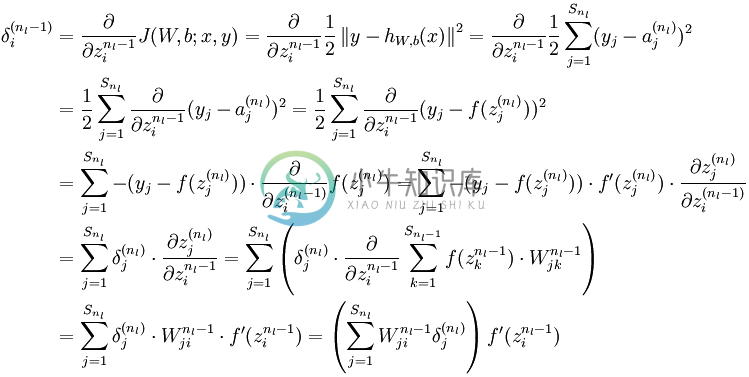
上面是输出层残差的推导公式和计算方法，下面是隐藏层残差的推导公式和计算方法