PyTorch搭建多项式回归模型（三）

PyTorch基础入门三：PyTorch搭建多项式回归模型 

1）理论简介

对于一般的线性回归模型，由于该函数拟合出来的是一条直线，所以精度欠佳，我们可以考虑多项式回归来拟合更多的模型。所谓多项式回归，其本质也是线性回归。也就是说，我们采取的方法是，提高每个属性的次数来增加维度数。比如，请看下面这样的例子：

如果我们想要拟合方程：

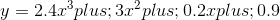
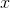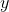对于输入变量和输出值，我们只需要增加其平方项、三次方项系数即可。所以，我们可以设置如下参数方程：

可以看到，上述方程与线性回归方程并没有本质区别。所以我们可以采用线性回归的方式来进行多项式的拟合。下面请看代码部分。

2）代码实现

当然最先要做的就是导包了，下面需要说明的只有一个：itertools中的count，这个是用来记数用的，其可以记数到无穷，第一个参数是记数的起始值，第二个参数是步长。其内部实现相当于如下代码：

def count(firstval=0, step=1):
 x = firstval
 while 1:
 yield x
 x += step

下面是导包部分代码，这里定义了一个常量POLY_DEGREE = 3用来指定多项式最高次数。

from itertools import count
import torch
import torch.autograd
import torch.nn.functional as F
 
POLY_DEGREE = 3

然后我们需要将数据处理成矩阵的形式：

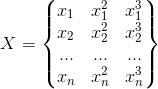
在PyTorch里面使用torch.cat()函数来实现Tensor的拼接：

def make_features(x):
 """Builds features i.e. a matrix with columns [x, x^2, x^3, x^4]."""
 x = x.unsqueeze(1)
 return torch.cat([x ** i for i in range(1, POLY_DEGREE+1)], 1)

对于输入的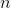个数据，我们将其扩展成上面矩阵所示的样子。

然后定义出我们需要拟合的多项式，可以随机抽取一个多项式来作为我们的目标多项式。当然，系数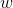和偏置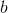确定了，多项式也就确定了：

W_target = torch.randn(POLY_DEGREE, 1)
b_target = torch.randn(1)
 
def f(x):
 """Approximated function."""
 return x.mm(W_target) + b_target.item()

这里的权重已经定义好了，x.mm(W_target)表示做矩阵乘法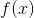，就是每次输入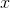一个得到一个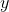的真实函数。

在训练的时候我们需要采样一些点，可以随机生成一批数据来得到训练集。下面的函数可以让我们每次取batch_size这么多个数据，然后将其转化为矩阵形式，再把这个值通过函数之后的结果也返回作为真实的输出值：

def get_batch(batch_size=32):
 """Builds a batch i.e. (x, f(x)) pair."""
 random = torch.randn(batch_size)
 x = make_features(random)
 y = f(x)
 return x, y

接下来我们需要定义模型，这里采用一种简写的方式定义模型，torch.nn.Linear()表示定义一个线性模型，这里定义了是输入值和目标参数的行数一致（和POLY_DEGREE一致，本次实验中为3），输出值为1的模型。

# Define model
fc = torch.nn.Linear(W_target.size(0), 1)

下面开始训练模型，训练的过程让其不断优化，直到随机取出的batch_size个点中计算出来的均方误差小于0.001为止。

for batch_idx in count(1):
 # Get data
 batch_x, batch_y = get_batch()
 
 # Reset gradients
 fc.zero_grad()
 
 # Forward pass
 output = F.smooth_l1_loss(fc(batch_x), batch_y)
 loss = output.item()
 
 # Backward pass
 output.backward()
 
 # Apply gradients
 for param in fc.parameters():
 param.data.add_(-0.1 * param.grad.data)
 
 # Stop criterion
 if loss < 1e-3:
 break

这样就已经训练出了我们的多项式回归模型，为了方便观察，定义了如下打印函数来打印出我们拟合的多项式表达式：

def poly_desc(W, b):
 """Creates a string description of a polynomial."""
 result = 'y = '
 for i, w in enumerate(W):
 result += '{:+.2f} x^{} '.format(w, len(W) - i)
 result += '{:+.2f}'.format(b[0])
 return result
 
print('Loss: {:.6f} after {} batches'.format(loss, batch_idx))
print('==> Learned function:\t' + poly_desc(fc.weight.view(-1), fc.bias))
print('==> Actual function:\t' + poly_desc(W_target.view(-1), b_target))

程序运行结果如下图所示：

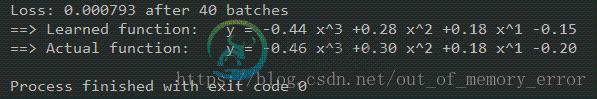
可以看出，真实的多项式表达式和我们拟合的多项式十分接近。现实世界中很多问题都不是简单的线性回归，涉及到很多复杂的非线性模型。但是我们可以在其特征量上进行研究，改变或者增加其特征，从而将非线性问题转化为线性问题来解决，这种处理问题的思路是我们从多项式回归的算法中应该汲取到的。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。