PyTorch上搭建简单神经网络实现回归和分类的示例

本文介绍了PyTorch上搭建简单神经网络实现回归和分类的示例，分享给大家，具体如下：

一、PyTorch入门

1. 安装方法

登录PyTorch官网，http://pytorch.org，可以看到以下界面：

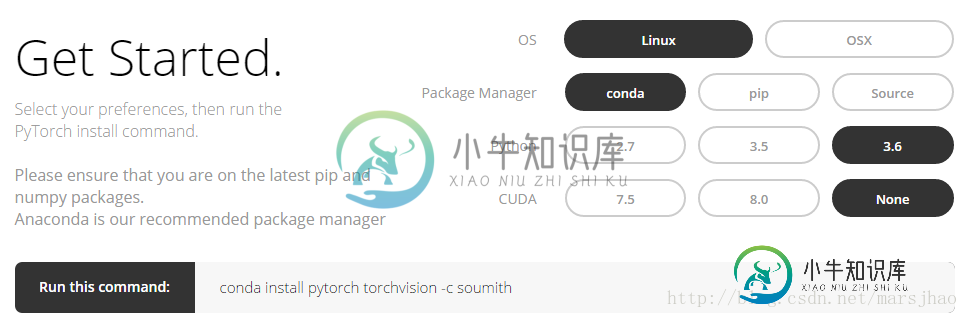
按上图的选项选择后即可得到Linux下conda指令：

conda install pytorch torchvision -c soumith

目前PyTorch仅支持MacOS和Linux，暂不支持Windows。安装 PyTorch 会安装两个模块，一个是torch，一个 torchvision, torch 是主模块，用来搭建神经网络的，torchvision 是辅模块，有数据库，还有一些已经训练好的神经网络等着你直接用，比如 (VGG, AlexNet, ResNet)。

2. Numpy与Torch

torch_data = torch.from_numpy(np_data)可以将numpy(array)格式转换为torch(tensor)格式；torch_data.numpy()又可以将torch的tensor格式转换为numpy的array格式。注意Torch的Tensor和numpy的array会共享他们的存储空间，修改一个会导致另外的一个也被修改。

对于1维（1-D）的数据，numpy是以行向量的形式打印输出，而torch是以列向量的形式打印输出的。

其他例如sin, cos, abs,mean等numpy中的函数在torch中用法相同。需要注意的是，numpy中np.matmul(data, data)和data.dot(data)矩阵相乘会得到相同结果；torch中torch.mm(tensor, tensor)是矩阵相乘的方法，得到一个矩阵，tensor.dot(tensor)会把tensor转换为1维的tensor，然后逐元素相乘后求和，得到与一个实数。

相关代码：

import torch 
import numpy as np 
 
np_data = np.arange(6).reshape((2, 3)) 
torch_data = torch.from_numpy(np_data) # 将numpy(array)格式转换为torch(tensor)格式 
tensor2array = torch_data.numpy()  
print( 
  '\nnumpy array:\n', np_data,  
  '\ntorch tensor:', torch_data,  
  '\ntensor to array:\n', tensor2array,  
) # torch数据格式在print的时候前后自动添加换行符 
 
# abs 
data = [-1, -2, 2, 2] 
tensor = torch.FloatTensor(data)  
print( 
  '\nabs', 
  '\nnumpy: \n', np.abs(data),     
  '\ntorch: ', torch.abs(tensor)  
) # 1维的数据，numpy是行向量形式显示，torch是列向量形式显示 
 
# sin 
print( 
  '\nsin', 
  '\nnumpy: \n', np.sin(data),    
  '\ntorch: ', torch.sin(tensor)  
) 
 
# mean 
print( 
  '\nmean', 
  '\nnumpy: ', np.mean(data),   
  '\ntorch: ', torch.mean(tensor)  
) 
 
# 矩阵相乘 
data = [[1,2], [3,4]] 
tensor = torch.FloatTensor(data)  
 
print( 
  '\nmatrix multiplication (matmul)', 
  '\nnumpy: \n', np.matmul(data, data),   
  '\ntorch: ', torch.mm(tensor, tensor)  
) 
 
data = np.array(data) 
print( 
  '\nmatrix multiplication (dot)', 
  '\nnumpy: \n', data.dot(data),    
  '\ntorch: ', tensor.dot(tensor)   
) 

3. Variable

PyTorch中的神经网络来自于autograd包，autograd包提供了Tensor所有操作的自动求导方法。

autograd.Variable这是这个包中最核心的类。可以将Variable理解为一个装有tensor的容器，它包装了一个Tensor，并且几乎支持所有的定义在其上的操作。一旦完成运算，便可以调用 .backward()来自动计算出所有的梯度。也就是说只有把tensor置于Variable中，才能在神经网络中实现反向传递、自动求导等运算。

可以通过属性 .data 来访问原始的tensor，而关于这一Variable的梯度则可通过 .grad属性查看。

相关代码：

import torch 
from torch.autograd import Variable 
 
tensor = torch.FloatTensor([[1,2],[3,4]]) 
variable = Variable(tensor, requires_grad=True) 
# 打印展示Variable类型 
print(tensor) 
print(variable) 
 
t_out = torch.mean(tensor*tensor) # 每个元素的^ 2 
v_out = torch.mean(variable*variable) 
print(t_out) 
print(v_out) 
 
v_out.backward() # Variable的误差反向传递 
 
# 比较Variable的原型和grad属性、data属性及相应的numpy形式 
print('variable:\n', variable) 
# v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤 
# 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2 
print('variable.grad:\n', variable.grad) # Variable的梯度 
print('variable.data:\n', variable.data) # Variable的数据 
print(variable.data.numpy()) #Variable的数据的numpy形式 

部分输出结果：

variable:
Variable containing:
1 2
3 4
[torch.FloatTensor of size 2x2]
variable.grad:
Variable containing:
0.5000 1.0000
1.5000 2.0000
[torch.FloatTensor of size 2x2]
variable.data:
1 2
3 4
[torch.FloatTensor of size 2x2]
[[ 1. 2.]
[ 3. 4.]]

4. 激励函数activationfunction

Torch的激励函数都在torch.nn.functional中，relu,sigmoid, tanh, softplus都是常用的激励函数。

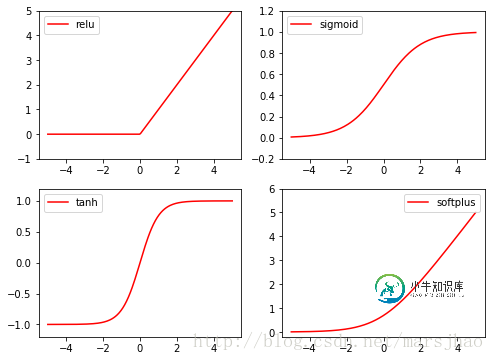
相关代码：

import torch 
import torch.nn.functional as F 
from torch.autograd import Variable 
import matplotlib.pyplot as plt 
 
x = torch.linspace(-5, 5, 200) 
x_variable = Variable(x) #将x放入Variable 
x_np = x_variable.data.numpy() 
 
# 经过4种不同的激励函数得到的numpy形式的数据结果 
y_relu = F.relu(x_variable).data.numpy() 
y_sigmoid = F.sigmoid(x_variable).data.numpy() 
y_tanh = F.tanh(x_variable).data.numpy() 
y_softplus = F.softplus(x_variable).data.numpy() 
 
plt.figure(1, figsize=(8, 6)) 
 
plt.subplot(221) 
plt.plot(x_np, y_relu, c='red', label='relu') 
plt.ylim((-1, 5)) 
plt.legend(loc='best') 
 
plt.subplot(222) 
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid') 
plt.ylim((-0.2, 1.2)) 
plt.legend(loc='best') 
 
plt.subplot(223) 
plt.plot(x_np, y_tanh, c='red', label='tanh') 
plt.ylim((-1.2, 1.2)) 
plt.legend(loc='best') 
 
plt.subplot(224) 
plt.plot(x_np, y_softplus, c='red', label='softplus') 
plt.ylim((-0.2, 6)) 
plt.legend(loc='best') 
 
plt.show() 

二、PyTorch实现回归

先看完整代码：

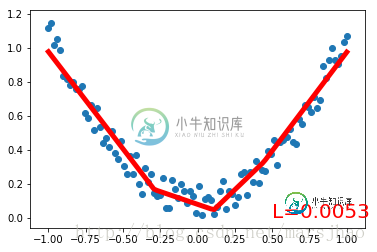
import torch 
from torch.autograd import Variable 
import torch.nn.functional as F 
import matplotlib.pyplot as plt 
 
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # 将1维的数据转换为2维数据 
y = x.pow(2) + 0.2 * torch.rand(x.size()) 
 
# 将tensor置入Variable中 
x, y = Variable(x), Variable(y) 
 
#plt.scatter(x.data.numpy(), y.data.numpy()) 
#plt.show() 
 
# 定义一个构建神经网络的类 
class Net(torch.nn.Module): # 继承torch.nn.Module类 
  def __init__(self, n_feature, n_hidden, n_output): 
    super(Net, self).__init__() # 获得Net类的超类（父类）的构造方法 
    # 定义神经网络的每层结构形式 
    # 各个层的信息都是Net类对象的属性 
    self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出 
    self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出 
 
  # 将各层的神经元搭建成完整的神经网络的前向通路 
  def forward(self, x): 
    x = F.relu(self.hidden(x)) # 对隐藏层的输出进行relu激活 
    x = self.predict(x) 
    return x 
 
# 定义神经网络 
net = Net(1, 10, 1) 
print(net) # 打印输出net的结构 
 
# 定义优化器和损失函数 
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) # 传入网络参数和学习率 
loss_function = torch.nn.MSELoss() # 最小均方误差 
 
# 神经网络训练过程 
plt.ion()  # 动态学习过程展示 
plt.show() 
 
for t in range(300): 
  prediction = net(x) # 把数据x喂给net，输出预测值 
  loss = loss_function(prediction, y) # 计算两者的误差，要注意两个参数的顺序 
  optimizer.zero_grad() # 清空上一步的更新参数值 
  loss.backward() # 误差反相传播，计算新的更新参数值 
  optimizer.step() # 将计算得到的更新值赋给net.parameters() 
 
  # 可视化训练过程 
  if (t+1) % 10 == 0: 
    plt.cla() 
    plt.scatter(x.data.numpy(), y.data.numpy()) 
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5) 
    plt.text(0.5, 0, 'L=%.4f' % loss.data[0], fontdict={'size': 20, 'color': 'red'}) 
    plt.pause(0.1) 

首先创建一组带噪声的二次函数拟合数据，置于Variable中。定义一个构建神经网络的类Net，继承torch.nn.Module类。Net类的构造方法中定义输入神经元、隐藏层神经元、输出神经元数量的参数，通过super()方法获得Net父类的构造方法，以属性的方式定义Net的各个层的结构形式；定义Net的forward()方法将各层的神经元搭建成完整的神经网络前向通路。

定义好Net类后，定义神经网络实例，Net类实例可以直接print打印输出神经网络的结构信息。接着定义神经网络的优化器和损失函数。定义好这些后就可以进行训练了。optimizer.zero_grad()、loss.backward()、optimizer.step()分别是清空上一步的更新参数值、进行误差的反向传播并计算新的更新参数值、将计算得到的更新值赋给net.parameters()。循环迭代训练过程。

运行结果：

Net (

 (hidden): Linear (1 -> 10)

 (predict): Linear (10 -> 1)

)

三、PyTorch实现简单分类

完整代码：

import torch 
from torch.autograd import Variable 
import torch.nn.functional as F 
import matplotlib.pyplot as plt 
 
# 生成数据 
# 分别生成2组各100个数据点，增加正态噪声，后标记以y0=0 y1=1两类标签，最后cat连接到一起 
n_data = torch.ones(100,2) 
# torch.normal(means, std=1.0, out=None) 
x0 = torch.normal(2*n_data, 1) # 以tensor的形式给出输出tensor各元素的均值，共享标准差 
y0 = torch.zeros(100) 
x1 = torch.normal(-2*n_data, 1) 
y1 = torch.ones(100) 
 
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # 组装（连接） 
y = torch.cat((y0, y1), 0).type(torch.LongTensor) 
 
# 置入Variable中 
x, y = Variable(x), Variable(y) 
 
class Net(torch.nn.Module): 
  def __init__(self, n_feature, n_hidden, n_output): 
    super(Net, self).__init__() 
    self.hidden = torch.nn.Linear(n_feature, n_hidden) 
    self.out = torch.nn.Linear(n_hidden, n_output) 
 
  def forward(self, x): 
    x = F.relu(self.hidden(x)) 
    x = self.out(x) 
    return x 
 
net = Net(n_feature=2, n_hidden=10, n_output=2) 
print(net) 
 
optimizer = torch.optim.SGD(net.parameters(), lr=0.012) 
loss_func = torch.nn.CrossEntropyLoss() 
 
plt.ion() 
plt.show() 
 
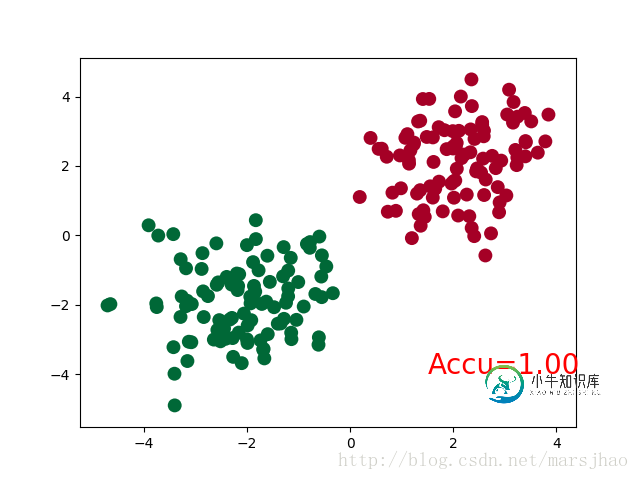
for t in range(100): 
  out = net(x) 
  loss = loss_func(out, y) # loss是定义为神经网络的输出与样本标签y的差别，故取softmax前的值 
 
  optimizer.zero_grad() 
  loss.backward() 
  optimizer.step() 
 
  if t % 2 == 0: 
    plt.cla() 
    # 过了一道 softmax 的激励函数后的最大概率才是预测值 
    # torch.max既返回某个维度上的最大值，同时返回该最大值的索引值 
    prediction = torch.max(F.softmax(out), 1)[1] # 在第1维度取最大值并返回索引值 
    pred_y = prediction.data.numpy().squeeze() 
    target_y = y.data.numpy() 
    plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn') 
    accuracy = sum(pred_y == target_y)/200 # 预测中有多少和真实值一样 
    plt.text(1.5, -4, 'Accu=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'}) 
    plt.pause(0.1) 
 
plt.ioff() 
plt.show() 

神经网络结构部分的Net类与前文的回归部分的结构相同。

需要注意的是，在循环迭代训练部分，out定义为神经网络的输出结果，计算误差loss时不是使用one-hot形式的，loss是定义在out与y上的torch.nn.CrossEntropyLoss()，而预测值prediction定义为out经过Softmax后（将结果转化为概率值）的结果。

运行结果：

Net (

 (hidden): Linear (2 -> 10)

  (out):Linear (10 -> 2)

)

四、补充知识

1. super()函数

在定义Net类的构造方法的时候，使用了super(Net,self).__init__()语句，当前的类和对象作为super函数的参数使用，这条语句的功能是使Net类的构造方法获得其超类（父类）的构造方法，不影响对Net类单独定义构造方法，且不必关注Net类的父类到底是什么，若需要修改Net类的父类时只需修改class语句中的内容即可。

2. torch.normal()

torch.normal()可分为三种情况：（1）torch.normal(means,std, out=None)中means和std都是Tensor，两者的形状可以不必相同，但Tensor内的元素数量必须相同，一一对应的元素作为输出的各元素的均值和标准差；（2）torch.normal(mean=0.0, std, out=None)中mean是一个可定义的float，各个元素共享该均值；（3）torch.normal(means,std=1.0, out=None)中std是一个可定义的float，各个元素共享该标准差。

3. torch.cat(seq, dim=0)

torch.cat可以将若干个Tensor组装连接起来，dim指定在哪个维度上进行组装。

4. torch.max()

（1）torch.max(input)→ float

input是tensor，返回input中的最大值float。

（2）torch.max(input,dim, keepdim=True, max=None, max_indices=None) -> (Tensor, LongTensor)

同时返回指定维度=dim上的最大值和该最大值在该维度上的索引值。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。