PyTorch线性回归和逻辑回归实战示例

茅星华

2023-03-14

本文向大家介绍PyTorch线性回归和逻辑回归实战示例，包括了PyTorch线性回归和逻辑回归实战示例的使用技巧和注意事项，需要的朋友参考一下

线性回归实战

使用PyTorch定义线性回归模型一般分以下几步：

1.设计网络架构
2.构建损失函数(loss)和优化器(optimizer)
3.训练(包括前馈(forward)、反向传播(backward)、更新模型参数(update))

#author:yuquanle
#data:2018.2.5
#Study of LinearRegression use PyTorch

import torch
from torch.autograd import Variable

# train data
x_data = Variable(torch.Tensor([[1.0], [2.0], [3.0]]))
y_data = Variable(torch.Tensor([[2.0], [4.0], [6.0]]))

class Model(torch.nn.Module):
  def __init__(self):
    super(Model, self).__init__()
    self.linear = torch.nn.Linear(1, 1) # One in and one out

  def forward(self, x):
    y_pred = self.linear(x)
    return y_pred

# our model
model = Model()

criterion = torch.nn.MSELoss(size_average=False) # Defined loss function
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # Defined optimizer

# Training: forward, loss, backward, step
# Training loop
for epoch in range(50):
  # Forward pass
  y_pred = model(x_data)

  # Compute loss
  loss = criterion(y_pred, y_data)
  print(epoch, loss.data[0])

  # Zero gradients
  optimizer.zero_grad()
  # perform backward pass
  loss.backward()
  # update weights
  optimizer.step()

# After training
hour_var = Variable(torch.Tensor([[4.0]]))
print("predict (after training)", 4, model.forward(hour_var).data[0][0])

迭代十次打印结果：

0 123.87958526611328
1 55.19491195678711
2 24.61777114868164
3 11.005026817321777
4 4.944361686706543
5 2.2456750869750977
6 1.0436556339263916
7 0.5079189538955688
8 0.2688019871711731
9 0.16174012422561646
predict (after training) 4 7.487752914428711

loss还在继续下降，此时输入4得到的结果还不是预测的很准

当迭代次数设置为50时：

0 35.38422393798828
5 0.6207122802734375
10 0.012768605723977089
15 0.0020055510103702545
20 0.0016929294215515256
25 0.0015717096393927932
30 0.0014619173016399145
35 0.0013598509831354022
40 0.0012649153359234333
45 0.00117658288218081
50 0.001094428705982864
predict (after training) 4 8.038028717041016

此时，函数已经拟合比较好了

再运行一次：

0 159.48605346679688
5 2.827991485595703
10 0.08624256402254105
15 0.03573693335056305
20 0.032463930547237396
25 0.030183646827936172
30 0.02807590737938881
35 0.026115568354725838
40 0.02429218217730522
45 0.022596003487706184
50 0.0210183784365654
predict (after training) 4 7.833342552185059

发现同为迭代50次，但是当输入为4时，结果不同，感觉应该是使用pytorch定义线性回归模型时:
torch.nn.Linear(1, 1)，只需要知道输入和输出维度，里面的参数矩阵是随机初始化的(具体是不是随机的还是按照一定约束条件初始化的我不确定)，所有每次计算loss会下降到不同的位置(模型的参数更新从而也不同)，导致结果不一样。

逻辑回归实战

线性回归是解决回归问题的，逻辑回归和线性回归很像，但是它是解决分类问题的(一般二分类问题:0 or 1)。也可以多分类问题(用softmax可以实现)。

使用pytorch实现逻辑回归的基本过程和线性回归差不多，但是有以下几个区别：

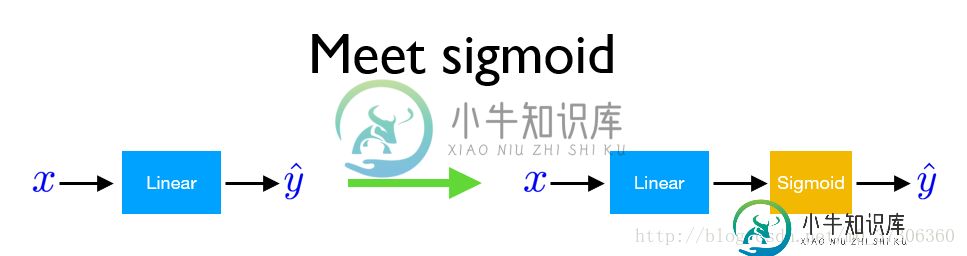
下面为sigmoid函数：

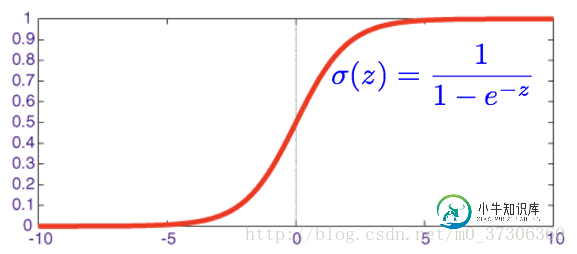
在逻辑回归中，我们预测如果当输出大于0.5时，y=1;否则y=0。

损失函数一般采用交叉熵loss:

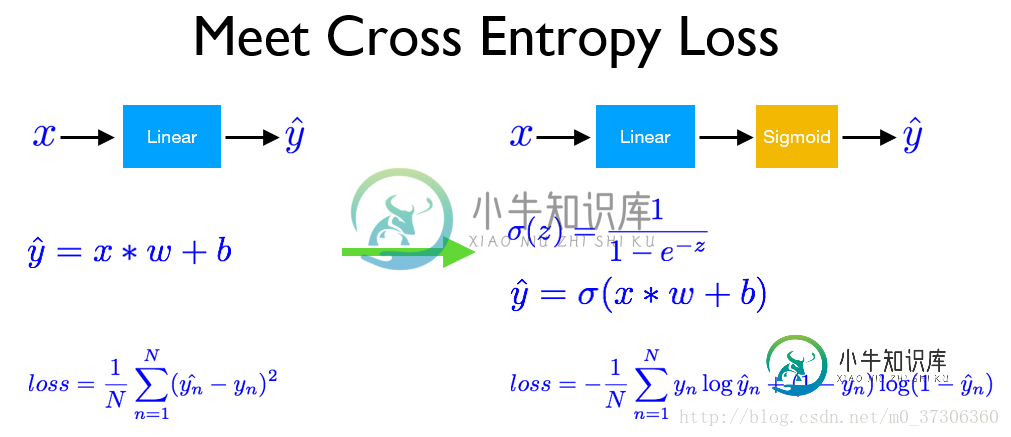
# date:2018.2.6
# LogisticRegression

import torch
from torch.autograd import Variable

x_data = Variable(torch.Tensor([[0.6], [1.0], [3.5], [4.0]]))
y_data = Variable(torch.Tensor([[0.], [0.], [1.], [1.]]))

class Model(torch.nn.Module):
  def __init__(self):
    super(Model, self).__init__()
    self.linear = torch.nn.Linear(1, 1) # One in one out
    self.sigmoid = torch.nn.Sigmoid()

  def forward(self, x):
    y_pred = self.sigmoid(self.linear(x))
    return y_pred

# Our model
model = Model()

# Construct loss function and optimizer
criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# Training loop
for epoch in range(500):
  # Forward pass
  y_pred = model(x_data)

  # Compute loss
  loss = criterion(y_pred, y_data)
  if epoch % 20 == 0:
    print(epoch, loss.data[0])

  # Zero gradients
  optimizer.zero_grad()
  # Backward pass
  loss.backward()
  # update weights
  optimizer.step()

# After training
hour_var = Variable(torch.Tensor([[0.5]]))
print("predict (after training)", 0.5, model.forward(hour_var).data[0][0])
hour_var = Variable(torch.Tensor([[7.0]]))
print("predict (after training)", 7.0, model.forward(hour_var).data[0][0])

输入结果：

0 0.9983477592468262
20 0.850886881351471
40 0.7772406339645386
60 0.7362991571426392
80 0.7096697092056274
100 0.6896909475326538
120 0.6730546355247498
140 0.658246636390686
160 0.644534170627594
180 0.6315458416938782
200 0.6190851330757141
220 0.607043981552124
240 0.5953611731529236
260 0.5840001106262207
280 0.5729377269744873
300 0.5621585845947266
320 0.5516515970230103
340 0.5414079427719116
360 0.5314203500747681
380 0.5216821432113647
400 0.512187123298645
420 0.5029295086860657
440 0.49390339851379395
460 0.4851033389568329
480 0.47652381658554077
predict (after training) 0.5 0.49599987268447876
predict (after training) 7.0 0.9687209129333496

Process finished with exit code 0

训练完模型之后，输入新的数据0.5，此时输出小于0.5，则为0类别，输入7输出大于0.5，则为1类别。使用softmax做多分类时，那个维度的数值大，则为那个数值所对应位置的类别。

更深更宽的网络

前面的例子都是浅层输入为一维的网络，如果需要更深更宽的网络，使用pytorch也可以很好的实现，以逻辑回归为例：
当输入x的维度很大时，需要更宽的网络:

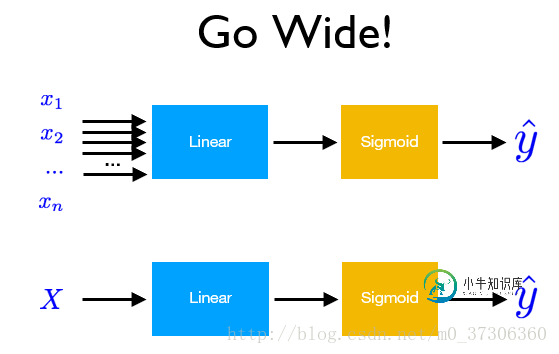
更深的网络：

采用下面数据集(下载地址:https://github.com/hunkim/PyTorchZeroToAll/tree/master/data)

输入维度为八。

#author:yuquanle
#date:2018.2.7
#Deep and Wide


import torch
from torch.autograd import Variable
import numpy as np

xy = np.loadtxt('./data/diabetes.csv', delimiter=',', dtype=np.float32)
x_data = Variable(torch.from_numpy(xy[:, 0:-1]))
y_data = Variable(torch.from_numpy(xy[:, [-1]]))

#print(x_data.data.shape)
#print(y_data.data.shape)

class Model(torch.nn.Module):
  def __init__(self):
    super(Model, self).__init__()
    self.l1 = torch.nn.Linear(8, 6)
    self.l2 = torch.nn.Linear(6, 4)
    self.l3 = torch.nn.Linear(4, 1)
    self.sigmoid = torch.nn.Sigmoid()

  def forward(self, x):
    x = self.sigmoid(self.l1(x))
    x = self.sigmoid(self.l2(x))
    y_pred = self.sigmoid(self.l3(x))
    return y_pred

# our model
model = Model()

cirterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)

hour_var = Variable(torch.Tensor([[-0.294118,0.487437,0.180328,-0.292929,0,0.00149028,-0.53117,-0.0333333]]))
print("(Before training)", model.forward(hour_var).data[0][0])

# Training loop
for epoch in range(1000):
  y_pred = model(x_data)
  # y_pred,y_data不能写反(因为损失函数为交叉熵loss)
  loss = cirterion(y_pred, y_data)
  optimizer.zero_grad()
  loss.backward()
  optimizer.step()
  if epoch % 50 == 0:
    print(epoch, loss.data[0])


# After training
hour_var = Variable(torch.Tensor([[-0.294118,0.487437,0.180328,-0.292929,0,0.00149028,-0.53117,-0.0333333]]))
print("predict (after training)", model.forward(hour_var).data[0][0])

结果：

(Before training) 0.5091859698295593
0 0.6876295208930969
50 0.6857835650444031
100 0.6840178370475769
150 0.6823290586471558
200 0.6807141900062561
250 0.6791688203811646
300 0.6776910424232483
350 0.6762782335281372
400 0.6749269366264343
450 0.6736343502998352
500 0.6723981499671936
550 0.6712161302566528
600 0.6700847744941711
650 0.6690039038658142
700 0.667969822883606
750 0.666980504989624
800 0.6660353541374207
850 0.6651310324668884
900 0.664265513420105
950 0.6634389758110046
predict (after training) 0.5618339776992798
Process finished with exit code 0

参考:

1.https://github.com/hunkim/PyTorchZeroToAll

2.http://pytorch.org/tutorials/beginner/deep_learning_60min_blitz.html

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。

PyTorch线性回归和逻辑回归实战示例

相关阅读

相关文章

相关问答

相关工具

相关文档