c# 模拟线性回归的示例

最近刚开始接触机器学习，在这里使用c#模拟一元线性回归，先上图看效果

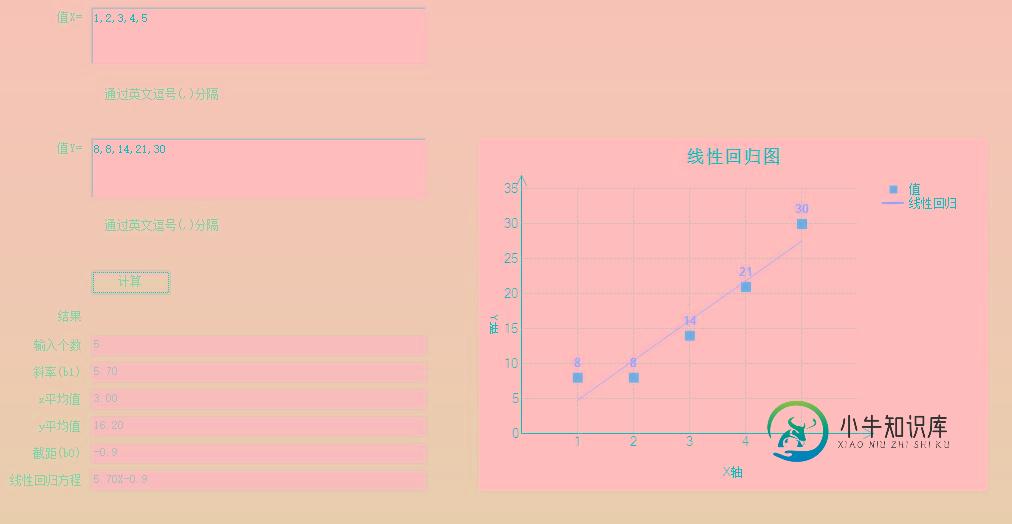
因为源码中有一些控件是自己封装的，所以就不上传可运行的程序集了，贴出核心代码，以供参考，如有不对，请多多给予建议

private void ryButtonX1_Click(object sender, EventArgs e)
    {
      string[] xnum = richTextBox1.Text.Trim().Split(',');//x值
      string[] ynum = richTextBox2.Text.Trim().Split(',');//y值
      if (xnum.Length != ynum.Length)
      {
        MessageBox.Show("输入数据有误!");
        return;
      }
      ryTextBoxX1.Text = xnum.Length+"";//个数
      decimal xsum = 0;//x值求和
      decimal ysum = 0;//y值求和
      for(int i = 0; i < xnum.Length; i++)
      {
        xsum = xsum + ConvertExtend.ToDecimal(xnum[i],0);
        ysum = ysum + ConvertExtend.ToDecimal(ynum[i], 0);
      }
      decimal xAve = ConvertExtend.ToDecimal(xsum / xnum.Length, 0);//x平均值
      decimal yAve = ConvertExtend.ToDecimal(ysum / xnum.Length, 0);//y平均值

      ryTextBoxX3.Text = string.Format("{0:N}", xAve);//保留两位小数
      ryTextBoxX4.Text = string.Format("{0:N}", yAve);

      decimal molecule = 0;//分子
      decimal Denominator = 0;//分母
      for (int i = 0; i < xnum.Length; i++)
      {
        molecule = molecule + (ConvertExtend.ToDecimal(xnum[i], 0) - xAve) * (ConvertExtend.ToDecimal(ynum[i], 0) - yAve);
        Denominator = Denominator+(ConvertExtend.ToDecimal(xnum[i], 0) - xAve) * (ConvertExtend.ToDecimal(xnum[i], 0) - xAve);
      }
      ryTextBoxX2.Text = string.Format("{0:N}", molecule / Denominator);//斜率
      ryTextBoxX5.Text = (yAve - (molecule / Denominator) * xAve)+"";//截距

      if (ConvertExtend.ToDecimal(ryTextBoxX5.Text, 0) < 0)
      {
        ryTextBoxX6.Text = ryTextBoxX2.Text + "X" + ryTextBoxX5.Text;
      }else
      {
        ryTextBoxX6.Text = ryTextBoxX2.Text + "X+" + ryTextBoxX5.Text;
      }

      #region 画点
      chartLabTrend.ChartAreas[0].AxisX.CustomLabels.Clear();
      List<decimal?> lx = new List<decimal?>();
      List<decimal?> l1 = new List<decimal?>();
      for (int i = 1; i <= xnum.Length; i++)
      {
        CustomLabel label1 = new CustomLabel();
        if (xnum[i - 1] != "")
        {
          label1.Text = ConvertExtend.ToDecimal(xnum[i - 1],0).ToString();
          label1.ToPosition = i * 2;
          chartLabTrend.ChartAreas[0].AxisX.CustomLabels.Add(label1);
          label1.GridTicks = GridTickTypes.Gridline;
          lx.Add(i);
          if (ynum[i - 1] == null)
          {
            l1.Add(null);
          }
          else
          {
            l1.Add(ConvertExtend.ToDecimal(ynum[i - 1],0));
          }
        }
      }
      chartLabTrend.Series[0].Points.DataBindXY(lx, l1);
      #endregion

      #region 画线
      chartLabTrend.ChartAreas[0].AxisX.CustomLabels.Clear();
      List<decimal?> lx1 = new List<decimal?>();
      List<decimal?> l11 = new List<decimal?>();
      for (int i = 1; i <= xnum.Length; i++)
      {
        CustomLabel label2 = new CustomLabel();
        if (xnum[i - 1] != "")
        {
          label2.Text = ConvertExtend.ToDecimal(xnum[i - 1], 0).ToString();
          label2.ToPosition = i * 2;
          chartLabTrend.ChartAreas[0].AxisX.CustomLabels.Add(label2);
          label2.GridTicks = GridTickTypes.Gridline;
          lx1.Add(i);
          if (ynum[i - 1] == null)
          {
            l11.Add(null);
          }
          else
          {
            l11.Add(ConvertExtend.ToDecimal(ConvertExtend.ToDecimal(xnum[i - 1],0)*molecule / Denominator
              + ConvertExtend.ToDecimal(ryTextBoxX5.Text,0), 0));
          }
        }
      }
      chartLabTrend.Series[1].Points.DataBindXY(lx1, l11);
      #endregion

    }

以上就是c# 模拟线性回归的示例的详细内容，更多关于c# 模拟线性回归的资料请关注小牛知识库其它相关文章！