登录
目录
当前位置： 首页 > 文档资料 > Spark 机器学习算法研究和源码分析 >

线性模型 - 线性回归

优质
小牛编辑
137浏览
2023-12-01

  回归问题的条件或者说前提是

  • 1） 收集的数据
  • 2） 假设的模型，即一个函数，这个函数里含有未知的参数，通过学习，可以估计出参数。然后利用这个模型去预测/分类新的数据。

1 线性回归的概念

  线性回归假设特征和结果都满足线性。即不大于一次方。收集的数据中，每一个分量，就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数，向量表示形式：

1.1

  这个就是一个组合问题，已知一些数据，如何求里面的未知参数，给出一个最优解。 一个线性矩阵方程，直接求解，很可能无法直接求解。有唯一解的数据集，微乎其微。

  基本上都是解不存在的超定方程组。因此，需要退一步，将参数求解问题，转化为求最小误差问题，求出一个最接近的解，这就是一个松弛求解。

  在回归问题中，线性最小二乘是最普遍的求最小误差的形式。它的损失函数就是二乘损失。如下公式（1）所示：

1.2

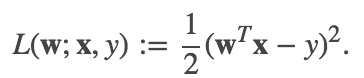
  根据使用的正则化类型的不同，回归算法也会有不同。普通最小二乘和线性最小二乘回归不使用正则化方法。ridge回归使用L2正则化，lasso回归使用L1正则化。

2 线性回归源码分析

2.1 实例

  1. import org.apache.spark.ml.regression.LinearRegression
  3. // 加载数据
  4. val training = spark.read.format("libsvm")
  5.   .load("data/mllib/sample_linear_regression_data.txt")
  7. val lr = new LinearRegression()
  8.   .setMaxIter(10)
  9.   .setRegParam(0.3)
  10.   .setElasticNetParam(0.8)
  12. // 训练模型
  13. val lrModel = lr.fit(training)
  15. // 打印线性回归的系数和截距
  16. println(s"Coefficients: ${lrModel.coefficients} Intercept: ${lrModel.intercept}")
  18. // 打印统计信息
  19. val trainingSummary = lrModel.summary
  20. println(s"numIterations: ${trainingSummary.totalIterations}")
  21. println(s"objectiveHistory: [${trainingSummary.objectiveHistory.mkString(",")}]")
  22. trainingSummary.residuals.show()
  23. println(s"RMSE: ${trainingSummary.rootMeanSquaredError}")
  24. println(s"r2: ${trainingSummary.r2}")

2.2 代码实现

2.2.1 参数配置

  根据上面的例子，我们先看看线性回归可以配置的参数。

  1. // 正则化参数，默认为0，对应于优化算法中的lambda
  2. def setRegParam(value: Double): this.type = set(regParam, value)
  3. setDefault(regParam -> 0.0)
  5. // 是否使用截距，默认使用
  6. def setFitIntercept(value: Boolean): this.type = set(fitIntercept, value)
  7. setDefault(fitIntercept -> true)
  9. // 在训练模型前，是否对训练特征进行标准化。默认使用。
  10. // 模型的相关系数总是会返回原来的空间（不是标准化后的标准空间），所以这个过程对用户透明
  11. def setStandardization(value: Boolean): this.type = set(standardization, value)
  12. setDefault(standardization -> true)
  14. // ElasticNet混合参数
  15. // 当改值为0时，使用L2惩罚；当该值为1时，使用L1惩罚；当值在(0,1)之间时，使用L1惩罚和L2惩罚的组合
  16. def setElasticNetParam(value: Double): this.type = set(elasticNetParam, value)
  17. setDefault(elasticNetParam -> 0.0)
  19. // 最大迭代次数，默认是100
  20. def setMaxIter(value: Int): this.type = set(maxIter, value)
  21. setDefault(maxIter -> 100)
  23. // 收敛阈值
  24. def setTol(value: Double): this.type = set(tol, value)
  25. setDefault(tol -> 1E-6)
  27. // 样本权重列的列名。默认不设置。当不设置时，样本权重为1
  28. def setWeightCol(value: String): this.type = set(weightCol, value)
  30. // 最优化求解方法。实际有l-bfgs和带权最小二乘两种求解方法。
  31. // 当特征列数量超过4096时，默认使用l-bfgs求解，否则使用带权最小二乘求解。
  32. def setSolver(value: String): this.type = {
  33.     require(Set("auto", "l-bfgs", "normal").contains(value),
  34.       s"Solver $value was not supported. Supported options: auto, l-bfgs, normal")
  35.     set(solver, value)
  36.   }
  37. setDefault(solver -> "auto")
  39. // 设置treeAggregate的深度。默认情况下深度为2
  40. // 当特征维度较大或者分区较多时，可以调大该深度
  41. def setAggregationDepth(value: Int): this.type = set(aggregationDepth, value)
  42. setDefault(aggregationDepth -> 2)

2.2.2 训练模型

  train方法训练模型并返回LinearRegressionModel。方法的开始是处理数据集，生成需要的RDD。

  1. // Extract the number of features before deciding optimization solver.
  2. val numFeatures = dataset.select(col($(featuresCol))).first().getAs[Vector](0).size
  3. val w = if (!isDefined(weightCol) || $(weightCol).isEmpty) lit(1.0) else col($(weightCol))
  5. val instances: RDD[Instance] = dataset.select(
  6.     col($(labelCol)), w, col($(featuresCol))).rdd.map {
  7.     case Row(label: Double, weight: Double, features: Vector) =>
  8.         Instance(label, weight, features)  // 标签，权重，特征向量
  9. }
2.2.2.1 带权最小二乘

  当样本的特征维度小于4096并且solver为auto或者solver为normal时，用WeightedLeastSquares求解，这是因为WeightedLeastSquares只需要处理一次数据，
求解效率更高。WeightedLeastSquares的介绍见带权最小二乘。

  1. if (($(solver) == "auto" &&
  2.     numFeatures <= WeightedLeastSquares.MAX_NUM_FEATURES) || $(solver) == "normal") {
  4.     val optimizer = new WeightedLeastSquares($(fitIntercept), $(regParam),
  5.         elasticNetParam = $(elasticNetParam), $(standardization), true,
  6.         solverType = WeightedLeastSquares.Auto, maxIter = $(maxIter), tol = $(tol))
  7.     val model = optimizer.fit(instances)
  8.     // When it is trained by WeightedLeastSquares, training summary does not
  9.     // attach returned model.
  10.     val lrModel = copyValues(new LinearRegressionModel(uid, model.coefficients, model.intercept))
  11.     val (summaryModel, predictionColName) = lrModel.findSummaryModelAndPredictionCol()
  12.     val trainingSummary = new LinearRegressionTrainingSummary(
  13.         summaryModel.transform(dataset),
  14.         predictionColName,
  15.         $(labelCol),
  16.         $(featuresCol),
  17.         summaryModel,
  18.         model.diagInvAtWA.toArray,
  19.         model.objectiveHistory)
  21.     return lrModel.setSummary(Some(trainingSummary))
  22. }
2.2.2.2 拟牛顿法
  • 1 统计样本指标

  当样本的特征维度大于4096并且solver为auto或者solver为l-bfgs时，使用拟牛顿法求解最优解。使用拟牛顿法求解之前我们
需要先统计特征和标签的相关信息。

  1. val (featuresSummarizer, ySummarizer) = {
  2.       val seqOp = (c: (MultivariateOnlineSummarizer, MultivariateOnlineSummarizer),
  3.         instance: Instance) =>
  4.           (c._1.add(instance.features, instance.weight),
  5.             c._2.add(Vectors.dense(instance.label), instance.weight))
  7.       val combOp = (c1: (MultivariateOnlineSummarizer, MultivariateOnlineSummarizer),
  8.         c2: (MultivariateOnlineSummarizer, MultivariateOnlineSummarizer)) =>
  9.           (c1._1.merge(c2._1), c1._2.merge(c2._2))
  11.       instances.treeAggregate(
  12.         new MultivariateOnlineSummarizer, new MultivariateOnlineSummarizer
  13.       )(seqOp, combOp, $(aggregationDepth))
  14. }

  这里MultivariateOnlineSummarizer继承自MultivariateStatisticalSummary，它使用在线（online）的方式统计样本的均值、方差、最小值、最大值等指标。
具体的实现见MultivariateOnlineSummarizer。统计好指标之后，根据指标的不同选择不同的处理方式。

   如果标签的方差为0，并且不管我们是否选择使用偏置，系数均为0，此时并不需要训练模型。

  1.  val coefficients = Vectors.sparse(numFeatures, Seq())  // 系数为空
  2.  val intercept = yMean
  3.  val model = copyValues(new LinearRegressionModel(uid, coefficients, intercept))

  获取标签方差，特征均值、特征方差以及正则化项。

  1.  // if y is constant (rawYStd is zero), then y cannot be scaled. In this case
  2.  // setting yStd=abs(yMean) ensures that y is not scaled anymore in l-bfgs algorithm.
  3.  val yStd = if (rawYStd > 0) rawYStd else math.abs(yMean)
  4.  val featuresMean = featuresSummarizer.mean.toArray
  5.  val featuresStd = featuresSummarizer.variance.toArray.map(math.sqrt)
  6.  val bcFeaturesMean = instances.context.broadcast(featuresMean)
  7.  val bcFeaturesStd = instances.context.broadcast(featuresStd)
  9.  val effectiveRegParam = $(regParam) / yStd
  10.  val effectiveL1RegParam = $(elasticNetParam) * effectiveRegParam
  11.  val effectiveL2RegParam = (1.0 - $(elasticNetParam)) * effectiveRegParam
  • 2 定义损失函数
  1. val costFun = new LeastSquaresCostFun(instances, yStd, yMean, $(fitIntercept),
  2.       $(standardization), bcFeaturesStd, bcFeaturesMean, effectiveL2RegParam, $(aggregationDepth))

  损失函数LeastSquaresCostFun继承自DiffFunction[T]，用于表示最小二乘损失。它返回一个点L2正则化后的损失和梯度。
它使用方法def calculate(coefficients: BDV[Double]): (Double, BDV[Double])计算损失和梯度。这里coefficients表示一个特定的点。

  1. override def calculate(coefficients: BDV[Double]): (Double, BDV[Double]) = {
  2.     val coeffs = Vectors.fromBreeze(coefficients)
  3.     val bcCoeffs = instances.context.broadcast(coeffs)
  4.     val localFeaturesStd = bcFeaturesStd.value
  6.     val leastSquaresAggregator = {
  7.       val seqOp = (c: LeastSquaresAggregator, instance: Instance) => c.add(instance)
  8.       val combOp = (c1: LeastSquaresAggregator, c2: LeastSquaresAggregator) => c1.merge(c2)
  10.       instances.treeAggregate(
  11.         new LeastSquaresAggregator(bcCoeffs, labelStd, labelMean, fitIntercept, bcFeaturesStd,
  12.           bcFeaturesMean))(seqOp, combOp, aggregationDepth)
  13.     }
  15.     val totalGradientArray = leastSquaresAggregator.gradient.toArray //梯度
  16.     bcCoeffs.destroy(blocking = false)
  18.     val regVal = if (effectiveL2regParam == 0.0) {
  19.       0.0
  20.     } else {
  21.       var sum = 0.0
  22.       coeffs.foreachActive { (index, value) =>
  23.         // 下面的代码计算正则化项的损失和梯度，并将梯度添加到totalGradientArray中
  24.         sum += {
  25.           if (standardization) {
  26.             totalGradientArray(index) += effectiveL2regParam * value
  27.             value * value
  28.           } else {
  29.             if (localFeaturesStd(index) != 0.0) {
  30.               // 如果`standardization`为false，我们仍然标准化数据加快收敛速度。获得的结果，我们需要执行反标准化
  31.               // ，来得到正确的目标函数
  32.               val temp = value / (localFeaturesStd(index) * localFeaturesStd(index))
  33.               totalGradientArray(index) += effectiveL2regParam * temp
  34.               value * temp
  35.             } else {
  36.               0.0
  37.             }
  38.           }
  39.         }
  40.       }
  41.       0.5 * effectiveL2regParam * sum
  42.     }
  44.     (leastSquaresAggregator.loss + regVal, new BDV(totalGradientArray))
  45.   }

  这里LeastSquaresAggregator用来计算最小二乘损失函数的梯度和损失。为了在优化过程中提高收敛速度，防止大方差
的特征在训练时产生过大的影响，将特征缩放到单元方差并且减去均值，可以减少条件数。当使用截距进行训练时，处在缩放后空间的目标函数
如下：


$$
\begin{align}
L &= 1/2N ||\sum_i w_i(x_i - \bar{x_i}) / \hat{x_i} - (y - \bar{y}) / \hat{y}||^2
\end{align}
$$

  在这个公式中，$\bar{x_i}$是$x_i$的均值，$\hat{x_i}$是$x_i$的标准差，$\bar{y}$是标签的均值，$\hat{y}$ 是标签的标准差。

  如果不使用截距，我们可以使用同样的公式。不同的是$\bar{y}$和$\bar{x_i}$分别用0代替。这个公式可以重写为如下的形式。


$$
\begin{align}
L &= 1/2N ||\sum_i (w_i/\hat{x_i})x_i - \sum_i (w_i/\hat{x_i})\bar{x_i} - y / \hat{y} + \bar{y} / \hat{y}||^2 \
&= 1/2N ||\sum_i w_i^\prime x_i - y / \hat{y} + offset||^2 = 1/2N diff^2
\end{align}
$$

  在这个公式中，$w_i^\prime$是有效的相关系数，通过$w_i/\hat{x_i}$计算。offset是$- \sum_i (w_i/\hat{x_i})\bar{x_i} + \bar{y} / \hat{y}$，
而diff是$\sum_i w_i^\prime x_i - y / \hat{y} + offset$。

  注意，相关系数和offset不依赖于训练数据集，所以它们可以提前计算。

  现在，目标函数的一阶导数如下所示：


$$
\begin{align}
\frac{\partial L}{\partial w_i} &= diff/N (x_i - \bar{x_i}) / \hat{x_i}
\end{align}
$$

  然而，$(x_i - \bar{x_i})$是一个密集的计算，当训练数据集是稀疏的格式时，这不是一个理想的公式。通过添加一个稠密项 $\bar{x_i} / \hat{x_i}$到
公式的末尾可以解决这个问题。目标函数的一阶导数如下所示：


$$
\begin{align}
\frac{\partial L}{\partial wi} &=1/N \sum_j diff_j (x{ij} - \bar{xi}) / \hat{x_i} \
&= 1/N ((\sum_j diff_j x{ij} / \hat{xi}) - diffSum \bar{x_i} / \hat{x_i}) \
&= 1/N ((\sum_j diff_j x{ij} / \hat{x_i}) + correction_i)
\end{align}
$$

  这里，$correction_i = - diffSum \bar{x_i} / \hat{x_i}$。通过一个简单的数学推导，我们就可以知道diffSum实际上为0。


$$
\begin{align}
diffSum &= \sumj (\sum_i w_i(x{ij} - \bar{x_i})
/ \hat{x_i} - (y_j - \bar{y}) / \hat{y}) \
&= N * (\sum_i w_i(\bar{x_i} - \bar{x_i}) / \hat{x_i} - (\bar{y} - \bar{y}) / \hat{y}) \
&= 0
\end{align}
$$

  所以，目标函数的一阶导数仅仅依赖于训练数据集，我们可以简单的通过分布式的方式来计算，并且对稀疏格式也很友好。


$$
\begin{align}
\frac{\partial L}{\partial wi} &= 1/N ((\sum_j diff_j x{ij} / \hat{x_i})
\end{align}
$$

  我们首先看有效系数$w_i/\hat{x_i}$和offset的实现。

  1. @transient private lazy val effectiveCoefAndOffset = {
  2.     val coefficientsArray = bcCoefficients.value.toArray.clone() //系数，表示公式中的w
  3.     val featuresMean = bcFeaturesMean.value
  4.     var sum = 0.0
  5.     var i = 0
  6.     val len = coefficientsArray.length
  7.     while (i < len) {
  8.       if (featuresStd(i) != 0.0) {
  9.         coefficientsArray(i) /=  featuresStd(i)
  10.         sum += coefficientsArray(i) * featuresMean(i)
  11.       } else {
  12.         coefficientsArray(i) = 0.0
  13.       }
  14.       i += 1
  15.     }
  16.     val offset = if (fitIntercept) labelMean / labelStd - sum else 0.0
  17.     (Vectors.dense(coefficientsArray), offset)
  18.   }

  我们再来看看add方法和merge方法的实现。当添加一个样本后，需要更新相应的损失值和梯度值。

  1. def add(instance: Instance): this.type = {
  2.   instance match { case Instance(label, weight, features) =>
  3.   if (weight == 0.0) return this
  4.   // 计算diff
  5.   val diff = dot(features, effectiveCoefficientsVector) - label / labelStd + offset
  6.   if (diff != 0) {
  7.       val localGradientSumArray = gradientSumArray
  8.       val localFeaturesStd = featuresStd
  9.       features.foreachActive { (index, value) =>
  10.          if (localFeaturesStd(index) != 0.0 && value != 0.0) {
  11.            localGradientSumArray(index) += weight * diff * value / localFeaturesStd(index) // 见公式(11)
  12.          }
  13.       }
  14.       lossSum += weight * diff * diff / 2.0   //见公式(3)
  15.   }
  16.   totalCnt += 1
  17.   weightSum += weight
  18.   this
  19. }
  21. def merge(other: LeastSquaresAggregator): this.type = {
  22.     if (other.weightSum != 0) {
  23.       totalCnt += other.totalCnt
  24.       weightSum += other.weightSum
  25.       lossSum += other.lossSum
  27.       var i = 0
  28.       val localThisGradientSumArray = this.gradientSumArray
  29.       val localOtherGradientSumArray = other.gradientSumArray
  30.       while (i < dim) {
  31.         localThisGradientSumArray(i) += localOtherGradientSumArray(i)
  32.         i += 1
  33.       }
  34.     }
  35.     this
  36.   }

  最后，根据下面的公式分别获取损失和梯度。

  1.   def loss: Double = {
  2.     lossSum / weightSum
  3.   }
  5.   def gradient: Vector = {
  6.     val result = Vectors.dense(gradientSumArray.clone())
  7.     scal(1.0 / weightSum, result)
  8.     result
  9.   }
  • 3 选择最优化方法
  1.     val optimizer = if ($(elasticNetParam) == 0.0 || effectiveRegParam == 0.0) {
  2.       new BreezeLBFGS[BDV[Double]]($(maxIter), 10, $(tol))
  3.     } else {
  4.       val standardizationParam = $(standardization)
  5.       def effectiveL1RegFun = (index: Int) => {
  6.         if (standardizationParam) {
  7.           effectiveL1RegParam
  8.         } else {
  9.           // If `standardization` is false, we still standardize the data
  10.           // to improve the rate of convergence; as a result, we have to
  11.           // perform this reverse standardization by penalizing each component
  12.           // differently to get effectively the same objective function when
  13.           // the training dataset is not standardized.
  14.           if (featuresStd(index) != 0.0) effectiveL1RegParam / featuresStd(index) else 0.0
  15.         }
  16.       }
  17.       new BreezeOWLQN[Int, BDV[Double]]($(maxIter), 10, effectiveL1RegFun, $(tol))
  18.     }

  如果没有正则化项或者只有L2正则化项，使用BreezeLBFGS来处理最优化问题，否则使用BreezeOWLQN。BreezeLBFGS和BreezeOWLQN
的原理在相关章节会做具体介绍。

  • 4 获取结果，并做相应转换
  1. val initialCoefficients = Vectors.zeros(numFeatures)
  2.     val states = optimizer.iterations(new CachedDiffFunction(costFun),
  3.       initialCoefficients.asBreeze.toDenseVector)
  5.     val (coefficients, objectiveHistory) = {
  6.       val arrayBuilder = mutable.ArrayBuilder.make[Double]
  7.       var state: optimizer.State = null
  8.       while (states.hasNext) {
  9.         state = states.next()
  10.         arrayBuilder += state.adjustedValue
  11.       }
  13.       // 从标准空间转换到原来的空间
  14.       val rawCoefficients = state.x.toArray.clone()
  15.       var i = 0
  16.       val len = rawCoefficients.length
  17.       while (i < len) {
  18.         rawCoefficients(i) *= { if (featuresStd(i) != 0.0) yStd / featuresStd(i) else 0.0 }
  19.         i += 1
  20.       }
  22.       (Vectors.dense(rawCoefficients).compressed, arrayBuilder.result())
  23.     }
  25.     // 系数收敛之后，intercept的计算可以通过封闭(`closed form`)的形式计算出来，详细的讨论如下：
  26.     // http://stats.stackexchange.com/questions/13617/how-is-the-intercept-computed-in-glmnet
  27.     val intercept = if ($(fitIntercept)) {
  28.       yMean - dot(coefficients, Vectors.dense(featuresMean))
  29.     } else {
  30.       0.0
  31.     }
免责声明： 以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。
@小牛知识库 xnip.cn