登录
目录
当前位置： 首页 > 文档资料 > Spark 机器学习算法研究和源码分析 >

最优化算法 - NNLS(非负最小二乘)

优质
小牛编辑
135浏览
2023-12-01

  spark中的非负正则化最小二乘法并不是wiki中介绍的NNLS的实现，而是做了相应的优化。它使用改进投影梯度法结合共轭梯度法来求解非负最小二乘。
在介绍spark的源码之前，我们要先了解什么是最小二乘法以及共轭梯度法。

1 最小二乘法

1.1 最小二乘问题

  在某些最优化问题中，目标函数由若干个函数的平方和构成，它的一般形式如下所示：

1.1

  其中x=（x1,x2,…,xn），一般假设m>=n。把极小化这类函数的问题称为最小二乘问题。

1.2

  当$f{i}(x)$为x的线性函数时，称（1.2）为线性最小二乘问题，当$f{i}(x)$为x的非线性函数时，称（1.2）为非线性最小二乘问题。

1.2 线性最小二乘问题

  在公式（1.1）中，假设

1.3

  其中，p是n维列向量，bi是实数，这样我们可以用矩阵的形式表示（1.1）式。令

1.3

  A是m * n矩阵，b是m维列向量。则

1.4

  因为F(x)是凸的，所以对（1.4）求导可以得到全局极小值，令其导数为0，我们可以得到这个极小值。

1.5

  假设A为满秩，$A^{T}A$为n阶对称正定矩阵，我们可以求得x的值为以下的形式：

1.6

1.3 非线性最小二乘问题

  假设在（1.1）中，$f{i}(x)$为非线性函数，且F(x)有连续偏导数。由于$f{i}(x)$为非线性函数，所以（1.2）中的非线性最小二乘无法套用（1.6）中的公式求得。
解这类问题的基本思想是，通过解一系列线性最小二乘问题求非线性最小二乘问题的解。设$x^{(k)}$是解的第k次近似。在$x^{(k)}$时，将函数$f_{i}(x)$线性化，从而将非线性最小二乘转换为线性最小二乘问题，
用（1.6）中的公式求解极小点$x^{(k+1)}$ ，把它作为非线性最小二乘问题解的第k+1次近似。然后再从$x^{(k+1)}$出发，继续迭代。下面将来推导迭代公式。令

1.7

  上式右端是$f_{i}(x)$在$x^{(k)}$处展开的一阶泰勒级数多项式。令

1.8

  用∅(x)近似F(x)，从而用∅(x)的极小点作为目标函数F(x)的极小点的估计。现在求解线性最小二乘问题

1.9

  把（1.9）写成

1.10

  在公式（1.10）中，

1.10

  将$A_{k}$和b带入公式（1.5）中，可以得到，

1.11

  如果$A{k}$为列满秩，且$A{k}^{T}A_{k}$是对称正定矩阵，那么由（1.11）可以得到x的极小值。

1.12

  可以推导出$2A{k}^{T}f{k}$是目标函数F(x)在$x^{(k)}$处的梯度，$2A{k}^{T}A{k}$是函数∅(x)的海森矩阵。所以（1.12）又可以写为如下形式。

1.13

  公式（1.13）称为Gauss-Newton公式。向量

1.14

  称为点$x^{(k)}$处的Gauss-Newton方向。为保证每次迭代能使目标函数值下降（至少不能上升），在求出$d^{(k)}$后，不直接使用$x^{(k)}+d^{(k)}$作为k+1次近似，而是从$x^{(k)}$出发，沿$d^{(k)}$方向进行一维搜索。

1.15

  求出步长$\lambda ^{(k)}$后，令

1.16

  最小二乘的计算步骤如下:

  • （1） 给定初始点$x^{(1)}$，允许误差ε>0，k=1

  • （2） 计算函数值$f{i}(x)$，得到向量$f^{(k)}$，再计算一阶偏导，得到m*n矩阵$A{(k)}$

  • （3） 解方程组（1.14）求得Gauss-Newton方向$d^{(k)}$

  • （4）从$x^{(k)}$出发，沿着$d^{(k)}$作一维搜索，求出步长$\lambda ^{(k)}$ ，并令$x^{(k+1)}=x^{(k)}-\lambda d^{(k)}$

  • （5）若$||x^{(k+1)}-x^{(k)}||<=\epsilon$停止迭代，求出x，否则，k=k+1，返回步骤（2）

  在某些情况下，矩阵$A^{T}A$是奇异的，这种情况下，我们无法求出它的逆矩阵，因此我们需要对其进行修改。用到的基本技巧是将一个正定对角矩阵添加到$A^{T}A$上，改变原来矩阵的特征值结构，使其变成条件较好的对称正定矩阵。
典型的算法是Marquardt。

1.17

  其中，I是n阶单位矩阵，alpha是一个正实数。当alpha为0时，$d^{(k)}$就是Gauss-Newton方向，当alpha充分大时，这时$d^{(k)}$接近F(x)在$x^{(k)}$处的最速下降方向。算法的具体过程见参考文献【1】。

2 共轭梯度法

2.1 共轭方向

  在讲解共轭梯度法之前，我们需要先知道什么是共轭方向，下面的定义给出了答案。

  定义2.1 设A是n*n对称正定矩阵，若两个方向$d^{(1)}$ 和$d^{(2)}$满足

2.1

则称这两个方向关于A共轭。若$d^{(1)},d^{(2)},…,d^{(k)}$是k个方向，它们两两关于A共轭，则称这组方向是关于A共轭的。即

2.2

在上述定义中，如果A是单位矩阵，那么两个方向关于A共轭等价于两个方向正交。如果A是一般的对称正定矩阵，$d^{(i)}$与$d^{(j)}$共轭，就是$d^{(i)}$与$Ad^{(j)}$正交。共轭方向有一些重要的性质。

  定理2.1 设A是n阶对称正定矩阵，$d^{(1)},d^{(2)},…,d^{(k)}$是k个A的共轭的非零向量，则这个向量组线性无关。

  定理2.2 (扩张子空间定理） 设有函数

2.2.a1

  其中，A是n阶对称正定矩阵，$d^{(1)},d^{(2)},…,d^{(k)}$是k个A的共轭的非零向量，以任意的$x^{(1)}$为初始点，
沿$d^{(1)},d^{(2)},…,d^{(k)}$进行一维搜索，得到$x^{(2)},x^{(3)},…,x^{(k+1)}$，则$d^{(k+1)}$是线性流型
$x^{(1)}+H_{k}$上的唯一极小点，特别的，当k=n时，$x^{(n+1)}$是函数f(x)的唯一极小点。其中，

2.2.a2

是$d^{(1)},d^{(2)},…,d^{(k)}$生成的子空间。

  这两个定理在文献【1】中有详细证明。

2.2 共轭梯度法

  共轭梯度法的基本思想是把共轭性与最速下降方法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。这里我们仅仅讨论二次凸函数的共轭梯度法。

  考虑问题

2.3

  其中A是对称正定矩阵，c是常数。

  具体求解方式如下：

  首先给定任何一个初始点$x^{(1)}$ ，计算目标函数f(x)在这点的梯度$g{(1)}$ ，若$||g{(1)}||=0$ ，则停止计算；否则令

2.4

  沿方向$d^{(1)}$搜索，得到点$x^{(2)}$ 。计算$x^{(2)}$处的梯度，若$||g{(2)}||!=0$，则利用$g{(2)}$和$d^{(1)}$构造第二个搜索方向$d^{(2)}$，再沿$d^{(2)}$搜索。

  一般的，若已知$x^{(k)}$和搜索方向$d^{(k)}$，则从$x^{(k))}$出发，沿方向$d^{(k)}$搜索，得到

2.5

  其中步长lambda满足

2.5.a1

  此时可以求得lambda的显式表达。令

2.5.a2

  通过求导可以求上面公式的极小值，即

2.6

  根据二次函数梯度表达式，（2.6）式可以推出如下方程

2.7

  由（2.7）式可以得到

2.8

  计算f(x)在$x^{(k+1)}$处的梯度，若$||g{k+1}||=0$ ，则停止计算，
否则用$g{(k+1)}$和$d^{(k)}$构造下一个搜索方向$d^{(k+1)}$ ，并使$d^{(k)}$与$d^{(k+1)}$共轭。按照这种设想，令

2.9

  在公式（2.9）两端同时乘以$d^{(k)T}A$，并令

2.10

  可以求得

2.11

  再从$x^{(k+1)}$出发，沿$d^{(k+1)}$方向搜索。综上分析 ，在第1个搜索方向取负梯度的前提下，重复使用公式（2.5）、（2.8）、（2.9）、（2.11），我们就能够构造一组搜索方向。当然，前提是这组方向是关于A共轭的。
定理2.3说明了这组方向是共轭的。

  定理2.3 对于正定二次函数（2.3），具有精确一维搜索的的共轭梯度法在m<=n次一维搜索后终止，并且对于所有i(1<=i<=m)，下列关系成立：

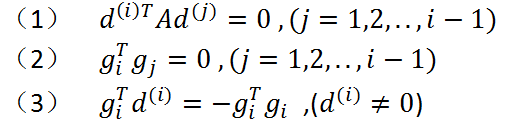
2.11.a1

  还可以证明，对于正定二次函数，运用共轭梯度法时，不做矩阵运算也可以计算变量beta_k。

  定理2.4 对于正定二次函数，共轭梯度法中因子beta_k具有下列表达式

2.12

  对于二次凸函数，共轭梯度法的计算步骤如下：

NNLS.2.1

3 最小二乘法在spark中的具体实现

  Spark ml中解决最小二乘可以选择两种方式，一种是非负正则化最小二乘，一种是乔里斯基分解（Cholesky）。

  乔里斯基分解分解是把一个对称正定的矩阵表示成一个上三角矩阵U的转置和其本身的乘积的分解。在ml代码中，直接调用netlib-java封装的dppsv方法实现。

  1. lapack.dppsv(“u”, k, 1, ne.ata, ne.atb, k, info)

  可以深入dppsv代码（Fortran代码）了解更深的细节。我们分析的重点是非负正则化最小二乘的实现，因为在某些情况下，方程组的解为负数是没有意义的。虽然方程组可以得到精确解，但却不能取负值解。在这种情况下，其非负最小二乘解比方程的精确解更有意义。非负最小二乘问题要求解的问题如下公式

3.1

其中ata是半正定矩阵。

  在ml代码中，org.apache.spark.mllib.optimization.NNLS对象实现了非负最小二乘算法。该算法结合了投影梯度算法和共轭梯度算法来求解。

  首先介绍NNLS对象中的Workspace类。

  1. class Workspace(val n: Int) {
  2.   val scratch = new Array[Double](n)
  3.   val grad = new Array[Double](n)  //投影梯度
  4.   val x = new Array[Double](n)
  5.   val dir = new Array[Double](n)   //搜索方向
  6.   val lastDir = new Array[Double](n)
  7.   val res = new Array[Double](n)  //梯度
  8. }

  在Workspace中，res表示梯度，grad表示梯度的投影，dir表示迭代过程中的搜索方向（共轭梯度中的搜索方向$d^{(k)}$），scratch代表公式（2.8）中的
$d^{(k)T}A$。

  NNLS对象中，sort方法用来解最小二乘，它通过迭代求解极小值。我们将分步骤剖析该方法。

  • （1）确定迭代次数。
  1. val iterMax = math.max(400, 20 * n)
  • （2）求梯度。

  在每次迭代内部，第一步会求梯度res，代码如下

  1. //y := alpha*A*x + beta*y 即  y:=1.0 * ata * x + 0.0 * res
  2. blas.dgemv("N", n, n, 1.0, ata, n, x, 1, 0.0, res, 1)
  3. // ata*x - atb
  4. blas.daxpy(n, -1.0, atb, 1, res, 1)

  dgemv方法的作用是得到y := alpha*A*x + beta*y，在本代码中表示res=ata*x。daxpy方法的作用是得到y:=step*x +y,在本代码中表示res=ata*x-atb，即梯度。

  • （3）求梯度的投影矩阵

  求梯度矩阵的投影矩阵的依据如下公式。

3.2

  详细代码如下所示：

  1. //转换为投影矩阵
  2. i = 0
  3. while (i < n) {
  4.    if (grad(i) > 0.0 && x(i) == 0.0) {
  5.      grad(i) = 0.0
  6.    }
  7.    i = i + 1
  8. }
  • （4）求搜索方向。

  在第一次迭代中，搜索方向即为梯度方向。如下面代码所示。

  1. //在第一次迭代中，搜索方向dir即为梯度方向
  2. blas.dcopy(n, grad, 1, dir, 1)

  在第k次迭代中，搜索方向由梯度方向和前一步的搜索方向共同确定，计算依赖的公式是（2.9）。具体代码有两行

  1. val alpha = ngrad / lastNorm
  2. //alpha*lastDir + dir，此时dir为梯度方向 
  3. blas.daxpy(n, alpha, lastDir, 1, dir, 1)

  此处的alpha就是根据公式（2.12）计算的。

  • （5）计算步长。

  知道了搜索方向，我们就可以依据公式（2.8）来计算步长。

  1. def steplen(dir: Array[Double], res: Array[Double]): Double = {
  2.   //top = g * d
  3. val top = blas.ddot(n, dir, 1, res, 1)
  4.   // y := alpha*A*x + beta*y.
  5.   // scratch = d * ata
  6. blas.dgemv("N", n, n, 1.0, ata, n, dir, 1, 0.0, scratch, 1)
  7.   //公式（2.8），添加1e-20是为了避免分母为0
  8. //g*d/d*ata*d
  9.   top / (blas.ddot(n, scratch, 1, dir, 1) + 1e-20)
  10. }
  • （6）调整步长并修改迭代值。

  因为解是非负的，所以步长需要做一定的处理，如果步长与搜索方向的乘积大于x的值，那么重置步长。重置逻辑如下：

  1. i = 0
  2. while (i < n) {
  3.    if (step * dir(i) > x(i)) {
  4.      //如果步长过大，那么二者的商替代
  5.      step = x(i) / dir(i)
  6.    }
  7.    i = i + 1
  8. }

  最后，修改x的值，完成该次迭代。

  1. i = 0
  2. while (i < n) {
  3. // x(i)趋向为0
  4.   if (step * dir(i) > x(i) * (1 - 1e-14)) {
  5.     x(i) = 0
  6.     lastWall = iterno
  7.   } else {
  8.     x(i) -= step * dir(i)
  9.   }
  10.   i = i + 1
  11. }

4 参考文献

【1】陈宝林，最优化理论和算法

【2】Boris T. Polyak，The conjugate gradient method in extreme problems

【3】https://en.wikipedia.org/wiki/Non-negative_least_squares

免责声明： 以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。
@小牛知识库 xnip.cn