用python获取线性回归中的不确定性值
我有一些数据比如
arr = [
[30.0, 0.0257],
[30.0, 0.0261],
[30.0, 0.0261],
[30.0, 0.026],
[30.0, 0.026],
[35.0, 0.0387],
[35.0, 0.0388],
[35.0, 0.0387],
[35.0, 0.0388],
[35.0, 0.0388],
[40.0, 0.0502],
[40.0, 0.0503],
[40.0, 0.0502],
[40.0, 0.0498],
[40.0, 0.0502],
[45.0, 0.0582],
[45.0, 0.0574],
[45.0, 0.058],
[45.0, 0.058],
[45.0, 0.058],
[50.0, 0.0702],
[50.0, 0.0702],
[50.0, 0.0698],
[50.0, 0.0704],
[50.0, 0.0703],
[55.0, 0.0796],
[55.0, 0.0808],
[55.0, 0.0803],
[55.0, 0.0805],
[55.0, 0.0806],
]
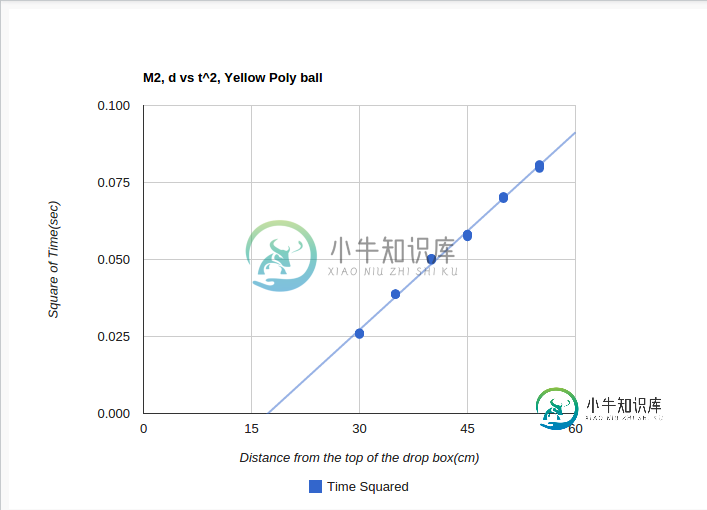
在谷歌图表API中
我正试图对此进行线性回归,即试图找到趋势线的斜率和(y-)截距,以及斜率中的不确定性和截距中的不确定性。
当我画趋势线时,谷歌图表应用编程接口已经找到了斜率和截距值,但是我不确定如何找到不确定性。
我一直在使用Excel中的LINEST函数来执行此操作,但我发现这非常麻烦,因为我的所有数据都在Python中。
所以我的问题是,如何使用Python找到LINEST中得到的两个不确定性值?
我很抱歉问了这样一个基本的问题。
我在Python和Javascript方面很在行,但我在回归分析方面很差,所以当我试图在文档中查找它们时,由于术语比较难,我感到非常困惑。
我希望使用一些著名的Python库,不过如果我能在googlechartsapi中实现这一点,那将是非常理想的。
共有1个答案
可以使用如下statsmodels完成:
import statsmodels.api as sm
import numpy as np
y=[];x=[]
for item in arr:
x.append(item[0])
y.append(item[1])
# include constant in ols models, which is not done by default
x = sm.add_constant(x)
model = sm.OLS(y,x)
results = model.fit()
然后,您可以按以下方式访问所需的值。截距和斜率由以下给出:
results.params # linear coefficients
# array([-0.036924 , 0.0021368])
我想你指的是标准错误,当你提到不确定性时,它们可以这样访问:
results.bse # standard errors of the parameter estimates
# array([ 1.03372221e-03, 2.38463106e-05])
可以通过运行
>>> print results.summary()
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.997
Model: OLS Adj. R-squared: 0.996
Method: Least Squares F-statistic: 8029.
Date: Fri, 26 Sep 2014 Prob (F-statistic): 5.61e-36
Time: 05:47:08 Log-Likelihood: 162.43
No. Observations: 30 AIC: -320.9
Df Residuals: 28 BIC: -318.0
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const -0.0369 0.001 -35.719 0.000 -0.039 -0.035
x1 0.0021 2.38e-05 89.607 0.000 0.002 0.002
==============================================================================
Omnibus: 7.378 Durbin-Watson: 0.569
Prob(Omnibus): 0.025 Jarque-Bera (JB): 2.079
Skew: 0.048 Prob(JB): 0.354
Kurtosis: 1.714 Cond. No. 220.
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
这也可能有助于总结结果模型的属性。
我没有与Excel中的LINEST进行比较。我也不知道这是否可能只使用谷歌图表应用编程接口。
-
我正在运行我在buitin网站上看到的一个关于张量流线性回归的代码,它总是给我一个错误,我不知道代码有什么问题。首先我以为这是我的ide,然后当我切换到jupyter实验室时,它显示了我在这一点上的错误 首先我以为这是我的ide,然后当我切换到jupyter实验室时,它显示了我在这一点上的错误
-
线性回归是最简单的回归方法,它的目标是使用超平面拟合数据集,即学习一个线性模型以尽可能准确的预测实值输出标记。 单变量模型 模型 $$f(x)=w^Tx+b$$ 在线性回归问题中,一般使用最小二乘参数估计($$L_2$$损失),定义目标函数为 $$J={\arg min}{(w,b)}\sum{i=1}^{m}(y_i-wx_i-b)^2$$ 均方误差(MSE) $$MSE = \frac{1}{
-
线性回归输出是一个连续值,因此适用于回归问题。回归问题在实际中很常见,如预测房屋价格、气温、销售额等连续值的问题。与回归问题不同,分类问题中模型的最终输出是一个离散值。我们所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适用于分类问题。 由于线性回归和softmax回归都是单层神经网络,它们涉及的概念和技术同样适用于大多数的深度学习模型。我们首先
-
本例仅使用糖尿病数据集的第一个特征,来展示线性回归在二维空间上的表现。下图中的直线, 即是线性回归所确定的一个界限,其目标是使得数据集中的实际值与线性回归所得的预测值之间的残差平方和最小。 同时也计算了回归系数、残差平方和以及解释方差得分,来判断该线性回归模型的质量。 原文解释和代码不符合: 实际上计算了回归系数, 均方误差(MSE),判定系数(r2_score) 判定系数和解释方差得分并不绝对相
-
回归问题的条件或者说前提是 1) 收集的数据 2) 假设的模型,即一个函数,这个函数里含有未知的参数,通过学习,可以估计出参数。然后利用这个模型去预测/分类新的数据。 1 线性回归的概念 线性回归假设特征和结果都满足线性。即不大于一次方。收集的数据中,每一个分量,就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数,向量表示形式: 这个就是一个组合问题,
-
本文向大家介绍sklearn+python:线性回归案例,包括了sklearn+python:线性回归案例的使用技巧和注意事项,需要的朋友参考一下 使用一阶线性方程预测波士顿房价 载入的数据是随sklearn一起发布的,来自boston 1993年之前收集的506个房屋的数据和价格。load_boston()用于载入数据。 输出内容为: 可以看到测试集上准确率并不高,应该是欠拟合。 使用多项式做线

