python编程线性回归代码示例
用python进行线性回归分析非常方便,有现成的库可以使用比如:numpy.linalog.lstsq例子、scipy.stats.linregress例子、pandas.ols例子等。
不过本文使用sklearn库的linear_model.LinearRegression,支持任意维度,非常好用。
一、二维直线的例子
预备知识:线性方程y=a∗x+b。y=a∗x+b表示平面一直线
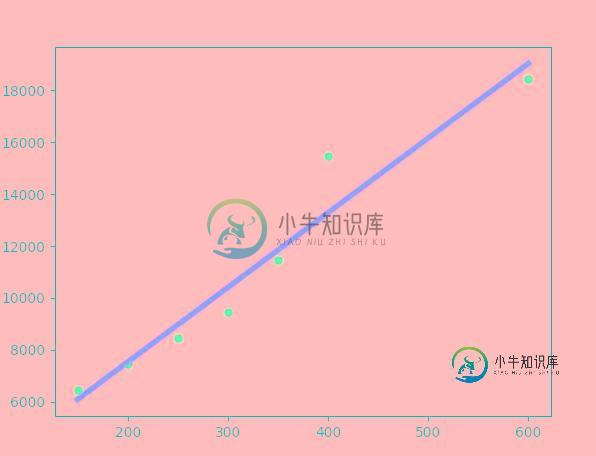
下面的例子中,我们根据房屋面积、房屋价格的历史数据,建立线性回归模型。
然后,根据给出的房屋面积,来预测房屋价格。这里是数据来源
import pandas as pd from io import StringIO from sklearn import linear_model import matplotlib.pyplot as plt # 房屋面积与价格历史数据(csv文件) csv_data = 'square_feet,price\n150,6450\n200,7450\n250,8450\n300,9450\n350,11450\n400,15450\n600,18450\n' # 读入dataframe df = pd.read_csv(StringIO(csv_data)) print(df) # 建立线性回归模型 regr = linear_model.LinearRegression() # 拟合 regr.fit(df['square_feet'].reshape(-1, 1), df['price']) # 注意此处.reshape(-1, 1),因为X是一维的! # 不难得到直线的斜率、截距 a, b = regr.coef_, regr.intercept_ # 给出待预测面积 area = 238.5 # 方式1:根据直线方程计算的价格 print(a * area + b) # 方式2:根据predict方法预测的价格 print(regr.predict(area)) # 画图 # 1.真实的点 plt.scatter(df['square_feet'], df['price'], color='blue') # 2.拟合的直线 plt.plot(df['square_feet'], regr.predict(df['square_feet'].reshape(-1,1)), color='red', linewidth=4) plt.show()
二、三维平面的例子
预备知识:线性方程z=a∗x+b∗y+c。z=a∗x+b∗y+c 表示空间一平面
由于找不到真实数据,只好自己虚拟一组数据。
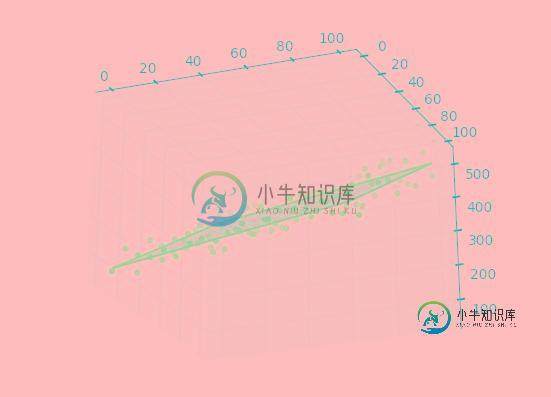
import numpy as np from sklearn import linear_model from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt xx, yy = np.meshgrid(np.linspace(0,10,10), np.linspace(0,100,10)) zz = 1.0 * xx + 3.5 * yy + np.random.randint(0,100,(10,10)) # 构建成特征、值的形式 X, Z = np.column_stack((xx.flatten(),yy.flatten())), zz.flatten() # 建立线性回归模型 regr = linear_model.LinearRegression() # 拟合 regr.fit(X, Z) # 不难得到平面的系数、截距 a, b = regr.coef_, regr.intercept_ # 给出待预测的一个特征 x = np.array([[5.8, 78.3]]) # 方式1:根据线性方程计算待预测的特征x对应的值z(注意:np.sum) print(np.sum(a * x) + b) # 方式2:根据predict方法预测的值z print(regr.predict(x)) # 画图 fig = plt.figure() ax = fig.gca(projection='3d') # 1.画出真实的点 ax.scatter(xx, yy, zz) # 2.画出拟合的平面 ax.plot_wireframe(xx, yy, regr.predict(X).reshape(10,10)) ax.plot_surface(xx, yy, regr.predict(X).reshape(10,10), alpha=0.3) plt.show()
效果图
总结
以上就是本文关于python编程线性回归代码示例的全部内容,希望对大家有所帮助。感兴趣的朋友可以继续参阅本站:
python八大排序算法速度实例对比
详解K-means算法在Python中的实现
Python算法之图的遍历
如有不足之处,欢迎留言指出。感谢朋友们对本站的支持!
-
本文向大家介绍Python scikit-learn 做线性回归的示例代码,包括了Python scikit-learn 做线性回归的示例代码的使用技巧和注意事项,需要的朋友参考一下 一、概述 机器学习算法在近几年大数据点燃的热火熏陶下已经变得被人所“熟知”,就算不懂得其中各算法理论,叫你喊上一两个著名算法的名字,你也能昂首挺胸脱口而出。当然了,算法之林虽大,但能者还是有限,能适应某些环境并取得较
-
本文向大家介绍sklearn+python:线性回归案例,包括了sklearn+python:线性回归案例的使用技巧和注意事项,需要的朋友参考一下 使用一阶线性方程预测波士顿房价 载入的数据是随sklearn一起发布的,来自boston 1993年之前收集的506个房屋的数据和价格。load_boston()用于载入数据。 输出内容为: 可以看到测试集上准确率并不高,应该是欠拟合。 使用多项式做线
-
本文向大家介绍Python编程实现使用线性回归预测数据,包括了Python编程实现使用线性回归预测数据的使用技巧和注意事项,需要的朋友参考一下 本文中,我们将进行大量的编程——但在这之前,我们先介绍一下我们今天要解决的实例问题。 1) 预测房子价格 房价大概是我们中国每一个普通老百姓比较关心的问题,最近几年保障啊,小编这点微末工资着实有点受不了。 我们想预测特定房子的价值,预测依据是房屋面积。 2
-
线性回归是最简单的回归方法,它的目标是使用超平面拟合数据集,即学习一个线性模型以尽可能准确的预测实值输出标记。 单变量模型 模型 $$f(x)=w^Tx+b$$ 在线性回归问题中,一般使用最小二乘参数估计($$L_2$$损失),定义目标函数为 $$J={\arg min}{(w,b)}\sum{i=1}^{m}(y_i-wx_i-b)^2$$ 均方误差(MSE) $$MSE = \frac{1}{
-
线性回归输出是一个连续值,因此适用于回归问题。回归问题在实际中很常见,如预测房屋价格、气温、销售额等连续值的问题。与回归问题不同,分类问题中模型的最终输出是一个离散值。我们所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适用于分类问题。 由于线性回归和softmax回归都是单层神经网络,它们涉及的概念和技术同样适用于大多数的深度学习模型。我们首先
-
本例仅使用糖尿病数据集的第一个特征,来展示线性回归在二维空间上的表现。下图中的直线, 即是线性回归所确定的一个界限,其目标是使得数据集中的实际值与线性回归所得的预测值之间的残差平方和最小。 同时也计算了回归系数、残差平方和以及解释方差得分,来判断该线性回归模型的质量。 原文解释和代码不符合: 实际上计算了回归系数, 均方误差(MSE),判定系数(r2_score) 判定系数和解释方差得分并不绝对相

