13.2 为前馈神经网络选择激励函数
简单起见,目前为止我们只讨论了多层前馈神经网络中用到的sigmoid激励函数,它应用到了第12章介绍的多层感知器的隐层和输出层中。我们把此激励函数称为sigmoid函数,因为这是学术文献中的常用叫法——更为准确的定义应该是逻辑斯谛函数(logistic function),或者负对数似然函数(negative log-likehood function)。在本节的后续内容中,读者将学到更多的sigmoid系列激励函数,它们常用于实现多层神经网络。
从技术上讲,任何一个函数只要是可微的,我们就可以将其用作多层神经网络的激励函数。在Adaline中,我们甚至可以使用线性激励函数(请见第2章)。不过,实际应用中,在隐层和输出层使用线性激励函数并不能发挥多大的作用,因此我们希望将非线性函数引入到典型的神经网络中,以解决复杂问题。毕竟线性函数的组合得到的还是线性函数。
上一章中使用的逻辑斯谛激励函数(logistic activation function)可能是对人类大脑神经元概念最为近似的模拟:我们可以将其看作神经元是否被激活的概率。不过,当输入为极大的负值时,逻辑斯谛激励函数也会出问题,这种情况下它的输出会趋近于0。如果sigmoid激励函数的输出趋近于0,那么将会降低神经网络的学习速度,并且在训练过程中更容易陷入局部最小值。这也是人们喜欢在隐层使用双曲正切(hyperbolic tangent)函数作为激励函数的原因。在讨论双曲正切函数之前,我们先对逻辑斯谛函数做一个简单的概述,并且分析一下到底是什么特性使得它在多类别分类任务中起到了如此重要的作用。
13.2.1 逻辑斯谛函数概述
我们前面提到的逻辑斯谛函数,通常称作sigmoid函数,它实际上是sigmoid函数的一个特例。请回顾一下第3章中逻辑斯谛回归一节,在二类别分类任务中,我们使用逻辑斯谛函数对样本x属于正类别(类别1)的概率进行建模:
![]()
其中,标量z被定义为净输入:
![]()
其中,w0是偏置单元(当x0=1时在y轴上的截距)。再给出一个更为具体的例子:下列代码演示的是一个适用于二维数据点x的模型,其中w为模型的权重系数向量:

如果使用给定的特征值和权重系数来计算净输入,并用结果去激励逻辑斯谛神经元,我们将得到返回值0.707,意思就是给定的样本x属于正类的概率为70.7%。在第12章,我们使用独热编码技术计算包含多个逻辑斯谛激励单元的输出层的值。不过,正如下列示例代码所示,包含多个逻辑斯谛激励单元的输出层无法提供有意义、可解释的概率值:

正如输出结果所示,特定样本属于第一个类别的概率大概为88%,此样本属于第二个类别的概率约为58%,而它属于第三个类别的概率为90%。这明显让我们产生了疑惑:各类别的概率之和应该为100%。不过,实际上,比例的值在这里并非大问题,我们只是用模型来预测类标,而不用给出样本属于某个类别的概率。

不过,在某些情况下,在多类别分类中给出所属类别概率是非常有用的。在下一节,我们将介绍更一般化的逻辑斯谛函数——softmax函数,它可以在多类别分类任务中给出样本所属类别的概率。
13.2.2 通过softmax函数评估多类别分类任务中的类别概率
softmax函数是更加一般化的逻辑斯谛函数,在多类别分类(多类别逻辑斯谛回归)中,它使得我们能够计算有意义的类别隶属概率。在softmax中,分母是经归一化处理的所有M个线性函数之和,而分子为净输入z,二者的比值即为特定样本属于第i个类别的概率:
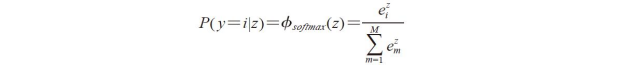
我们使用Python代码来完成一个softmax实例:

正如我们所预期的那样,各类别隶属概率之和为1。值得一提的是,样本属于第二个类别的概率接近于0,这是由于z和max(z)之间存在较大差距。不过总体预测结果与逻辑斯谛函数的结果一致。直观上看,将softmax函数看作是归一化的逻辑斯谛函数,有助于在多类别分类中对类别隶属做出有意义的预测。

13.2.3 通过双曲正切函数增大输出范围
另一个在人工神经网络隐层中经常用到的sigmoid函数是双曲正切(hyperbolic tangent,tanh)函数,它可以看作是经过缩放的逻辑斯谛函数。
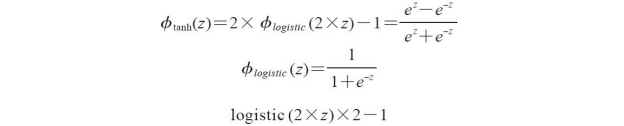
与逻辑斯谛函数相比,双曲正切函数的优势在于它输出值的范围更广,介于开区间(-1,1),这可以加速反向传播算法的收敛[1]。而逻辑斯谛函数返回值的开区间为(0,1)。为了对逻辑斯谛函数和双曲正切函数做个直观的比较,我们绘制出两个函数在同一区间中的图像:

从图中可以看出,两个S型曲线的形状非常类似;不过,tanh函数的输出范围是逻辑斯谛函数的2倍:
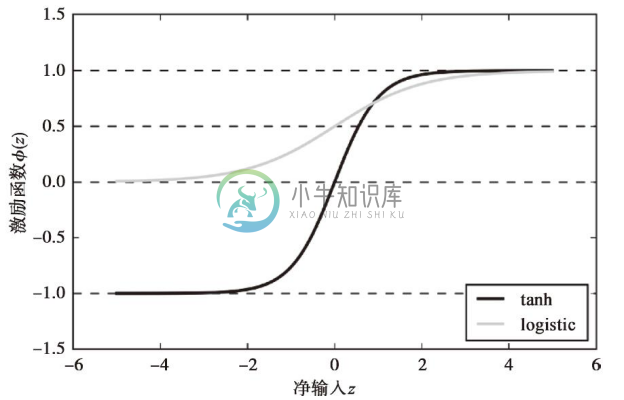
请注意,出于演示的需要,我们在本章中实现了logistic和tanh函数,在实际应用中,我们可以直接使用NumPy中的tanh函数以获得同样的结果:
![]()
此外,在SciPy的special模块中,已经实现了logistic函数:
![]()
我们已经了解了人工神经网络中常用的激励函数,最后,我们总结一下本书中出现过的多种不同的激励函数来结束本小节的内容。

[1] C. M. Bishop. Neural networks for pattern recognition. Oxford university press, 1995, pp. 500-501.

