10.3 基于最小二乘法构建线性回归模型
在本章开始时讨论过，可将线性回归模型看作通过训练数据的样本点来寻找一条最佳拟合直线。不过，在此既没有对最佳拟合做出定义，也没有研究拟合类似模型的各种技术。在接下来的小节中，我们将消除读者对上述问题的疑惑：通过最小二乘法（Ordinary Least Squares，OLS）估计回归曲线的参数，使得回归曲线到样本点垂直距离（残差或误差）的平方和最小。
10.3.1 通过梯度下降计算回归参数
回顾一下第2章中介绍的自适应线性神经元（Adaptive Linear Neuron，Adaline）：人工神经元中使用了一个线性激励函数，同时还定义了一个代价函数J（·），通过梯度下降（Gradient Descent，GD）、随机梯度下降（Stochastic Gradient Descent，GD）等优化算法使得代价函数最小，从而得到相应的权重。Adaline中的代价函数就是误差平方和（Sum of Squared Error，SSE），它等同于我们定义的OLS代价函数：
其中，
为通过
得到的预测值（注意，此处的系数1/2仅是为了方便推导GD更新规则）。本质上，OLS线性回归可以理解为无单位阶跃函数的Adaline，这样我们得到的是连续型的输出值，而不是以-1和1来代表的类标。为了说明两者的相似程度，使用第2章中实现的GD方法，并且移除其单位阶跃函数来实现我们第一个线性回归模型：
如果读者需要补习权重更新的内容——为何沿着与梯度相反的方向前进一步，请再复习第2章中的相关内容。
为了在实践中熟悉LinearRegressionGD类，我们使用了房屋数据集中的RM（房间数量）作为解释变量来训练模型以预测MEDV（房屋价格）。此外，为了使得梯度下降算法收敛性更佳，在此对相关变量做了标准化处理，代码如下：
第2章中曾介绍过，梯度下降算法能够进行收敛性检查，使用这类优化算法时，将代价看作迭代次数的函数（基于训练数据集），并将其绘制成图是个非常好的做法。简而言之，我们将再次绘制迭代次数对应的代价函数的值，以检查线性回归是否收敛：
从下图中可以看到，经过第5次迭代后，GD算法收敛了：
接下来，我们将线性回归曲线与训练数据拟合情况绘制成图。为达到此目的，我们定义了一个辅助函数用来绘制训练样本的散点图，同时绘制出相应的回归曲线：
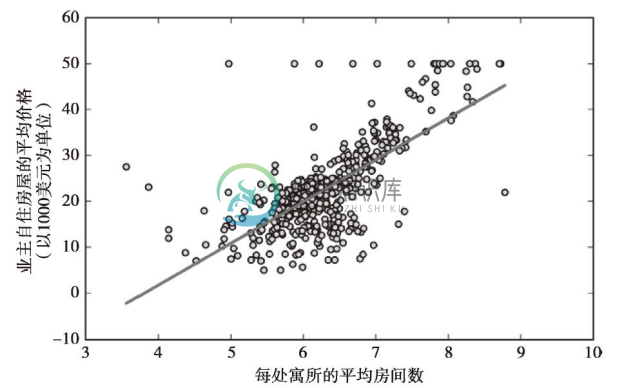
至此，我们使用lin_regplot函数绘制房间数与房屋价格之间的关系图：
正如下图所示，线性回归曲线反映出了一般趋势，随着房间数量的增加，房价呈增长趋势：
上述结论是基于直觉观察得到的，但是数据也同样告诉我们，房间数在很多情况下并不能很好地解释房价。本章后续内容将讨论如何量化回归模型的性能。有趣的是，我们观察到一条奇怪的直线y＝3，这意味着房价被限定了上界。在某些应用中，给出变量在原始取值区间上的预测值也是非常重要的。为了将预测价格缩放到以1000美元为价格单位的坐标轴上，我们使用了StandardScaler的inverse_transform方法：
上述代码中，我们使用了之前训练好的线性回归模型来预测带有5个房间的房屋价格。根据我们模型的预测，此房屋价值10840美元。
值得一提的是：对于经过标准化处理的变量，我们无需更新其截距的权重，因为它们在y轴上的截距始终为0。我们可以通过输出其权重来快速确认这一点：
10.3.2 使用scikit-learn估计回归模型的系数
上一小节中，我们实现了一个可用的回归分析模型。不过在实际应用中，我们可能会更关注如何高效地实现模型，例如，scikit-learn中的LinearRegression对象使用了LIBLINEAR库以及先进的优化算法，可以更好地使用经过标准化处理的变量。这正是特定应用所需要的：
执行上述代码后可见，使用经过标准化处理的RM和MEDV数据拟合scikit-learn中的LinearRegression模型得到了不同的模型系数。我绘制出MEDV与RM之间的关系图，并与GD算法实现的模型进行比较：
上述代码绘制出了训练数据和拟合模型的图像，从图中可看出，总体结果与GD算法实现的模型是一致的：
在大多数介绍统计科学的教科书中，都可以找到使用最小二乘法求解线性方程组的封闭方法：
其中，μy为真实目标值的均值，为经预测得到目标值的均值。
这种方法的优点在于：它一定能够分析找到最优解。不过，如果要处理的数据集量很大，公式中逆矩阵的计算成本会非常高，或者矩阵本身为奇异矩阵（不可逆），这就是在特定情况下我们更倾向于使用交互式方法的原因。
若读者对如何得到正规方程感兴趣，建议阅读Stephen Pollock博士在英国莱斯特大学演讲讲义中的章节“The Classical Linear Regression Model”，可通过链接http://www.le.ac.uk/users/dsgp1/COURSES/MESOMET/ECMETXT/06mesmet.pdf获取。