12.1 使用人工神经网络对复杂函数建模

优质

小牛编辑

120浏览

2023-12-01

我们在第2章中从人工神经元入手，开始了机器学习算法的探索。对于本章中将要讨论的多层人工神经网络来说，人工神经元是其构建的基石。人工神经网络的基本概念是建立在对人脑如何应对复杂问题的假想和模型构建上的。人工神经网络在近几年得到了普及，对它的研究最早可追溯到20世纪40年代，Warren McCulloch和Walter Pitt第一个给出了关于神经元如何工作的描述。Rosenblatt在20世纪50年代第一个实现了基于麦卡洛克-皮特（McCulloch-Pitt）神经元模型的感知器算法，在之后的几十年中，由于没有好的训练多层神经网络的算法，许多机器学习的研究人员和从业者逐渐对它失去了兴趣。直到1986年，D.E.Rumelhart、G.E.Hinton和R.J.Williams经过潜心研究，提出并推广了反向传播算法之后，才重新引起了人们对神经网络的重视。关于此算法的详细内容我们将在本章后续做进一步讨论^[1]。

在过去的十年中，神经网络研究领域的许多重大突破成就了当前的深度学习算法，此算法可以通过无类标数据训练的深度神经网络（多层神经网络）进行特征检测。神经网络不仅仅是学术领域的一个热门话题，连Facebook、微软及谷歌等大型科技公司都在人工神经网络和深度学习研究领域进行了大量的投入。时至今日，由于能够解决图像和语音识别等复杂问题，由深度学习算法所驱动的复杂神经网络被认为是最前沿的研究成果。我们日常生活中深度学习的常见例子有谷歌图片搜索和谷歌翻译，谷歌翻译作为一款智能手机应用，能够自动识别图片中的文字，并将其实时翻译为20多种语言^[2]。

当前一些主要的科技公司正在积极开发更多有趣的深度神经网络应用，如Facebook公司开发的给图片打标签的DeepFace^[3]，百度公司的DeepSpeech，它可以处理普通话语音查询^[4]。此外，制药行业近期也开始将深度学习技术用于新药研发和毒性预测，研究表明，这些新技术的性能远超过传统的虚拟筛选方法^[5]。

[1] Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (1986). Learning Representations by Backpropagating Errors. Nature 323 (6088): 533-536.

[2] http://googleresearch.blogspot.com/2015/07/how-google-translate-squeezes-deep.html.

[3] Y. Taigman, M. Yang, M. Ranzato, and L. Wolf. DeepFace: Closing the gap to human-level performance in face verification. In Computer Vision and Pattern Recognition CVPR, 2014 IEEE Conference, pages 1701-1708.

[4] A. Hannun, C. Case, J. Casper, B. Catanzaro, G. Diamos, E. Elsen, R. Prenger, S. Satheesh, S. Sengupta, A.Coates, et al. DeepSpeech: Scaling up end-to-end speech recognition. arXiv preprint arXiv:1412.5567, 2014.

[5] T. Unterthiner, A. Mayr, G. Klambauer, and S. Hochreiter. Toxicity prediction using deep learning. arXiv preprint arXiv:1503.01445, 2015.

12.1.1　单层神经网络回顾

本章涉及的内容主要是多层神经网络，包括其工作原理，以及如何对其进行训练以解决复杂问题等。不过在深入讨论多层神经网络结构之前，我们先简要回顾下第2章中介绍的单层神经网络的相关概念，即如下图所示的自适应线性神经元（Adaline）算法：

在第2章中，我们实现了用于二类别分类的Adaline算法，并通过梯度下降优化算法来学习模型的权重系数。训练集上的每一次迭代，我们使用如下更新规则来更新权重向量w：

换句话说，我们基于整个训练数据集来计算梯度，并沿着与梯度▽J（w）相反的方向前进以更新模型的权重。为了找到模型的最优权重，我们将待优化的目标函数定义为误差平方和（SSE）代价函数J（w）。此外，我们还为梯度增加了一个经过精心挑选的因子：学习速率η，在学习过程中用于权衡学习速度和代价函数全局最优点之间的关系。

在梯度下降优化过程中，我们在每次迭代后同时更新所有权重，并将权重向量w中各权值w_j的偏导定义为：

其中，y^（i）为特定样本x^（i）的真实类标，a^（i）为神经元的激励，它是Adaline在特定情形下的线性函数。此外，我们将激励函数φ（·）定义为：

其中，净输入z是输入与权重的线性组合，用于连接输入和输出层：

使用激励φ（z）来计算梯度更新时，我们定义了一个阈值函数（单位阶跃函数）将连续的输出值转换为二类别分类的预测类标：

请注意：尽管Adaline包含一个输入层和一个输出层，但由于两层之间只有单一的网络连接，因此仍旧称为单层神经网络。

12.1.2　多层神经网络架构简介

在本节，我们将看到如何将多个单独的神经元连接为一个多层前馈神经网络（multi-layer feedforward neural network）。这种特殊类型的网络也称作多层感知器（multi-layer perceptron，MLP）。下图解释了三层MLP的概念：一个输入层、一个隐层，以及一个输出层。隐层的所有单元完全连接到输入层上，同时输出层的单元也完全连接到了隐层中。如果网络中包含不止一个隐层，我们则称其为深度人工神经网络。

我们可以向MLP中加入任意数量的隐层来创建更深层的网络架构。实际上，可以将神经网络中的隐层数量及各单元看作是额外的超参，可以使用第6章中介绍过的交叉验证针对特定问题对它们进行优化。

不过，随着增加到网络中的隐层越来越多，通过反向传播算法计算得到的梯度误差也将变得越来越小。这个接近于不存在的梯度问题使得模型的学习非常具有挑战性。因此，特别发展出了针对此类深层神经网络架构的预处理算法，亦即所谓的深度学习。

如前面的图所示，我们将第l层中第i个激励单元记为，同时激励单元和为偏置单元（bias unit），我们均设定为1。输入层各单元的激励为输入加上偏置单元：

对于l层中的各单元，均通过一个权重系数连接到l＋1层中的所有单元上。例如，连接第l层中第k个单元与第l＋1层中第j个单元的连接可记作。请注意，中的上标i代表是第i个样本，而不是第i层。为了简洁起见，后续段落中我们将忽略上标i。

虽然对于二类别分类来说，输出层包含一个激励单元就已足够，但在前面的图中我们可以发现一个更加通用的神经网络形式，通过一对多技术（One-vs-ALL，OvA），可以将它推广到多类别分类上。为了更好理解它是如何工作的，请回忆一下我们在第4章中介绍的使用独热（one-hot）法来表示分类变量。例如，我们可以将鸢尾花数据集中的三个类标（0=Setosa,1=Versicolor,2=Virginica）表示如下：

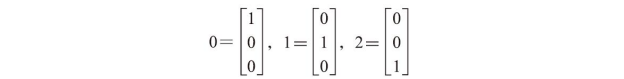
通过独热向量表示方法，我们可以处理数据集中包含任意多个类别的分类任务。

如果读者是第一次接触到神经网络表示方法，起初可能会对术语符号的标记（上标和下标）感到困惑。也许会疑惑为什么我们不使用，而是使用来表示连接第l层中第k个单元和第l＋1层中第j个单元的权重系数。这些乍看好像很古怪的内容在后续小节中，当使用向量来表示神经网络时将会非常有用。例如，我们将使用矩阵来表示连接输入层和隐层之间的权重，其中h为隐层的数量，而m+1为隐层中节点及偏置节点数量之和。真正理解并消化这种标识方法对于学习本章后续内容至关重要，我们通过下图来解释一下前面介绍过的3-4-3多层感知器：

12.1.3　通过正向传播构造神经网络

本节中，我们将使用正向传播（forward propagation）来计算多层感知器（MLP）模型的输出。为理解正向传播是如何通过学习来拟合多层感知器模型，我们将多层感知器的学习过程总结为三个简单步骤：

1）从输入层开始，通过网络向前传播（也就是正向传播）训练数据中的模式，以生成输出。

2）基于网络的输出，通过一个代价函数（稍后将有介绍）计算所需最小化的误差。

3）反向传播误差，计算其对于网络中每个权重的导数，并更新模型。

最终，通过对多层感知器模型权重的多次迭代和学习，我们使用正向传播来计算网络的输出，并使用阈值函数获得独热法所表示的预测类标，独热表示法介绍详见上节。

现在，让我们根据正向传播算法逐步从训练数据的模式中生成一个输出。由于隐层每个节点均完全连接到所有输入层节点，我们首先通过以下公式计算的激励：

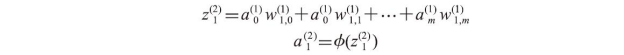
其中，为净输入，φ（·）为激励函数，此函数必须是可微的，以方便根据梯度方法学习得到连接神经元的权重。为了解决图像分类等复杂问题，我们需要在多层感知器模型中使用非线性激励函数，例如，在第3章的逻辑斯谛回归中所使用的sigmoid激励函数：

我们应该还记得，sigmoid函数的图像为S型曲线，它可以将净输入映射到一个介于[0,1]区间的逻辑斯谛分布上去，分布的原点为z＝0.5处，如下图所示：

多层感知器是一个典型的前馈人工神经网络。与本章后续要讨论的递归神经网络不同，此处的前馈是指每一层的输出都直接作为下一层的输入。由于此网络架构中，人工神经元是典型的sigmoid单元，而不是感知器，因此多层感知器这个词听起来有些不够贴切。直观上说，我们可以将多层感知器中的神经元看作是返回值位于[0,1]连续区间上的逻辑斯谛回归单元。

为了提高代码的执行效率和可读性，我们将使用线性代数中的基本概念，并以紧凑的方式实现一个激励单元：借助NumPy使用向量化的代码，而不是使用效率低下的Python多层for循环嵌套：