python实现多层感知器MLP（基于双月数据集）

本文实例为大家分享了python实现多层感知器MLP的具体代码，供大家参考，具体内容如下

1、加载必要的库，生成数据集

import math
import random
import matplotlib.pyplot as plt
import numpy as np
class moon_data_class(object):
  def __init__(self,N,d,r,w):
    self.N=N
    self.w=w
   
    self.d=d
    self.r=r
  
  
  def sgn(self,x):
    if(x>0):
      return 1;
    else:
      return -1;
    
  def sig(self,x):
    return 1.0/(1+np.exp(x))
  
    
  def dbmoon(self):
    N1 = 10*self.N
    N = self.N
    r = self.r
    w2 = self.w/2
    d = self.d
    done = True
    data = np.empty(0)
    while done:
      #generate Rectangular data
      tmp_x = 2*(r+w2)*(np.random.random([N1, 1])-0.5)
      tmp_y = (r+w2)*np.random.random([N1, 1])
      tmp = np.concatenate((tmp_x, tmp_y), axis=1)
      tmp_ds = np.sqrt(tmp_x*tmp_x + tmp_y*tmp_y)
      #generate double moon data ---upper
      idx = np.logical_and(tmp_ds > (r-w2), tmp_ds < (r+w2))
      idx = (idx.nonzero())[0]
   
      if data.shape[0] == 0:
        data = tmp.take(idx, axis=0)
      else:
        data = np.concatenate((data, tmp.take(idx, axis=0)), axis=0)
      if data.shape[0] >= N:
        done = False
    #print (data)
    db_moon = data[0:N, :]
    #print (db_moon)
    #generate double moon data ----down
    data_t = np.empty([N, 2])
    data_t[:, 0] = data[0:N, 0] + r
    data_t[:, 1] = -data[0:N, 1] - d
    db_moon = np.concatenate((db_moon, data_t), axis=0)
    return db_moon

2、定义激活函数

def rand(a,b):
  return (b-a)* random.random()+a

def sigmoid(x):
  #return np.tanh(-2.0*x)
  return 1.0/(1.0+math.exp(-x))
def sigmoid_derivate(x):
  #return -2.0*(1.0-np.tanh(-2.0*x)*np.tanh(-2.0*x))
  return x*(1-x) #sigmoid函数的导数

3、定义神经网络

class BP_NET(object):
  def __init__(self):
    self.input_n = 0
    self.hidden_n = 0
    self.output_n = 0
    self.input_cells = []
    self.bias_input_n = []
    self.bias_output = []
    self.hidden_cells = []
    self.output_cells = []
    self.input_weights = []
    self.output_weights = []
    
    self.input_correction = []
    self.output_correction = []
  
  def setup(self, ni,nh,no):
    self.input_n = ni+1#输入层+偏置项
    self.hidden_n = nh
    self.output_n = no
    self.input_cells = [1.0]*self.input_n
    self.hidden_cells = [1.0]*self.hidden_n
    self.output_cells = [1.0]*self.output_n
    
    self.input_weights = make_matrix(self.input_n,self.hidden_n)
    self.output_weights = make_matrix(self.hidden_n,self.output_n)
    
    for i in range(self.input_n):
      for h in range(self.hidden_n):
        self.input_weights[i][h] = rand(-0.2,0.2)
    
    for h in range(self.hidden_n):
      for o in range(self.output_n):
        self.output_weights[h][o] = rand(-2.0,2.0)
    
    self.input_correction = make_matrix(self.input_n , self.hidden_n)
    self.output_correction = make_matrix(self.hidden_n,self.output_n)
        
  def predict(self,inputs):
    for i in range(self.input_n-1):
      self.input_cells[i] = inputs[i]
    
    for j in range(self.hidden_n):
      total = 0.0
      for i in range(self.input_n):
        total += self.input_cells[i] * self.input_weights[i][j]
      self.hidden_cells[j] = sigmoid(total)
      
    for k in range(self.output_n):
      total = 0.0
      for j in range(self.hidden_n):
        total+= self.hidden_cells[j]*self.output_weights[j][k]# + self.bias_output[k]
        
      self.output_cells[k] = sigmoid(total)
    return self.output_cells[:]
  
  def back_propagate(self, case,label,learn,correct):
    #计算得到输出output_cells
    self.predict(case)
    output_deltas = [0.0]*self.output_n
    error = 0.0
    #计算误差 = 期望输出-实际输出
    for o in range(self.output_n):
      error = label[o] - self.output_cells[o] #正确结果和预测结果的误差：0,1，-1
      output_deltas[o]= sigmoid_derivate(self.output_cells[o])*error#误差稳定在0~1内
 
    hidden_deltas = [0.0] * self.hidden_n
    for j in range(self.hidden_n):
      error = 0.0
      for k in range(self.output_n):
        error+= output_deltas[k]*self.output_weights[j][k]
      hidden_deltas[j] = sigmoid_derivate(self.hidden_cells[j])*error 

    for h in range(self.hidden_n):
      for o in range(self.output_n):
        change = output_deltas[o]*self.hidden_cells[h]
        #调整权重：上一层每个节点的权重学习*变化+矫正率
        self.output_weights[h][o] += learn*change 
    #更新输入->隐藏层的权重
    for i in range(self.input_n):
      for h in range(self.hidden_n):
        change = hidden_deltas[h]*self.input_cells[i]
        self.input_weights[i][h] += learn*change 
      
      
    error = 0
    for o in range(len(label)):
      for k in range(self.output_n):
        error+= 0.5*(label[o] - self.output_cells[k])**2
      
    return error
    
  def train(self,cases,labels, limit, learn,correct=0.1):

    for i in range(limit):        
      error = 0.0
      # learn = le.arn_speed_start /float(i+1)    
      for j in range(len(cases)):
        case = cases[j]
        label = labels[j] 
             
        error+= self.back_propagate(case, label, learn,correct)
      if((i+1)%500==0):
        print("error:",error)
        
  def test(self): #学习异或

    
    N = 200
    d = -4
    r = 10
    width = 6
    
    data_source = moon_data_class(N, d, r, width)
    data = data_source.dbmoon()
    

    
    # x0 = [1 for x in range(1,401)]
    input_cells = np.array([np.reshape(data[0:2*N, 0], len(data)), np.reshape(data[0:2*N, 1], len(data))]).transpose()
    
    labels_pre = [[1.0] for y in range(1, 201)]
    labels_pos = [[0.0] for y in range(1, 201)]
    labels=labels_pre+labels_pos
    
    self.setup(2,5,1) #初始化神经网络：输入层，隐藏层，输出层元素个数
    self.train(input_cells,labels,2000,0.05,0.1) #可以更改
    
    test_x = []
    test_y = []
    test_p = []
    
    y_p_old = 0
  
    for x in np.arange(-15.,25.,0.1):

      for y in np.arange(-10.,10.,0.1):
        y_p =self.predict(np.array([x, y]))

        if(y_p_old <0.5 and y_p[0] > 0.5):
          test_x.append(x)
          test_y.append(y)
          test_p.append([y_p_old,y_p[0]])
        y_p_old = y_p[0]
    #画决策边界
    plt.plot( test_x, test_y, 'g--')  
    plt.plot(data[0:N, 0], data[0:N, 1], 'r*', data[N:2*N, 0], data[N:2*N, 1], 'b*')
    plt.show()  
          

if __name__ == '__main__':
  nn = BP_NET()
  nn.test()

4、运行结果

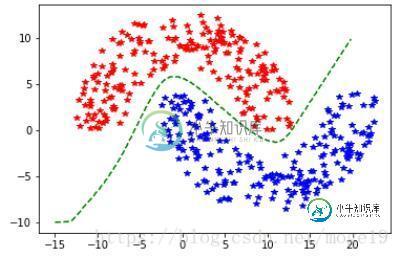
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。