4.2.5 绘制贝塞尔曲线

贝塞尔曲线于1959年，由法国物理学家与数学家Paul de Casteljau所发明，于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，并用于汽车的车身设计。贝赛尔曲线为计算机矢量图形学奠定了基础，它的主要意义在于无论是直线或曲线都能在数学上予以描述。

贝塞尔曲线分为两种：二次贝塞尔曲线和三次贝塞尔曲线。

quadraticCurveTo()方法绘制二次贝塞尔曲线

二次贝塞尔曲线是一种二次曲线，它只能向一个方向弯曲，由三个点来定义：两个锚点及一个控制点，控制点用来控制曲线的形状。

二次贝塞尔曲线由三个特征切线定义，曲线的第一部分与上下文点和控制点形成的虚线相切，曲线的顶部与midpoint 1和midpoint 2形成的虚线相切，曲线的最后部分与控制点和终点形成的虚线相切。如图 4‑10 所示：

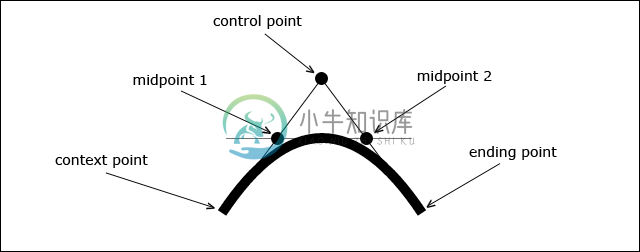
在Canvas中，二次贝塞尔曲线的两个锚点分别是上下文点和终点，而起点是已知的。因此只需知道控制点和终点，就能唯一确定一条二次贝塞尔曲线。绘制方法为：

quadraticCurveTo(controlX, controlY, endingPointX, endingPointY)

以下实例使用quadraticCurveTo(cpx,cpy,x,y)方法来绘制一条二次曲线，其中，起点是由上下文维护，控制点为(cpx,cpy)，终点为(x,y)。

var cpx = 150, cpy = 50, x = 200, y = 250;
context.lineWidth = 10;
context.beginPath();
context.moveTo(50,250);
context.quadraticCurveTo(cpx,cpy,x,y);
context.stroke();

上述代码的运行结果如图 4‑11 所示：

bezierCurveTo()方法绘制三次贝塞尔曲线

由于二次贝塞尔曲线只有一个控制点，所以它永远只能画向一个方向弯曲的弧线，画不出S形曲线。要绘制S形曲线，还需要使用三次贝塞尔曲线。

三次贝塞尔曲线是一种三次曲线，由四个点来定义：两个锚点及两个控制点，两个控制点用来控制曲线的形状。

贝塞尔曲线由5条特征切线定义。曲线的第一部分与从上下文点和第一个控制点形成的虚线相切，曲线的第二部分与midpoint 1和midpoint 3形成的虚线相切，曲线的顶部与midpoint 2和midpoint 4形成的虚线相切，曲线的第四部分与midpoint 3和midpoint 5形成的虚线相切，曲线的最后部分与第二个控制点和终点形成的虚线相切。如图 4‑12 所示：

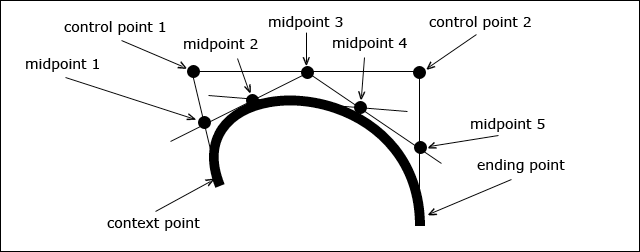
Canvas中的三次贝塞尔曲线由上下文点、两个控制点、一个终点定义。绘制方法为：

bezierCurveTo(controlX1, controlY1, controlX2, controlY2, endPointX, endPointY)

以下实例使用bezierCurveTo(cp1x,cp1y, cp2x,cp2y,x,y)方法来绘制一条二次曲线，其中，起点是由上下文维护，控制点为(cp1x,cp1y)和(cp2x,cp2y)，终点为(x,y)。

var cp1x = 200, cp1y = 260, cp2x = 380, cp2y = 10, x = 420, y = 180;
context.lineWidth = 10;
context.beginPath();
context.moveTo(180, 100);
context.bezierCurveTo(cp1x,  cp1y,  cp2x,  cp2y,  x,  y);
context.stroke();

上述代码的运行结果如图 4‑13 所示：