贝塞尔曲线到点的垂直线

Question

我需要得到一条三次(2D)bezier曲线B(t)的点Q，其中从点Q到另一个给定点P的直线与bezier曲线垂直相交。

• 我知道:P，B(t)
• 我寻找：Q（基本上我想要g的斜率，但当我知道Q时，我可以很容易地计算出来，但g的斜率已经足够了）

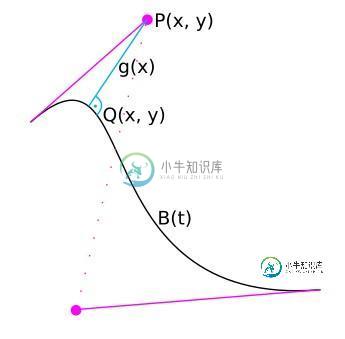
注意，我认为这个ansatz是错误的。这只是为了完整性而包括的。

其中B(x)是笛卡尔坐标系下的bezier曲线，B'(x)是（笛卡尔坐标系下的）导数，k是与y轴的交点。要得到g(x)的斜率，必须求解

为了计算B(x)，我们必须求解t的B(t)，然后将其插回B(t)中。所以在bezier曲线上的每一点上都有如下关系

这也适用于导数b'(t)。

其中A₀=(P₁-P₀)_X，A₁=(P₂-P₂)_X和A₂=(P₃)。将*t_i*s插入b(t)中（wolfram alpha用于t₁，wolfram alpha用于t₂，wolfram alpha用于t₃)

接下来的事情是用y=b'(x)和第二个方程，消除x，但我不知道怎么消除，甚至不知道这是否可能。

Answer 1

你已经知道Bezier曲线的导数--它描述了曲线的切线。这个切线应该垂直于qp向量。因此，此时需要编写向量pq和切向量t的组件

PQx = (1-t)^3 * P0.x + 3*t*(1-t)^2*P1.x  ... - P.x
PQy = (1-t)^3 * P0.y + ... - P.y
Tx = 3*(1-t)^2 * (P1.x - P0.x).... and so on
Ty = ....

并给出向量T和QP的点积方程（垂直向量的点积为零）：

 PQx * Tx + PQy * Ty = 0

现在打开括号，得到未知t的5次方程。