登录
当前位置： 首页 > 编程笔记 >

Android Path绘制贝塞尔曲线实现QQ拖拽泡泡

公冶渝
2023-03-14
本文向大家介绍Android Path绘制贝塞尔曲线实现QQ拖拽泡泡，包括了Android Path绘制贝塞尔曲线实现QQ拖拽泡泡的使用技巧和注意事项，需要的朋友参考一下

这两天学习了使用Path绘制贝塞尔曲线相关，然后自己动手做了一个类似QQ未读消息可拖拽的小气泡，效果图如下：

最终效果图
接下来一步一步的实现整个过程。

基本原理

其实就是使用Path绘制三点的二次方贝塞尔曲线来完成那个妖娆的曲线的。然后根据触摸点不断绘制对应的圆形，根据距离的改变改变原始固定圆形的半径大小。最后就是松手后返回或者爆裂的实现。

Path介绍：

顾名思义，就是一个路径的意思，Path里面有很多的方法，本次设计主要用到的相关方法有

  1. moveTo() 移动Path到一个指定的点
  2. quadTo() 绘制二次贝塞尔曲线，接收两个点，第一个是控制弧度的点，第二个是终点。
  3. lineTo() 就是连线
  4. close() 闭合Path路径，
  5. reset() 重置Path的相关设置

Path入门热身：

path.reset();
 path.moveTo(200, 200);
 //第一个坐标是对应的控制的坐标，第二个坐标是终点坐标
 path.quadTo(400, 250, 600, 200);

 canvas.drawPath(path, paint);
 canvas.translate(0, 200);
 //调用close,就会首尾闭合连接
 path.close();
 canvas.drawPath(path, paint);

记得不要在onDraw方法中new Path或者 Paint哟！

Path

具体实现拆分：

其实整个过程就是绘制了两个贝塞尔二次曲线的的闭合Path路径，然后在上面添加两个圆形。

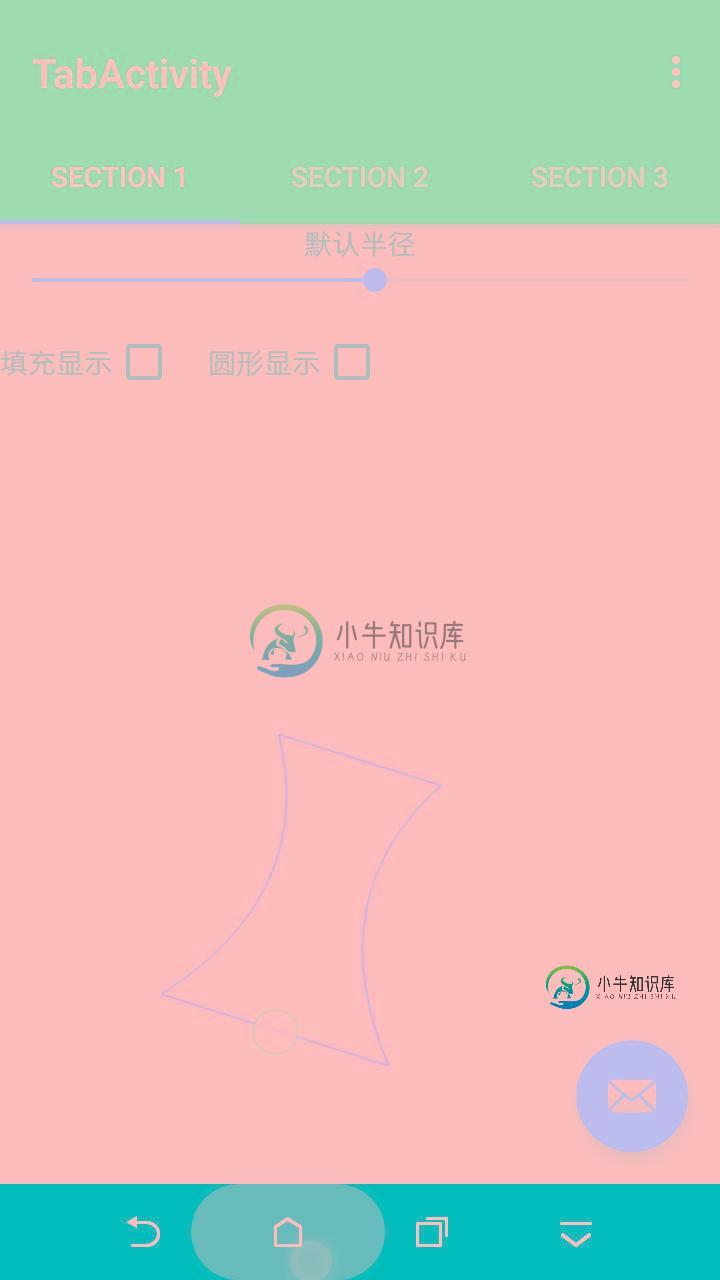
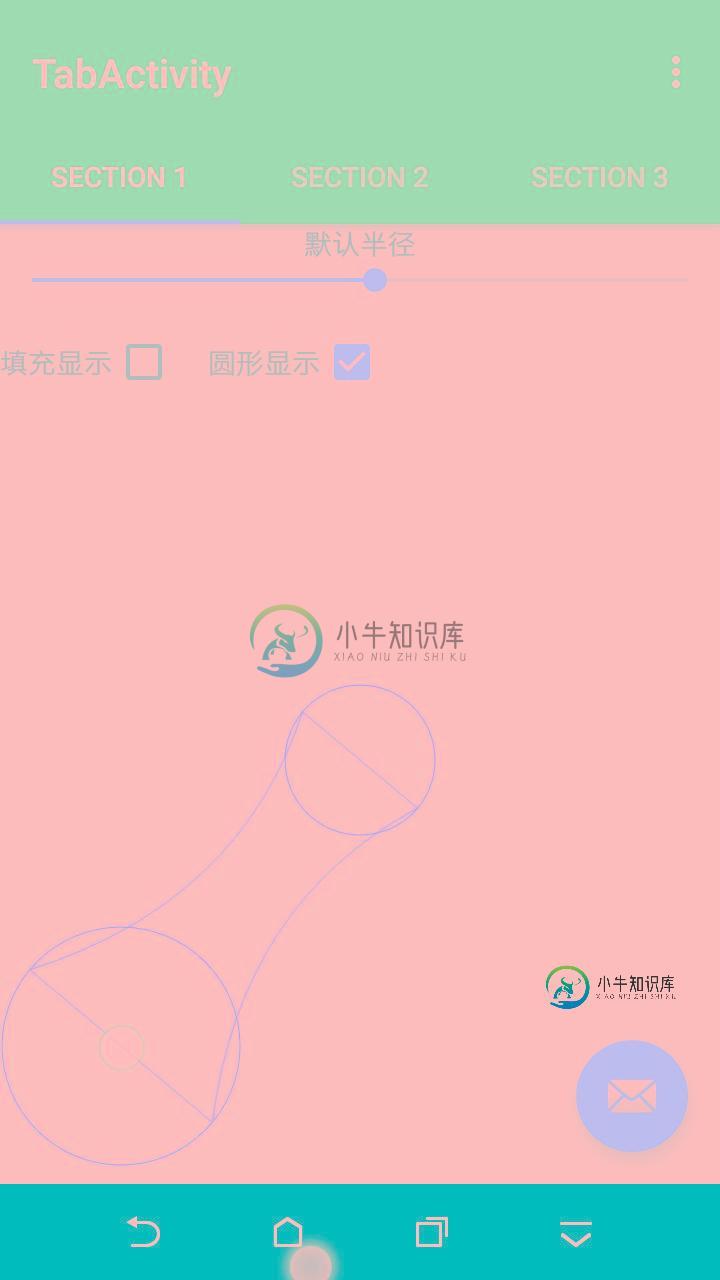
闭合的Path 路径实现从左上点画二次贝塞尔曲线到左下点，左下点连线到右下点，右下点二次贝塞尔曲线到右上点，最后闭合一下!!

相关坐标的确定

这是这次里面的难点之一，因为涉及到了数学里面的一个sin,cos,tan等等，我其实也忘完了，然后又脑补了一下，废话不多说，

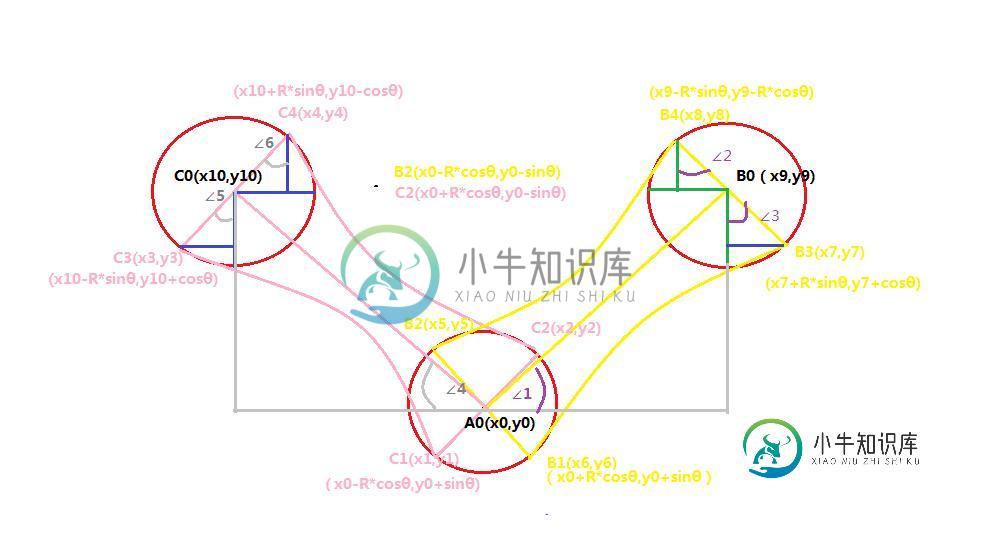
为什么自己要亲自去画一下呢，因为画了你才知道，在360旋转的过程中，角标体系是有两套的，如果就使用一套来画的话，就画出现在旋转的过程中曲线重叠在一起的情况！

问题已经抛出来了，接下来直接看看代码实现！

角度确定

根据贴出来的原理图可以知道，我们可以使用起始圆心坐标和拖拽的圆心坐标，根据反正切函数来得到具体的弧度。


int dy = Math.abs(CIRCLEY - startY);
int dx = Math.abs(CIRCLEX - startX);
 angle = Math.atan(dy * 1.0 / dx);

ok,这里的startX,Y就是移动过程中的坐标。angle就是得到的对应的弧度（角度）。

相关Path绘制

前面已经提到在旋转的过程中有两套坐标体系，一开始我也很纠结这个坐标体系要怎么确定，后面又恍然大悟，其实相当于就是一三象限正比例增长，二四象限，反比例增长。

flag = (startY - CIRCLEY  ) * (startX- CIRCLEX ) <= 0;
 //增加一个flag,用于判断使用哪种坐标体系。

最最重要的来了，绘制相关的Path路径！

 

path.reset();
 if (flag) {
  //第一个点
 path.moveTo((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY - Math.cos(angle) * ORIGIN_RADIO));

 path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (startX - Math.sin(angle) * DRAG_RADIO), (float) (startY - Math.cos(angle) * DRAG_RADIO));
path.lineTo((float) (startX + Math.sin(angle) * DRAG_RADIO), (float) (startY + Math.cos(angle) * DRAG_RADIO));

path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (CIRCLEX + Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY + Math.cos(angle) * ORIGIN_RADIO));
path.close();
canvas.drawPath(path, paint);
 } else {
  //第一个点
  path.moveTo((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY + Math.cos(angle) * ORIGIN_RADIO));

  path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (startX - Math.sin(angle) * DRAG_RADIO), (float) (startY + Math.cos(angle) * DRAG_RADIO));
  path.lineTo((float) (startX + Math.sin(angle) * DRAG_RADIO), (float) (startY - Math.cos(angle) * DRAG_RADIO));

  path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (CIRCLEX + Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY - Math.cos(angle) * ORIGIN_RADIO));
  path.close();
  canvas.drawPath(path, paint);
 }

这里的代码就是把图片上相关的数学公式Java化而已！

到这里，其实主要的工作就完成的差不多了！

接下来，设置paint 为填充的效果,最后再画两个圆

paint.setStyle(Paint.Style.FILL)
 canvas.drawCircle(CIRCLEX, CIRCLEY, ORIGIN_RADIO, paint);//默认的
 canvas.drawCircle(startX == 0 ? CIRCLEX : startX, startY == 0 ? CIRCLEY : startY, DRAG_RADIO, paint);//拖拽的

就可以绘制出想要的效果了！

这里不得不再说说onTouch的处理！

case MotionEvent.ACTION_DOWN://有事件先拦截再说！！
   getParent().requestDisallowInterceptTouchEvent(true);
   CurrentState = STATE_IDLE;
   animSetXY.cancel();
   startX = (int) ev.getX();
   startY = (int) ev.getRawY();
   break;

处理一下事件分发的坑！

测量和布局

这样基本过得去了，但是我们的布局什么的还没有处理，math_parent是万万没法使用到具体项目当中去的！
测量的时候，如果发现不是精准模式，那么都手动去计算出需要的宽度和高度。

@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {

 int modeWidth = MeasureSpec.getMode(widthMeasureSpec);
 int modeHeight = MeasureSpec.getMode(heightMeasureSpec);
 if (modeWidth == MeasureSpec.UNSPECIFIED || modeWidth == MeasureSpec.AT_MOST) {
  widthMeasureSpec = MeasureSpec.makeMeasureSpec(DEFAULT_RADIO * 2, MeasureSpec.EXACTLY);
 }
 if (modeHeight == MeasureSpec.UNSPECIFIED || modeHeight == MeasureSpec.AT_MOST) {
  heightMeasureSpec = MeasureSpec.makeMeasureSpec(DEFAULT_RADIO * 2, MeasureSpec.EXACTLY);
 }
 super.onMeasure(widthMeasureSpec, heightMeasureSpec);
}

然后在布局变化时，获取相关坐标，确定初始圆心坐标：

@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
 super.onSizeChanged(w, h, oldw, oldh);
 CIRCLEX = (int) ((w) * 0.5 + 0.5);
 CIRCLEY = (int) ((h) * 0.5 + 0.5);
}

然后清单文件里面就可以这样配置了：

<com.lovejjfg.circle.DragBubbleView
 android:id="@+id/dbv"
 android:layout_width="wrap_content"
 android:layout_height="wrap_content"
 android:layout_gravity="center"/>

这样之后，又会出现一个问题，那就是wrap_content 之后，这个View能绘制的区域只有自身那么大了，拖拽了都看不见了！这个坑怎么办呢，其实很简单，父布局加上android:clipChildren="false" 的属性！
这个坑也算是解决了！！

相关状态的确定

我们是不希望它可以无限的拖拽的，就是有一个拖拽的最远距离，还有就是放手后的返回，爆裂。那么对应的，这里需要确定几种状态：

private final static int STATE_IDLE = 1;//静止的状态
 private final static int STATE_DRAG_NORMAL = 2;//正在拖拽的状态
 private final static int STATE_DRAG_BREAK = 3;//断裂后的拖拽状态
 private final static int STATE_UP_BREAK = 4;//放手后的爆裂的状态
 private final static int STATE_UP_BACK = 5;//放手后的没有断裂的返回的状态
 private final static int STATE_UP_DRAG_BREAK_BACK = 6;//拖拽断裂又返回的状态
 private int CurrentState = STATE_IDLE;

private int MIN_RADIO = (int) (ORIGIN_RADIO * 0.4);//最小半径
 private int MAXDISTANCE = (int) (MIN_RADIO * 13);//最远的拖拽距离

确定好这些之后，在move的时候，就要去做相关判断了：

case MotionEvent.ACTION_MOVE://移动的时候
   startX = (int) ev.getX();
   startY = (int) ev.getY();

   updatePath();
   invalidate();
   break;

private void updatePath() {
 int dy = Math.abs(CIRCLEY - startY);
 int dx = Math.abs(CIRCLEX - startX);

 double dis = Math.sqrt(dy * dy + dx * dx);
 if (dis <= MAXDISTANCE) {//增加的情况，原始半径减小
  if (CurrentState == STATE_DRAG_BREAK || CurrentState == STATE_UP_DRAG_BREAK_BACK) {
   CurrentState = STATE_UP_DRAG_BREAK_BACK;
  } else {
   CurrentState = STATE_DRAG_NORMAL;
  }
  ORIGIN_RADIO = (int) (DEFAULT_RADIO - (dis / MAXDISTANCE) * (DEFAULT_RADIO - MIN_RADIO));
  Log.e(TAG, "distance: " + (int) ((1 - dis / MAXDISTANCE) * MIN_RADIO));
  Log.i(TAG, "distance: " + ORIGIN_RADIO);
 } else {
  CurrentState = STATE_DRAG_BREAK;
 }
//  distance = dis;
 flag = (startY - CIRCLEY) * (startX - CIRCLEX) <= 0;
 Log.i("TAG", "updatePath: " + flag);
 angle = Math.atan(dy * 1.0 / dx);
}

updatePath() 的方法之前已经看过部分了，这次的就是完整的。
这里做的事就是根据拖拽的距离更改相关的状态，并根据百分比来修改原始圆形的半径大小。还有就是之前介绍的确定相关的弧度！

最后放手的时候：

case MotionEvent.ACTION_UP:
   if (CurrentState == STATE_DRAG_NORMAL) {
    CurrentState = STATE_UP_BACK;
    valueX.setIntValues(startX, CIRCLEX);
    valueY.setIntValues(startY, CIRCLEY);
    animSetXY.start();
   } else if (CurrentState == STATE_DRAG_BREAK) {
    CurrentState = STATE_UP_BREAK;
    invalidate();
   } else {
    CurrentState = STATE_UP_DRAG_BREAK_BACK;
    valueX.setIntValues(startX, CIRCLEX);
    valueY.setIntValues(startY, CIRCLEY);
    animSetXY.start();
   }
   break;

自动返回这里使用到的 ValueAnimator，

animSetXY = new AnimatorSet();

 valueX = ValueAnimator.ofInt(startX, CIRCLEX);
 valueY = ValueAnimator.ofInt(startY, CIRCLEY);
 animSetXY.playTogether(valueX, valueY);
 valueX.setDuration(500);
 valueY.setDuration(500);
 valueX.setInterpolator(new OvershootInterpolator());
 valueY.setInterpolator(new OvershootInterpolator());
 valueX.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
  @Override
  public void onAnimationUpdate(ValueAnimator animation) {
   startX = (int) animation.getAnimatedValue();
   Log.e(TAG, "onAnimationUpdate-startX: " + startX);
   invalidate();
  }

 });
 valueY.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
  @Override
  public void onAnimationUpdate(ValueAnimator animation) {
   startY = (int) animation.getAnimatedValue();
   Log.e(TAG, "onAnimationUpdate-startY: " + startY);
   invalidate();

  }
 });

最后在看看完整的onDraw方法吧！

@Override
protected void onDraw(Canvas canvas) {
 switch (CurrentState) {
  case STATE_IDLE://空闲状态，就画默认的圆
   if (showCircle) {
    canvas.drawCircle(CIRCLEX, CIRCLEY, ORIGIN_RADIO, paint);//默认的
   }
   break;
  case STATE_UP_BACK://执行返回的动画
  case STATE_DRAG_NORMAL://拖拽状态 画贝塞尔曲线和两个圆
   path.reset();
   if (flag) {
    //第一个点
    path.moveTo((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY - Math.cos(angle) * ORIGIN_RADIO));

    path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (startX - Math.sin(angle) * DRAG_RADIO), (float) (startY - Math.cos(angle) * DRAG_RADIO));
    path.lineTo((float) (startX + Math.sin(angle) * DRAG_RADIO), (float) (startY + Math.cos(angle) * DRAG_RADIO));

    path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (CIRCLEX + Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY + Math.cos(angle) * ORIGIN_RADIO));
    path.close();
    canvas.drawPath(path, paint);
   } else {
    //第一个点
    path.moveTo((float) (CIRCLEX - Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY + Math.cos(angle) * ORIGIN_RADIO));

    path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (startX - Math.sin(angle) * DRAG_RADIO), (float) (startY + Math.cos(angle) * DRAG_RADIO));
    path.lineTo((float) (startX + Math.sin(angle) * DRAG_RADIO), (float) (startY - Math.cos(angle) * DRAG_RADIO));

    path.quadTo((float) ((startX + CIRCLEX) * 0.5), (float) ((startY + CIRCLEY) * 0.5), (float) (CIRCLEX + Math.sin(angle) * ORIGIN_RADIO), (float) (CIRCLEY - Math.cos(angle) * ORIGIN_RADIO));
    path.close();
    canvas.drawPath(path, paint);
   }
   if (showCircle) {
    canvas.drawCircle(CIRCLEX, CIRCLEY, ORIGIN_RADIO, paint);//默认的
    canvas.drawCircle(startX == 0 ? CIRCLEX : startX, startY == 0 ? CIRCLEY : startY, DRAG_RADIO, paint);//拖拽的
   }
   break;

  case STATE_DRAG_BREAK://拖拽到了上限，画拖拽的圆:
  case STATE_UP_DRAG_BREAK_BACK:
   if (showCircle) {
    canvas.drawCircle(startX == 0 ? CIRCLEX : startX, startY == 0 ? CIRCLEY : startY, DRAG_RADIO, paint);//拖拽的
   }
   break;

  case STATE_UP_BREAK://画出爆裂的效果
   canvas.drawCircle(startX - 25, startY - 25, 10, circlePaint);
   canvas.drawCircle(startX + 25, startY + 25, 10, circlePaint);
   canvas.drawCircle(startX, startY - 25, 10, circlePaint);
   canvas.drawCircle(startX, startY, 18, circlePaint);
   canvas.drawCircle(startX - 25, startY, 10, circlePaint);
   break;

 }


}

到这里，成品就出来了！！

总结：

1、确定默认圆形的坐标；
2、根据move的情况，实时获取最新的坐标，根据移动的距离（确定出角度），更新相关的状态，画出相关的Path路径。超出上限，不再画Path路径。
3、松手时，根据相关的状态，要么带Path路径执行动画返回，要么不带Path路径直接返回，要么直接爆裂！

以上就是用Android Path 绘制贝塞尔曲线的示例，后续继续补充相关文章，谢谢大家对本站的支持！

 类似资料：
  • Android使用贝塞尔曲线仿QQ聊天消息气泡拖拽效果

    本文向大家介绍Android使用贝塞尔曲线仿QQ聊天消息气泡拖拽效果，包括了Android使用贝塞尔曲线仿QQ聊天消息气泡拖拽效果的使用技巧和注意事项，需要的朋友参考一下 本文实例为大家分享了Android仿QQ聊天消息气泡拖拽效果展示的具体代码，供大家参考，具体内容如下 先画圆，都会吧。代码如下： 效果 拖拽的另个一圆就不画了，效果的实现主要是计算两个点之间的拖拽区域，如下图： 求出区域之后，使

  • Android贝塞尔曲线实现消息拖拽消失

    本文向大家介绍Android贝塞尔曲线实现消息拖拽消失，包括了Android贝塞尔曲线实现消息拖拽消失的使用技巧和注意事项，需要的朋友参考一下 写在前头 写消息拖拽效果的文章不少，但是大部分都把自定义View写死了，我们要实现的是传入一个View，每个View都可以实现拖拽消失爆炸的效果，当然我也是站在巨人的肩膀上来学习的。但个人觉得程序员本就应该敢于学习和借鉴。 源码地址：源码Github地址

  • 4.2.5 绘制贝塞尔曲线

    贝塞尔曲线于1959年，由法国物理学家与数学家Paul de Casteljau所发明，于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，并用于汽车的车身设计。贝赛尔曲线为计算机矢量图形学奠定了基础，它的主要意义在于无论是直线或曲线都能在数学上予以描述。 贝塞尔曲线分为两种：二次贝塞尔曲线和三次贝塞尔曲线。 quadraticCurveTo()方法绘制二次贝塞尔曲线

  • 1.4 绘制贝塞尔曲线

    如果二次曲线不能满足你的需要，贝塞尔曲线可能会满足你。贝塞尔曲线又称三次曲线，是HTML5画布API所能支持的最高级的曲线。 图1-7 绘制贝塞尔曲线 绘制步骤 按照以下步骤绘制任意贝塞尔曲线： 1. 定义2D画布并设置曲线样式： window.onload  = function(){ var canvas  = document.getElementById("myCanvas");

  • 贝塞尔曲线

    贝塞尔曲线用于计算机图形绘制形状，CSS 动画和许多其他地方。 它们其实非常简单，值得学习一次并且在矢量图形和高级动画的世界里非常受用。 控制点 贝塞尔曲线由控制点定义。 这些点可能有 2、3、4 或更多。 例如，两点曲线： 三点曲线： 四点曲线： 如果仔细观察这些曲线，你会立即注意到： 控制点不总是在曲线上这是非常正常的，稍后我们将看到曲线是如何构建的。 曲线的阶次等于控制点的数量减一。 对于两

  • 使用HTML5画布绘制贝塞尔曲线

    本文向大家介绍使用HTML5画布绘制贝塞尔曲线，包括了使用HTML5画布绘制贝塞尔曲线的使用技巧和注意事项，需要的朋友参考一下 是的，请使用HTML canvas方法在HTML5中绘制Bezier曲线。 示例 您可以尝试运行以下代码以使用画布绘制贝塞尔曲线：

相关阅读

WPF如何绘制光滑连续贝塞尔曲线示例代码在三次贝塞尔曲线上找到点的切线JFreeChart简单实现光滑曲线绘制Java Swing：绘制曲线计算参数以定义二次贝塞尔曲线的分段

相关文章

贝尔算法面OpenCV索贝尔操作贝尔算法二面JavaFX曲线华为无线算法实习面试泡池子

相关问答

在画布中绘制曲线贝尔曼福特变奏曲使用PyQt5绘制多点曲线片段着色器-绘制曲线用Python绘制Bezier曲线的问题

相关工具

实时更新的曲线图尺子绘制Python QQopen-qqvue-qq

相关文档

手机 QQ 通用 API 文档Redis 设计与实现如何实现自己的 jQuery常用算法实现方法机器学习算法 Python 实现
快捷导航： 新手教程 算法原理 架构设计 Java进阶 数据库进阶 大厂专栏 面试经验 编程笔记 编程问答 所有专题 文档资料 工具软件 电子书籍 小牛导航
在线工具： 房贷计算器 个税计算器 Linux命令查询 Json格式化 正则表达式 颜色转换 AES加解密 SHA1加密 MD5加密 毒鸡汤 字数统计 随机密码生成 进制转换 Base64编解码 励志句子
Copyright © 2019-2024 小牛知识库@xnip.cn. All Rights Reserved.