JFreeChart简单实现光滑曲线绘制

用JFreeChart绘制光滑曲线，利用最小二乘法数学原理计算，供大家参考，具体内容如下

绘制图形：

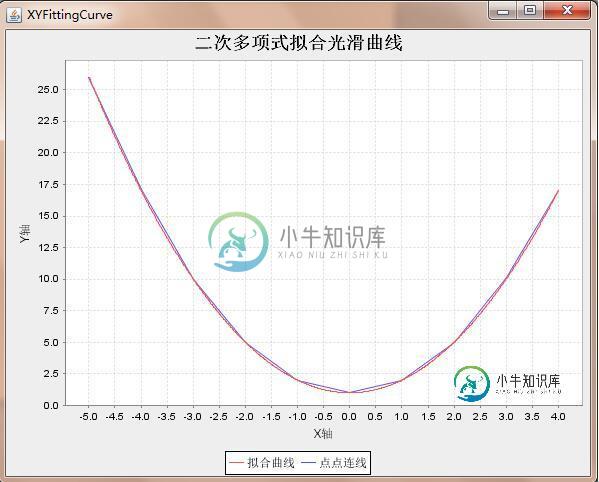
代码：

FittingCurve.java

package org.jevy; 
import java.util.ArrayList; 
import java.util.List; 
import org.jfree.chart.ChartFactory; 
import org.jfree.chart.ChartPanel; 
import org.jfree.chart.JFreeChart; 
import org.jfree.chart.axis.ValueAxis; 
import org.jfree.chart.plot.PlotOrientation; 
import org.jfree.chart.plot.XYPlot; 
import org.jfree.chart.renderer.xy.XYItemRenderer; 
import org.jfree.chart.renderer.xy.XYLineAndShapeRenderer; 
import org.jfree.data.xy.XYDataset; 
import org.jfree.data.xy.XYSeries; 
import org.jfree.data.xy.XYSeriesCollection; 
import org.jfree.ui.ApplicationFrame; 
import org.jfree.ui.RefineryUtilities; 
public class FittingCurve extends ApplicationFrame{ 
 List<Double> equation = null; 
 //设置多项式的次数 
 int times = 2; 
 
 public FittingCurve(String title) { 
 super(title); 
 //使用最小二乘法计算拟合多项式中各项前的系数。 
/* 
请注意： 多项式曲线参数计算 与 Chart图表生成 是分开处理的。 
多项式曲线参数计算： 负责计算多项式系数， 返回多项式系数List。 
Chart图表生成： 仅仅负责按照给定的数据绘图。 比如对给定的点进行连线。 
  本实例中，光滑的曲线是用密度很高的点连线绘制出来的。 由于我们计算出了多项式的系数，所以我们让X轴数据按照很小的步长增大，针对每一个X值，使用多项式计算出Y值， 从而得出点众多的(x,y)组。 把这些(x, y)组成的点连线绘制出来，则显示出光滑的曲线。 
XYSeries为JFreeChart绘图数据集， 用于绘制一组有关系的数据。 XYSeries对应于X,Y坐标轴数据集， 添加数据方式为： XYSeries s.add(x,y); 
XYSeriesCollection 为XYSeries的集合， 当需要在一个Chart上绘制多条曲线的时候，需要把多条曲线对应的XYSeries添加到XYSeriesCollection 
 添加方法：dataset.addSeries(s1); 
dataset.addSeries(s2); 
*/ 
 //多项式的次数从高到低，该函数需要的参数：x轴数据<List>，y轴数据<List>，多项式的次数<2> 
 this.equation = this.getCurveEquation(this.getData().get(0),this.getData().get(1),this.times); 
 
//生成Chart 
 JFreeChart chart = this.getChart(); 
 ChartPanel chartPanel = new ChartPanel(chart); 
 chartPanel.setPreferredSize(new java.awt.Dimension(500, 270)); 
 chartPanel.setMouseZoomable(true, false); 
 setContentPane(chartPanel); 
 } 
 
 public static void main(String[] args) { 
 // TODO Auto-generated method stub 
 FittingCurve demo = new FittingCurve("XYFittingCurve"); 
 demo.pack(); 
 RefineryUtilities.centerFrameOnScreen(demo); 
 demo.setVisible(true); 
 
 } 
 
 //生成chart 
public JFreeChart getChart(){ 
 //获取X和Y轴数据集 
 XYDataset xydataset = this.getXYDataset(); 
 //创建用坐标表示的折线图 
 JFreeChart xyChart = ChartFactory.createXYLineChart( 
 "二次多项式拟合光滑曲线", "X轴", "Y轴", xydataset, PlotOrientation.VERTICAL, true, true, false); 
 //生成坐标点点的形状 
 XYPlot plot = (XYPlot) xyChart.getPlot(); 
 
 XYItemRenderer r = plot.getRenderer(); 
 if (r instanceof XYLineAndShapeRenderer) { 
  XYLineAndShapeRenderer renderer = (XYLineAndShapeRenderer) r; 
  renderer.setBaseShapesVisible(false);//坐标点的形状是否可见 
  renderer.setBaseShapesFilled(false); 
  } 
 ValueAxis yAxis = plot.getRangeAxis(); 
 yAxis.setLowerMargin(2); 
 return xyChart; 
 } 
 
//数据集按照逻辑关系添加到对应的集合 
 public XYDataset getXYDataset() { 
 //预设数据点数据集 
 XYSeries s2 = new XYSeries("点点连线"); 
 for(int i=0; i<data.get(0).size(); i++){ 
 s2.add(data.get(0).get(i),data.get(1).get(i)); 
 } 
// 拟合曲线绘制 数据集 XYSeries s1 = new XYSeries("拟合曲线"); 
 //获取拟合多项式系数，equation在构造方法中已经实例化 
 List<Double> list = this.equation; 
 //获取预设的点数据 
 List<List<Double>> data = this.getData(); 
 
 //get Max and Min of x; 
 List<Double> xList = data.get(0); 
 double max =this.getMax(xList); 
 double min = this.getMin(xList); 
 double step = max - min; 
 double x = min; 
 double step2 = step/800.0; 
 //按照多项式的形式 还原多项式，并利用多项式计算给定x时y的值 
 for(int i=0; i<800; i++){ 
 x = x + step2; 
 int num = list.size()-1; 
 double temp = 0.0; 
 for(int j=0; j<list.size(); j++){ 
 temp = temp + Math.pow(x, (num-j))*list.get(j); 
 } 
 s1.add(x, temp); 
 } 
 
 //把预设数据集合拟合数据集添加到XYSeriesCollection 
 XYSeriesCollection dataset = new XYSeriesCollection(); 
 dataset.addSeries(s1); 
 dataset.addSeries(s2); 
 return dataset; 
 
 } 
 //模拟设置绘图数据（点） 
 public List<List<Double>> getData(){ 
 //x为x轴坐标 
 List<Double> x = new ArrayList<Double>(); 
 List<Double> y = new ArrayList<Double>(); 
 for(int i=0; i<10; i++){ 
 x.add(-5.0+i); 
 } 
 y.add(26.0); 
 y.add(17.1); 
 y.add(10.01); 
 y.add(5.0); 
 y.add(2.01); 
 
 y.add(1.0); 
 
 y.add(2.0); 
 y.add(5.01); 
 y.add(10.1); 
 y.add(17.001); 
 
 List<List<Double>> list = new ArrayList<List<Double>>(); 
 list.add(x); 
 list.add(y); 
 return list; 
 
 } 
 
//以下代码为最小二乘法计算多项式系数 
//最小二乘法多项式拟合 
 public List<Double> getCurveEquation(List<Double> x, List<Double> y, int m){ 
 if(x.size() != y.size() || x.size() <= m+1){ 
 return new ArrayList<Double>(); 
 } 
 List<Double> result = new ArrayList<Double>(); 
 List<Double> S = new ArrayList<Double>(); 
 List<Double> T = new ArrayList<Double>(); 
 //计算S0 S1 …… S2m 
 for(int i=0; i<=2*m; i++){ 
 double si = 0.0; 
 for(double xx:x){ 
 si = si + Math.pow(xx, i); 
 } 
 S.add(si); 
 } 
 //计算T0 T1 …… Tm 
 for(int j=0; j<=m; j++){ 
 double ti = 0.0; 
 for(int k=0; k<y.size(); k++){ 
 ti = ti + y.get(k)*Math.pow(x.get(k), j); 
 } 
 T.add(ti); 
 } 
 
 //把S和T 放入二维数组，作为矩阵 
 double[][] matrix = new double[m+1][m+2]; 
 for(int k=0; k<m+1; k++){ 
 double[] matrixi = matrix[k]; 
 for(int q=0; q<m+1; q++){ 
 matrixi[q] = S.get(k+q); 
 } 
 matrixi[m+1] = T.get(k); 
 } 
 for(int p=0; p<matrix.length; p++){ 
 for(int pp=0; pp<matrix[p].length; pp++){ 
 System.out.print(" matrix["+p+"]["+pp+"]="+matrix[p][pp]); 
 } 
 System.out.println(); 
 } 
 //把矩阵转化为三角矩阵 
 matrix = this.matrixConvert(matrix); 
 //计算多项式系数，多项式从高到低排列 
 result = this.MatrixCalcu(matrix); 
 return result; 
 } 
 //矩阵转换为三角矩阵 
 public double[][] matrixConvert(double[][] d){ 
 for(int i=0; i<d.length-1; i++){ 
 double[] dd1 = d[i]; 
 double num1 = dd1[i]; 
 
 for(int j=i; j<d.length-1;j++ ){ 
 double[] dd2 = d[j+1]; 
 double num2 = dd2[i]; 
 
 for(int k=0; k<dd2.length; k++){ 
 dd2[k] = (dd2[k]*num1 - dd1[k]*num2); 
 } 
 } 
 } 
 for(int ii=0; ii<d.length; ii++){ 
 for(int kk=0; kk<d[ii].length; kk++) 
 System.out.print(d[ii][kk]+" "); 
 System.out.println(); 
 } 
 return d; 
 } 
 
 //计算一元多次方程前面的系数， 其排列为 xm xm-1 …… x0（多项式次数从高到低排列） 
 public List<Double> MatrixCalcu(double[][] d){ 
 
 int i = d.length -1; 
 int j = d[0].length -1; 
 List<Double> list = new ArrayList<Double>(); 
 double res = d[i][j]/d[i][j-1]; 
 list.add(res); 
 
 for(int k=i-1; k>=0; k--){ 
 double num = d[k][j]; 
 for(int q=j-1; q>k; q--){ 
 num = num - d[k][q]*list.get(j-1-q); 
 } 
 res = num/d[k][k]; 
 list.add(res); 
 } 
 return list; 
 } 
 
 //获取List中Double数据的最大最小值 
 public double getMax(List<Double> data){ 
 double res = data.get(0); 
 for(int i=0; i<data.size()-1; i++){ 
 if(res<data.get(i+1)){ 
 res = data.get(i+1); 
 } 
 } 
 return res; 
 } 
 public double getMin(List<Double> data){ 
 double res = data.get(0); 
 for(int i=0; i<data.size()-1; i++){ 
 if(res>data.get(i+1)){ 
 res = data.get(i+1); 
 } 
 } 
 return res; 
 } 
 
} 

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。