6.3 基于归纳的知识图谱推理
随着技术的发展，越来越多的知识图谱自动化构建方法被提出来，例如利用算法对文本进行三元组抽取，这使得大规模知识图谱能够迅速被建立起来，例如 NELL。但这类知识图谱的信息准确度稍差于利用专家知识人工构建的知识图谱，且冗余度较大。在这种自动化构建的大规模知识图谱上进行推理，知识的不精确性以及巨大的规模对演绎推理来说是很大的挑战，而归纳推理却很适用。
基于归纳的知识图谱推理主要是通过对知识图谱已有信息的分析和挖掘进行推理的，最常用的信息为已有的三元组。按照推理要素的不同，基于归纳的知识图谱推理可以分为以下几类：基于图结构的推理、基于规则学习的推理和基于表示学习的推理。下面分别介绍这三类推理的主要方法和现有进展。
6.3.1 基于图结构的推理
1.方法概述
对于那些自底向上构建的知识图谱，图谱中大部分信息都是表示两个实体之间拥有某种关系的事实三元组。对于这些三元组，从图的角度来看，可以看作是标签的有向图，有向图以实体为节点，以关系为有向边，并且每个关系边从头实体的节点指向尾实体的节点，如图6-11所示。
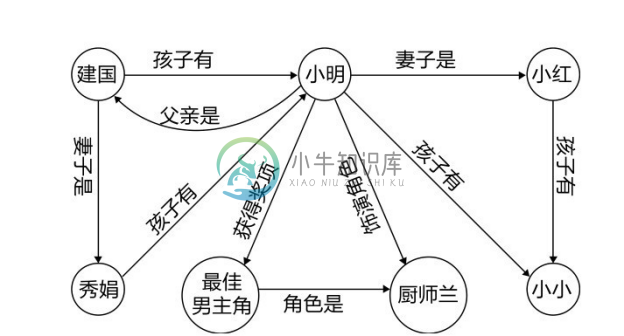
图6-11 知识图谱中的实体关系图
有向图中丰富的图结构反映了知识图谱丰富的语义信息，在知识图谱中典型的图结构是两个实体之间的路径。例如，上面的示例中描述了不同人物之间的关系以及人物的职业信息，包含了如下的路径：
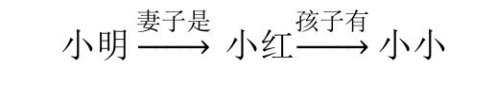
这是一条从实体小明到实体小小的路径，表述的信息是小明的妻子是小红，小红的孩子有小小。从语义角度来看，这条由关系“妻子是”和“孩子有”组成的路径揭示了小明和小小之间的父子关系，这条路径蕴涵着三元组：
而这个推理过程不仅仅存在于这个包含小明、小红和小小的子图中，同样也存在于建国、秀娟和小明的子图中，而路径
和三元组
是常常同时出现在知识图谱中的。其中 A、B、C 是三个代表关系的变量，由“妻子是”和“孩子有”两种关系组成的路径与关系“孩子有”在图谱中是经常共现的，且其共现与 A、B、C 具体是什么实体没有关系。这说明了路径是一种重要的进行关系推理的信息，也是一种重要的图结构。除了路径，实体的邻居节点以及它们之间的关系也是刻画和描述一个实体的重要信息，例如在上例中的关于“小明”的7个三元组鲜明地描述了小明这个人物，包括（小明，父亲是，建国）、（小明，获得奖项，最佳男主角）以及（小明，妻子是，小红）等。一般而言，离实体越近的节点对描述这个实体的贡献越大，在知识图谱推理的研究中，常考虑的是实体一跳和两跳范围内的节点和关系。
当把知识图谱看作是有向图时，往往强调的是在知识图谱中的事实三元组，即表示两个实体之间拥有某种关系的三元组，而对于知识图谱的本体和上层的 schema 则关注较少，因为本体中许多含有丰富逻辑描述的信息并不能简单地转化为图的结构。下面将介绍常见的基于图结构的知识图谱推理算法。
2.常见算法简介
典型的基于图结构的推理方法有PRA（Path Ranking Algorithm）[10] 利用了实体节点之间的路径当作特征从而进行链接预测推理。
（1）基于知识图谱路径特征的 PRA 算法。PRA 处理的推理问题是关系推理，其中包含了两个任务，一个是给定关系r和头实体h预测可能的尾实体t是什么，即在给定h,r的情况下，预测哪个三元组（h,r,t）成立的可能性比较大，叫作尾实体链接预测；另一个是在给定r,t的情况下，预测可能的头实体h是什么，叫作头实体链接预测。
PRA 针对的知识图谱主要是自底向上自动化构建的含有较多噪声的图谱，例如NELL，并将关系推理的问题形式化为一个排序问题，对每个关系的头实体预测和尾实体预测都单独训练一条排序模型。PRA 将存在于知识图谱中的路径当作特征，并通过图上的计算对每个路径赋予相应的特征值，然后利用这些特征学习一个逻辑斯蒂回归分类器完成关系推理。在 PRA 中，每一个路径可以当作对当前关系判断的一个专家，不同的路径从不同的角度说明了当前关系的存在与否。
在PRA中，利用随机游走的路径排序算法首先需要生成一些路径特征，一个路径P是由一系列关系组成的，即：
式中，Tn 为关系rn 的作用域（range)以及关系rn−1 的值域（domian)，即Tn =range（rn ）=domain（rn−1 ），关系的值域和作用域通常指的是实体的类型。基于路径的随机游走定义了一个关系路径的分布，并得到每条路径的特征值sℎ,P（t） ,sℎ,P（t） 可以理解为沿着路径P从h开始能够到达t的概率。具体操作为，在随机游走的初始阶段，sℎ,P（e） 初始化为1，如果e=s，否则初始化为0。在随机游走的过程中，sℎ,P（e） 的更新原则如下：
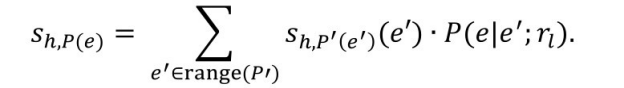
式中
表示从节点e′ 出发沿着关系rl 通过一步的游走能够到达节点e的概率。对于关系r，在通过随机游走得到一系列路径特征Pr ={P1 ,⋯, Pn }之后，PRA 利用这些路径特征为关系r训练一个线性的预测实体排序模型，其中关系r下的每个训练样本，即一个头实体和尾实体的组合的得分计算方法如下：
基于每个样本的得分，通过一个逻辑斯蒂函数得到每个样本的概率，即：
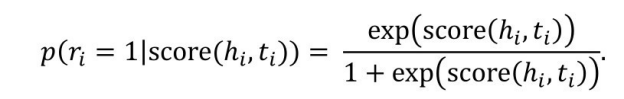
再通过一个线性变化加上最大似然估计，设计损失函数如下：
li （θ）= wi [yi ln pi +（1− yi ）ln（1−pi ）].
式中，yi 为训练样本（hi ,ti ）是否具有关系r的标记，如果（hi ,r,ti ）存在，则标记为1；如果不存在，则标记为0。
在路径特征搜索的过程中，PRA 增加了对有效路径特征的约束，来有效减小搜索空间：路径在图谱中的支持度（support）应大于某设定的比例α； 路径的长度小于或等于某设定的长度；每条路径至少有一个正样本在训练集中。采集路径随机游走过程采用了 LVS （Low-Variance Sampling）的方法。
结合了有效采样和随机有走的 PRA 能够快速有效地利用知识图谱的路径结构对知识图谱进行关系推理，是典型的基于图结构的知识图谱推理算法。
（2）PRA 的演化算法。在 PRA 中的路径是连续的且在路径中的关系是同向的，这种路径特征可以理解为一种简单的霍恩规则（Horn rule），但是在知识图谱中，有很多种路径是含有常量的：
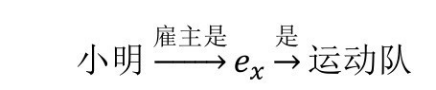
由这个路径可以推理出三元组小明
，这种有明显语义的含有常量的且不是收尾闭合的路径特征是不能被 PRA 捕捉到的，又例如由t=NFL直接推理ex 
，即将 NFL 直接设置为关系“服役于运动队”的值域，这种很明显的推理特征也是 PRA 无法捕捉的。所以，CoR-PRA（Constant and Reversed Path Ranking Algorithm）[43] 通过改变 PRA 的路径特征搜索策略，促使其能够涵盖更多种语义信息的特征，主要是包含常量的图结构特征。给定关系 r 下的训练样本（h,t）,Co-PRA 中搜索图结构特征的步骤如下：
1）生成初步的路径。通过路径搜索算法生成以h为起点的小于长度l的路径集合Pℎ ；通过路径搜索算法生成以t为起点的小于长度l的路径集合Pt 。
2）通过 PRA 计算路径特征的概率。对于路径πℎ ∈Pℎ ， 计算沿着路径πℎ 正向地由h到达x的概率P（h→x; πℎ ），以及沿着路径πℎ 逆向地由h到达x的概率
；同理，对路径πt ∈Pt ，计算沿着路径πt 正向地由t到达x的概率P（t→x; πt ），以及沿着路径πt 逆向地由t到达x的概率
；并将所有的x放入常量候选集N中。
3）生成候选的常量路径。对每一个（x∈N,πϵPt ）的组合，如果P（t→x| πt ）＞0，那么生成路径特征
，其中c=x，并且将路径特征对应的覆盖度值（coverage）加1，即
；同理，对每一个（x∈N,πϵPt ）的组合，如果
，那么生成路径特征P（c→t; πt ），其中c=x，并且将路径特征对应的覆盖度值加1，即coverage（P（c→t; πt ））+=1。
4）生成更长的路径特征候选集（Long Concatenated Path Candidates）。对每一个可能的组合（x ∈N,πℎ ∈Pℎ , πt ∈Pt ），如果P（s←x |πs ）＞0 且
，就生成路径
并且更新其覆盖度，即
，同时更新其准确度，即
。反向同理。
从路径搜索过程可以看出，相比 PRA,CoR-PRA 最重要的不同有两方面，一是增加了带有常量的路径特征的搜索，二是搜索过程由单项搜索变成了双向搜索。
尽管采用了随机游走策略来降低搜索空间，当 PRA 应用在关系丰富且连接稠密的知识图谱上时，依然会面临路径特征爆炸的问题。为了提高 PRA 的路径搜索效率以及路径特征的丰富度，Gardner[44] 提出了 SFE（Subgraph Feature Extraction）模型，改变了 PRA的路径特征搜索过程。为了提升路径搜索的效率，SFE 去除了路径特征的概率计算这个需要较大计算量的过程，而是直接保留二值特征，仅记录此路径是否在两个实体之间存在， SFE 首先通过随机游走采集每个实体的制定步数以内的子图特征，并记录下子图中所有的结束节点实体e，对于某个关系的训练样本实体对（h,t），如果实体ei 同时存在于实体h和t的结束实体集中，那么就以ei 为链接节点，将h和t对应子图中的结构生成一条h和t之间的路径。为了进一步提升路径搜索效率，降低无意义的路径特征，对于图中的一个节点，如果这个节点有很多相同关系边ri 连接着不同的实体节点，那么沿着这个关系继续搜索路径会急剧增加子图大小的量级。为了进一步提升搜索效率，在 SFE 中，这个关系ri 将不会作为当前深度优先搜索路径中的一个关系，从而停止搜索，并把当前节点当作实体子图中的一个结束节点。为了增加子图特征的丰富性，除了 PRA 中用到的路径特征，SFE 还增加了二元路径特征，类似自然语言处理中的bigram，即将两个具有连接的关系组成一个新的关系，例如“BIGRAM：对齐实体/妻子是”，除了二元路径特征，SFE 还增加了 one-sided feature,one-sided path 指的是一个存在在给定两个节点之间的路径的，是从起始节点开始，但不一定由另一个节点结束，类似Co-PRA中的带有常量的路径特征。SFE还会对给定的两个节点进行one-sided feature的比较，如果两个节点都具有相同的关系ri ，例如“性别是”，那么将会把两个节点的ri 以及连接的实体记录下来。如果两个节点在关系ri 下连接的节点是一样的，那么这个特征是可以被 PRA 路径特征捕捉到的，但是如果取值不一样就只有 SFE 能捕捉到。SFE 同时还利用了关系的向量表示，通过训练好的关系的表示，将已有路径特征中的关系替换为向量空间中比较相似的关系。SFE 还增加了一个表示任意关系的关系ANYREL来增加路径特征的丰富性。总体来说，SFE在PRA的路径特征搜索的效率和特征的丰富性方面做了比较大的提升。
从基于图结构的 PRA 系列研究可以看出，被研究得比较多的图结构是与路径相关的结构特征，在利用路径特征的过程中，一个重要的问题是如何有效地搜索到路径，涌现出了很多提升路径搜索效率的研究工作。但路径相关的特征还不能覆盖知识图谱中包含的所有语义信息，因而由相关工作通过引入带有实例的路径来丰富图特征所包含的语义信息的类型。但是，不是路径形式的图结构特征依然有待挖掘和分析。
2.典型工具简介或实验对比分析
PRA的提出主要是针对很不完整的知识图谱，所以论文中的实验是在知识图谱NELL上进行试验的，图6-12展示了PRA中在预测某一关系时权重最高的两个路径特征，可以看出，这些高权重的路径特征可以看作是预测当前关系的一条置信度较高的规则，具有明显的语义含义。
PRA在链接预测上与N-FOIL的对比结果如图6-13所示，从结果中可以看出，p@10方面PRA和N-FOIL效果差不多，但是在p@100和p@1000方面，PRA的结果明显优于N-FOIL。
图6-12 PRA关系预测路径
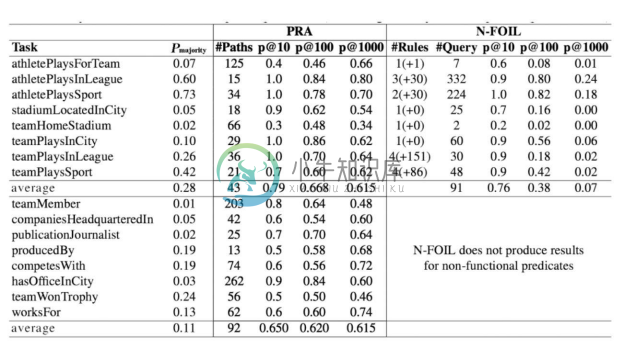
图6-13 PRA在链接预测上与N-FOIL的对比结果
图6-14展示了CoR-PRA在知识图谱推理和命名实体抽取上的实验比较，从实验结果可以看出，CoR-PRA 由于提升了路径特征的丰富性，其结果明显优于 PRA，但计算效率不及PRA。
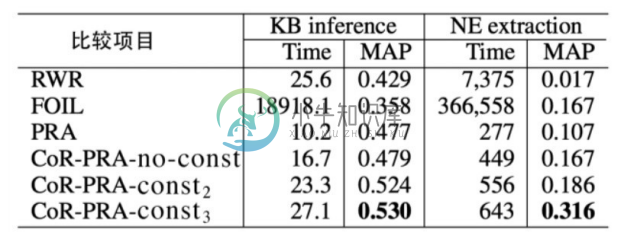
图6-14 知识图谱推理及命名实体抽取结果对比
图6-15展示了SFE和PRA的性能比较，左边是在同样的拥有10个关系的NELL数据集上PRA和SFE的 MAP（Mean Average Precision）结果、平均抽取的特征数量以及运行时间的比较。从实验预测结果来看，用深度优先搜索策略（BFS）代替了随机游走（RW）的 SFE 表现最好，并且能够抽取到更多样的特征，且总耗时更短，效率提升明显。
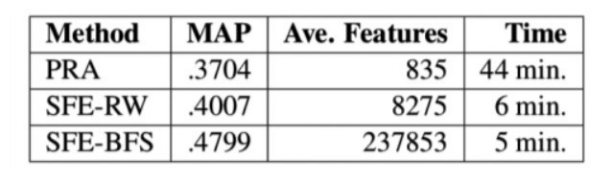
图6-15 SFE和PRA的性能比较
典型的 PRA 系列工具可以参考 https://github.com/noon99jaki/pra，集成了 PRA 以及CoR-PRA算法。
6.3.2 基于规则学习的推理
1.方法概述
基于规则的推理具有精确且可解释的特性，规则在学术界和工业界的推理场景都有重要的应用。规则是基于规则推理的核心，所以规则获取是一个重要的任务。在小型的领域知识图谱上，规则可以由领域专家提供，但在大型、综合的知识图谱方面，人工提供规则的效率比较低，且很难做到全面和准确。所以，自动化的规则学习方法应运而生，旨在快速有效地从大规模知识图谱上学习置信度较高的规则，并服务于关系推理任务。
规则一般包含了两个部分，分别为规则头（head）和规则主体（body），其一般形式为
rule: head ←body.
解读为有规则主体的信息可推出规则头的信息。其中，规则头由一个二元的原子（atom）构成，而规则主体由一个或多个一元原子或二元原子组成。原子（atom）是指包含了变量的元组，例如 isLocation(X)是一个一元原子表示实体变量 X 是一个位置实体；hasWife(X, Y)是一个二元原子，表示实体变量X的妻子是实体变量Y。二元原子可以包含两个或一个，例如liveIn(X, Hangzhou)是一个指含有一个实体变量X的二元原子，表示了变量 X 居住在杭州。在规则主体中，不同的原子是通过逻辑合取组合在一起的，且规则主体中的原子可以以肯定或否定的形式出现，例如如下规则：
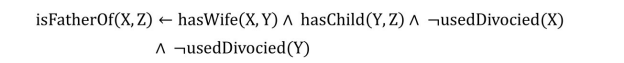
这里的规则示例说明了如果任意实体X的妻子是实体Y，且实体Y的孩子有Z且X和 Y 都不曾离婚，那么可以推出 X 的孩子也有 Z。这条规则里的规则主体就包含了以否定形式出现的原子。所以，规则也可以表示为：
rule: head ←body+ ∧body− .
其中，body+ 表示以肯定形式出现的原子的逻辑合取集合，而body− 表示以否定形式出现的原子的逻辑合取集合。如果规则主体中只包含有肯定形式出现的原子而不包含否定形式出现的原子，称这样的规则为霍恩规则（horn rules），霍恩规则是被研究得比较多的规则类型，可以表示为以下形式：
a0 ← a1 ∧a2 ∧… ∧an .
其中，每个ai 都为一个原子。在知识图谱的规则学习方法中，另一种被研究得比较多的规则类型叫作路径规则（path rules），路径规则可以表示为如下形式：
r0 （e1 ,en+1 ）← r1 （e1 ,e2 ）∧r2 （e2 ,e3 ）∧… ∧rn （en ,en+1 ）.
其中，规则主体中的原子均为含有两个变量的二元原子，且规则主体的所有二元原子构成一个从规则头中的两个实体之间的路径，且整个规则在知识图谱中构成一个闭环结构。这几种不同规则的包含关系如下：
路径规则 ∈霍恩规则 ∈一般规则.
即路径规则是霍恩规则的一个子集，而霍恩规则又是一般规则的一个子集，从规则的表达能力来看，一般规则的表达能力最强，包含各种不同的规则类型，而霍恩规则次之，规则路径的表达能力最弱，只能表达特定类型的规则。
在规则学习过程中，对于学习到的规则一般有三种评估方法，分别是支持度（support）、置信度（confidence）、规则头覆盖度（head coverage）。下面分别介绍这三种评价指标的计算方法。
对于一个规则rule，在知识图谱中，其支持度（support）指的是满足规则主体和规则头的实例个数，规则的实例化指的是将规则中的变量替换成知识图谱中真实的实体后的结果。所以，规则的支持度通常是一个大于或等于0的整数值，用 support(rule)表示。一般来说，一个规则的支持度越大，说明这个规则的实例在知识图谱中存在得越多，从统计角度来看，也越可能是一个比较好的规则。
规则的置信度（confidence）的计算方式为：
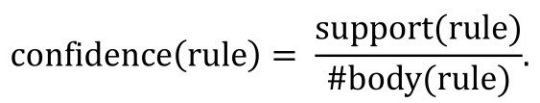
即规则支持度和满足规则主体的实例个数的比值，即在满足规则主体的实例中，同时也能满足规则头的实例比例。一个规则的置信度越高，一般说明规则的质量也越高。由于知识图谱往往具有明显的不完整性，而前文介绍的规则置信度计算方法间接假设了不存在知识图谱中的三元组是错误的，这显然是不合理的。所以，基于部分完全假设（Partial Completeness Assumption,PCA）的置信度（PCA Confidence）也是一个衡量规则质量的方法，且考虑了知识图谱的不完整性。PCA置信度的计算方法为
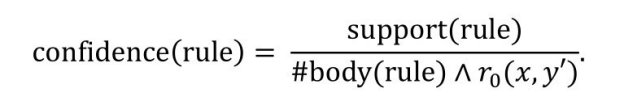
从上面的式子可以看出，和前文介绍的置信度计算方法相比，PCA 置信度最大的区别是分母中需要多考虑一个条件r0 （x,y′），这里r0 （x,y）是规则头，而r0 （x,y′）说明在知识图谱中，只要当规则头中的头实体x通过关系r0 连接到除y以外的实体时才能算进分母的计数，否则不作分母计数。这样考虑的原因是，如果头实体x和关系r0 没有在知识图谱中构成相关的三元组，而通过规则主体可以推出三元组r0 （x,y），那么根据知识图谱的不完全假设，r0 （x,y）只是在知识图谱中缺失而不是错误的三元组，所以，不应该将这类实例化例子计算在分母中，否则会降低规则的置信度。所以，在 PCA 置信度中排除了来自这类实例对置信度值的负向影响。
规则头覆盖度（Head Coverage）的计算方法为
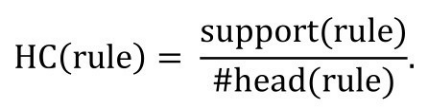
即规则支持度和满足规则头的实例个数的比值，即在满足规则头的实例中，同时也满足规则主体的实例比例。一个规则的置信度越高，一般说明规则的质量也越高。
规则的支持度、置信度以及头覆盖度从不同的角度反映了规则的质量，但三者之间没有必然的关联关系。例如，置信度高的规则，其头覆盖度并不一定高，所以在规则学习中通常会结合这三个评价指标综合衡量规则的质量。
2.常见算法简介
下面介绍具体的规则学习方法，首先介绍典型的规则学习方法 AMIE[12] 。AMIE 能挖掘的规则形如：
father Of（f,c）←motherOf（m,c）∧marriedTo（m,f）.
AMIE 是一种霍恩规则，也是一种闭环规则，即整条规则可以在图中构成一个闭环结构。在规则学习的任务中，最重要的是如何有效搜索空间，因为在大型的知识图谱上简单地遍历所有可能的规则并评估规则的质量效率很低，几乎不可行。AMIE 定义了3个挖掘算子（Mining Operators），通过不断在规则中增加挖掘算子来探索图上的搜索空间，并且融入了对应的剪枝策略。3个挖掘算子如下：
●增加悬挂原子（Adding Dangling Atom）。即在规则中增加一个原子，这个原子包含一个新的变量和一个已经在规则中出现的元素，可以是出现过的变量，也可以是出现过的实体。
●增加实例化的原子（Adding Instantiated Atom）。即在规则中增加一个原子，这个原子包含一个实例化的实体以及一个已经在规则中出现的元素。
●增加闭合原子（Adding Closing Atom）。即在规则中增加一个原子，这个原子包含的两个元素都是已经出现在规则中的变量或实体。增加闭合原子之后，规则就算构建完成了。
AMIE的规则学习算法如图6-16所示。
图6-16 AMIE的规则学习算法
在探索规则结构的过程中，AMIE 还引入了两个重要的剪枝策略，来有效缩小搜索空间。AMIE的剪枝策略主要包含两条：
●设置最低规则头覆盖度过滤，头覆盖度很低的规则一般是一些边缘规则，可以直接过滤掉。在实践中，AMIE将头覆盖度值设为0.01。
●在一条规则中，每在规则主体中增加一个原子，都应该使得规则的置信度增加，即confidence（a0 ←a0 ∧a2 ∧…∧an ∧an+1 ）＞confidence（a0 ←a0 ∧a2 ∧…∧an ）。如果在规则中增加一个新的原子an+1 ，但没有提升规则整体的置信度，那么就将拓展后的规则a0 ←a0 ∧a2 ∧…∧an ∧an+1 剪枝掉。
在规则学习过程中，AMIE 通过 SPARQL 在知识图谱上的查询对规则的质量进行评估。无论采用哪种挖掘算子来增加规则中的原子，每一个原子都伴随着需要选择一个知识图谱中的关系。在选择增加实例化算子时还涉及选择一个实体方面，为了满足选出来的实体和关系组成的原子，在添加到规则中以后，能够满足事先设置的头覆盖度的要求， AMIE用对知识图谱的查询来筛选合适的选项，例如：
SELECT ?r WHERE a0 ∧a1 ∧… ∧an ∧?r（X,Y）
HAVVING COUNT（a0 ）≥k
这样经过查询筛选得到的关系候选项满足了一定符合头覆盖度的要求。
3.典型工具简介
图6-17展示了 AMIE 在不同数据集上的运行效果，从中可以看出 AMIE 在大规模知识图谱上的效率较高。例如，在拥有100多万个实体以及近700万个三元组的 DBpedia上，AMIE 仅需不到3min 就能完成规则挖掘，产生7000条规则，并帮助推理出了12万多个新的三元组。
图6-17 AMIE不同数据集规则挖掘结果对比
规则挖掘的典型工具 AMIE 可参考 http://www.mpi-inf.mpg.de/departments/ontologies/projects/amie/，其中包括了进一步提升AMIE效率的AMIE+[45] 。
6.3.3 基于表示学习的推理
1.方法概述
基于图结构的推理和基于规则学习的推理，都显式地定义了推理学习所需的特征，而基于表示学习的推理通过将知识图谱中包括实体和关系的元素映射到一个连续的向量空间中，为每个元素学习在向量空间中表示，向量空间中的表示可以是一个或多个向量或矩阵。表示学习让算法在学习向量表示的过程中自动捕捉、推理所需的特征，通过训练学习，将知识图谱中离散符号表示的信息编码在不同的向量空间表示中，使得知识图谱的推理能够通过预设的向量空间表示之间的计算自动实现，不需要显式的推理步骤。
知识图谱的表示学习受自然语言处理关于词向量研究的启发，因为在 word2vec 的结果中发现了一些词向量具有空间平移性，例如：
vec（king）− vec（queen）≈vec（man）− vec（woman）
即“king”的词向量减去“queen”的词向量的结果约等于“man”的词向量减去“woman”的词向量的结果，这说明“king”和“queen”在语义上的关系与“man”和“woman”之间的关系比较近似。而拓展到知识图谱上，就可以理解为拥有同一种关系的头实体和尾实体对，在向量空间的表示可能具有平移不变性，这启发了经典的知识图谱表示学习方法TransE的提出以及知识图谱表示学习的相关研究。
2.常见算法简介
首先介绍最经典的 TransE[11] 模型，为了方便起见，将一个三元组表示成（h,r,t），其中h表示头实体（head entity）,r表示关系（relation），而t表示尾实体（tail entity）。在TransE 中，知识图谱中的每个实体和关系都被表示成了一个向量，按照词向量的启示， TransE 将三元组中的关系看作是从头实体向量到尾实体向量的翻译（translation），并对知识图谱将要映射到的向量空间做了如下假设，即在理想情况下，对每一个存在知识图谱中的三元组都满足
h+r=t.
式中，h是头实体的向量表示；r是关系的向量表示；t是尾实体的向量表示。TransE 假设在任意一个知识图谱中的三元组（h,r,t），头实体的向量表示h加上关系的向量表示r应该等于尾实体的向量表示t。在需要映射到的向量空间中，TransE 将关系看作是从头实体向量到尾实体向量的翻译，即头实体向量通过关系向量的翻译得到尾实体，则说明这个三元组在知识图谱中成立。等式h+r=t是一个理想情况的假设，根据这个假设，TransE 在训练阶段的目标是：
对正样本三元组： h+r≈t；
对负样本三元组： h+r≉t.
h+r和t之间的近似程度可以用向量相似度衡量，TransE 采用欧式计算两个向量的相似度，所以TransE的三元组得分函数设计为
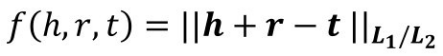
对于正样本三元组，得分函数值尽可能小；而对于负样本三元组，得分函数值尽可能大。然后通过一个正负样本之间最大间隔的损失函数，设计训练得到知识图谱的表示学习结果，其损失函数为
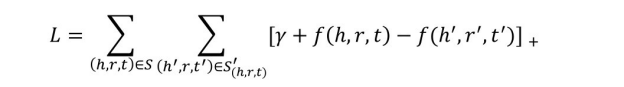
式中，S表示知识图谱中正样本的集合；S（′ℎ,r,t）表示（h,r,t）的负样本，在训练过程中三元组（h,r,t）的负样本通过随机替换头实体h或者尾实体t得到；[x]+ 表示max （0,x）;γ表示损失函数中的间隔，是一个需要设置的大于零的超参。TransE的训练目标是最小化损失函数L，可以通过基于梯度的优化算法进行优化求解，直至训练收敛。
实践证明，TransE由于其有效合理的向量空间假设，是一种简单高效的知识图谱表示学习方法，并且能够完成多种关系的链接预测任务。TransE的简单高效说明了知识图谱表示学习方法能够自动且很好地捕捉推理特征，无须人工设计，很适合在大规模复杂的知识图谱上推广，是一种有效的知识图谱推理手段。
尽管有效，TransE依然存在着表达能力不足的问题，例如按照关系头尾实体个数比例划分，知识图谱中的关系可以分为四种类型，分别为一对一（1-1）、一对多（1-N）、多对一（N-1）以及多对多（N-N）,TransE 能够较好地捕捉一对一（1-1）的关系，却无法很好地表示一对多（1-N）、多对一（N-1）以及多对多（N-N）的关系。例如，实体“中国”在关系“拥有省份”这个关系下有很多个尾实体，根据 TransE 的假设，任何一个省份的向量表示都满足v（省份x）: v（中国）+ v（拥有省份）= v（省份x），这将会导致 TransE无法很好地区分各个省份。所以，TransH[46] 就提出了在通过关系将头实体向量翻译到尾实体向量之前，先将头实体和尾实体向量投影到一个和当前关系相关的平面上，由于向量空间中的不同向量在同一个平面上的投影可以是一样的，这就帮助 TransE 从理论上解决了难以处理一对多（1-N）、多对一（N-1）以及多对多（N-N）关系的问题，TransE 和TransH的对比向量空间假设对比如图6-18所示。
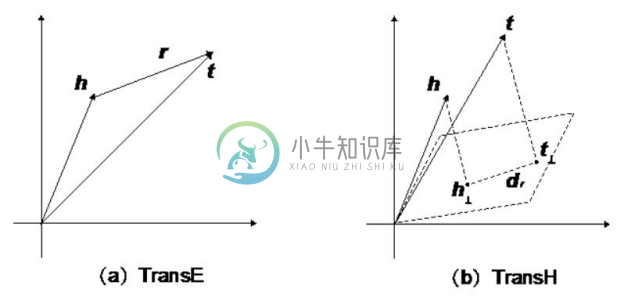
图6-18 TransE和TransH对比向量空间假设对比
TransH 为每个关系r都设计了一个投影平面，并用投影平面的法向量wr 表示这个平面，h和t的投影向量的计算方法如下：
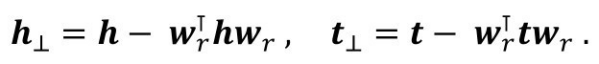
然后，利用投影向量进行三元组得分的计算，即
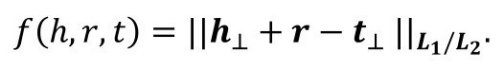
TransH 通过设计关系投影平面提升了 TransE 表达非一对一关系的能力，TransR[8] 则通过拆分实体向量表示空间和关系表示向量空间来提升 TransE 的表达能力。由于实体和关系在知识图谱中是完全不同的两种概念，理应表示在不同的向量空间而不是同一个向量空间中，所以TransR拆分了实体表示空间和关系表示空间，如图6-19所示。
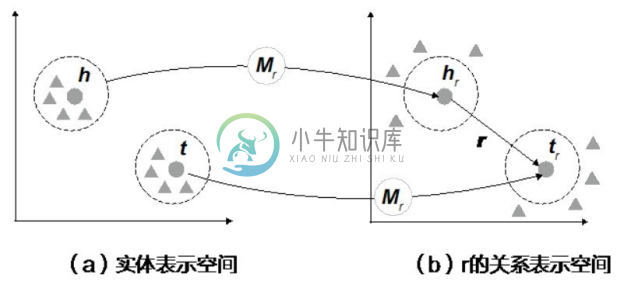
图6-19 TransR的实体表示空间和关系表示空间
TransR 设定所有的计算都发生在关系表示空间中，并在计算三元组得分之前首先将实体向量通过关系矩阵投影向关系表示空间，即：
hr =hMr , tr =tMr .
然后，利用投影到关系表示空间的头实体向量和尾实体向量进行三元组得分的计算：
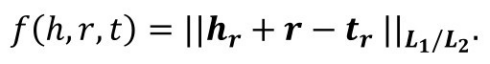
TransR 通过区分实体和关系表示空间增加了模型的表达能力，并提升了表示学习结果，但是在 TransR 中，每个关系除拥有一个表示向量以外，还对应了一个d × d的矩阵，这相比起 TransE 增加了很多参数。为了减少 TransR 的参数量且同时保留其表达能力， TransD[47] 提出了用一个与实体相关的向量以及一个与关系相关的向量通过外积计算，动态地得到关系投影矩阵，如图6-20所示。
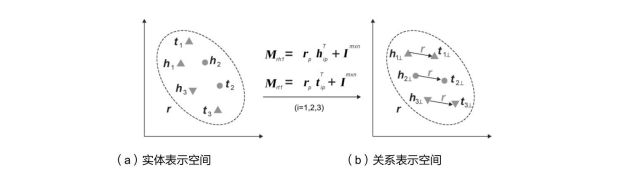
图6-20 TransD实体表示空间和关系表示空间
其动态矩阵的计算如下：
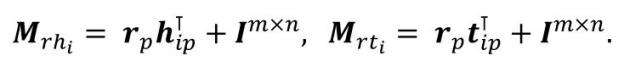
式中，m,n为关系和实体的向量表示维度；m,n可以相等也可以不相等。TransD 通过动态计算投影矩阵不仅可以显著减少关系数量较大且实体数量不多的知识图谱中的参数，而且增加了 TransD 捕捉全局特征的能力，使得其在链接预测任务上的表现比 TransR 更好。
之前介绍了以 TransE 为代表的基于翻译假设的表示学习模型，而知识图谱表示学习的推理能力和采用的向量空间假设有很大关系，除了翻译假设还有其他的空间假设， DistMult[48] 采用了更灵活的线性映射假设将实体表示为向量，关系表示为矩阵，并将关系当作是一种向量空间中的线性变换。对于一个正确的三元组（h,r,t），假设以下公式成立：
hMr =t.
式中，h和t分别为头实体和尾实体的向量表示；Mr 为关系r的矩阵表示。上式表达的意思是头实体通过与关系矩阵相乘，经过空间中的线性变化以后，可以转变为尾实体向量。所以，训练目标是对正确的三元组让hMr 与t尽可能接近，而错误的三元组尽可能远离。与 TransE 不同的是，DistMult 采用向量点积衡量两个向量接近与否，故三元组的得分函数设计如下：
f（h,r,t）= hMr t⊺ .
损失函数与 TransE 系列的方法相同，设计为基于最大间隔的损失函数。由于向量与矩阵的运算比向量的加法运算更灵活，所以整体来说 DistMult 的效果比 TransE 效果要好。当将关系的矩阵设计为对角矩阵时，参数量与 TransE 相同，且效果比普通矩阵更好。所以，在DistMult系列的方法中，常常将关系的表示设置为对角矩阵。
基于 TransE 有很多丰富表达能力的模型，而基于 DistMult 也有很多提升方法。DistMult 中一个比较明显的问题是，得分函数的设计使得当关系设计为对角矩阵时，无法隐含所有关系都是对称关系的结论，因为对于一个存在的三元组（h,r,t），经过模型训练以后，f（h,r,t）=hDr t⊺ 的值会比较大，即表示三元组（h,r,t）是正确的。所以，三元组（t,r,h）的得分f（t,r,h）= tDr h⊺ 的值也会比较大，因为tDr h⊺ = hDr t⊺ 。这说明了DistMult 天然地假设了所有的关系是对称关系，这显然是不合理的。从语义的角度分析，知识图谱中的关系既包含了对称关系如“配偶是”，也包含了不对称关系如“出生地”，而且非对称关系一般还多于对称关系。为了解决这个问题，ComplEx[49] 将原来基于实数的表示学习拓展到了复数，因为基于复数的乘法计算是不满足交换律的，从而克服了 DistMult不能很好地表示非对称关系的问题。其得分函数的计算如下：
f（h,r,t）= ＜Re（h）,Re（r）,Re（t）＞
+＜Re（h）,Im（r）,Im（t）＞
+＜Im（h）,Re（r）,Im（t）＞
−＜Im（h）,Im（r）,Im（t）＞
式中，Re（x）表示复数 x的实部，Im（x）表示x的虚部，＜x,y,z＞ =xyz。可以看出在ComplEx中，f（h,r,t）≠f（t,r,h），所以可以更灵活地表达对称与非对称关系。
类比推理是一种类型重要的推理类型，一个具有良好推理的知识图谱表示学习模型理应具有这种推理的能力，所以，ANALOGY[50] 对知识图谱中的类比推理的基本结构进行了分析，并通过在DistMult的学习过程增加两个对于关系矩阵表示的约束，来提升DistMult的模型的类比推理能力，使得模型的整体推理能力得到了提升。
除目前提到的表示学习方法，还有很多其他思路的表示学习方法，例如纯神经网络方法NTN[51] 、ConvE[52] 等，这里不再赘述。
3.典型工具简介或实验对比分析
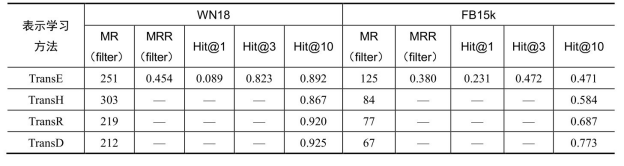
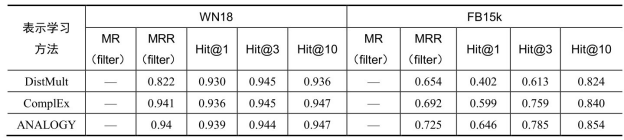
表6-6为常用知识图谱表示学习方法链接预测结果比较，采用的评价指标包括平均排序（Mean Rank,MR）、倒数平均排序（Mean Reciprocal Rank,MRR）以及排序n以内的占比(Hit@n)。从实验结果可以看出，整体来说线性变换假设模型的表现优于翻译模型系列。
表6-6 常用知识图谱表示学习方法链接预测结果比较
续表
常用的关于知识图谱表示学习的工具包有清华开源的 OpenKE，它涵盖了常见的表示学习模型，并有 PyTorch、TensorFlow 以及 C++版本。全面的关于工具包的信息可以在网站主页获得。