6.1 推理概述
6.1.1 什么是推理
推理在人类长期的社会发展和演变中扮演着重要的角色,包含了思考、认知和理解,是认知世界的重要途径。具体来说,推理是通过已有知识推断出未知知识的过程。推理的方法大致可以分为逻辑推理和非逻辑推理,其中逻辑推理的过程包含了严格的约束和推理过程,而非逻辑推理的过程相对模糊。逻辑推理由于其透明性,被广泛研究且定义比较清晰,所以本章讨论的推理主要也围绕逻辑推理展开。
逻辑推理按照推理方式的不同包含两大类:演绎推理(Deductive Reasoning)和归纳推理(Inductive Reasoning)。其中,归纳推理又包含了溯因推理(Abductive Reasoning)和类比推理(Analogy Reasoning)等。下面先介绍这四种基本的推理。
演绎推理[1] 是一种自上而下(top-down logic)的逻辑推理,是指在给定的一个或多个前提的情况下,推断出一个必然成立的结论的过程。典型的演绎推理有肯定前件假言推理、否定后件假言推理(Modus Tollens)以及三段论(Law of Syllogism)。在假言推理中,给定的前提中一个是包含前件和后件的假言命题,一个是性质命题,假言推理根据假言命题前后件之间的逻辑关系进行推理。其中,肯定前件假言推理是指性质命题肯定了假言命题的前件,从而推理出肯定的假言后件。例如,通过假言命题“如果今天是星期二(前件)。那么小明会去上班(后件)”以及性质命题“今天是星期二”,能推理出“小明会去上班”。而否定后件假言推理是指性质命题否定了假言命题的后件,从而推理出否定的假言前件。例如,通过前文的假言命题和性质命题“小明不会去上班”,能推出“今天不是星期二”。在假言三段论中,给定两个假言命题,且第二个假言命题的前件和第一个假言命题的后件的申明内容相同,可以推理出一个新的假言命题,其前件与第一个假言命题的前件相同,其后件与第二个假言命题的后件相同。例如,给定两个假言命题“如果小明生病了,那么小明会缺席”以及“如果小明缺席了,他将错过课堂讨论”,可以推理出“如果小明生病了,他将错过课堂讨论”。从以上的例子可以看出,演绎推理是一种形式化的逻辑推理。
归纳推理[2] 是一种自下而上的推理,是指基于已有的部分观察得出一般结论的过程。例如,如果到目前为止我们见到的天鹅都是白色的,那么由归纳推理得出天鹅很大概率是白色的。典型的归纳推理有归纳泛化(Inductive Generalization)、统计推理(Statistical Syllogism)。归纳泛化是指基于对个体的观察而得出可能适用于整体的结论,即在整体的一些样本中得到的结论可以泛化到整体上。例如,有20个球,每个球不是黑色的就是白色的,要估计黑球和白球大概的个数。可以从20个球中抽样4个球,如果发现4个球中有3个白色和1个黑色,那么可以通过归纳泛化推理出这20个球中可能有15个球是白色的,5个球是黑色的。而统计推理是将整体的统计结论应用于个体。例如,经统计,90%就读于某高中的同学都上了大学,如果小明是这所高中的同学,那么可以由统计推理得出小明有90%的概率会上大学。归纳推理是一种非形式化的推理,是由具体到一般的推理过程。它和演绎推理有本质的不同,因为即便是在最理想的归纳推理中,如果作为推理前提的部分已有观察为真,也不能保证结论一定成立,即在任何情况下前提的真值都不能完全肯定结论的真值。但在演绎推理中,如果前提均为真,那么一定可以推理得到结论也为真。
溯因推理[3] 也是一种逻辑推理,是在给定一个或多个已有观察事实O(Observation),并根据已有的知识 T(Theory)推断出对已有观察最简单且最有可能的解释的过程。例如,当一个病人显示出某种病症,而造成这个病症的原因可能有很多时,寻找在这个病人例子里最可能的原因的过程就是溯因推理。在溯因推理中,要使基于知识T而生成的对观察O的解释E是合理的,需要满足两个条件,一是E可以由T和O经过推理得出,可以是演绎、归纳推理等多种方式;二是 E 和 T 是相关且相容的。例如,我们知道下雨了马路一定会湿(T),如果观察到马路是湿的(O),可以通过溯因推理得到很大概率是因为下雨了(E)。溯因推理是归纳推理的一种,因为整个推理过程的前提和结论并没有必然的关系。
类比推理[4] 可以看作只基于对一个事物的观察而进行的对另一个事物的归纳推理,是通过寻找两者之间可以类比的信息,将已知事物上的结论迁移到新的事物上的过程。例如,小明和小红是同龄人,他们都喜欢歌手A和歌手B,且小明还喜欢歌手C,那么通过类比推理可以得出小红也喜欢歌手 C。由于被类比的两个事物虽然有可类比的信息,却并不一定同源,而且有可能新推理出的信息和已知的可类比信息没有关系,所以类比推理常常会导致错误的结论,称为不当类比。例如在上例中,如果歌手 C 和歌手 A、歌手 B 完全不是一种类型或一个领域的歌手,那么小明喜欢歌手C与他喜欢歌手A和歌手B 是完全无关的,所以将“喜欢歌手 C”的结论应用到小红身上不合适。造成不当类比的原因有很多,包括类比事物不相干、类比理由不充分以及类比预设不当等。尽管类比推理的结论相较于前面介绍的三种推理得到的结论错误率更高,但类比推理依然是一种普遍存在的推理方式。
除了以上介绍的四种常见的逻辑推理,还有很多其他类型的推理。例如,根据不确定的观察信息以及不确定性的知识进行推理的不确定性推理,不确定性推理与前述四种推理方式的最大区别是其所能利用的推理信息都具有很大的不确定性。又例如在知识演变的过程中,根据原有的推论可否被推翻可以分为不会被推翻的单调推理以及可能会被推翻的非单调推理。从推理过程精确性来看,又可分为精确推理和模糊推理。
不同的研究领域也有各自的推理问题。例如,在自然语言处理领域,典型的问题是自然语言推理(Natutal Language Inference),其任务判断两个给定句子的蕴涵关系,给定的两个句子一个前提(Premise),一个是假设结论(Hypothsis),目标是判断在给定前提句子的情况下是否可以推理出假设结论的句子。答案分为三种,包括:表示假设结论句子和前提句子矛盾的“冲突(Contradiction)”、表示可以由前提句子推出假设结论句子的“蕴涵(Entailment)”以及表示前提句子和假设结论既不冲突也不蕴涵的“中立(Neutral)”。例如,前提句子“正在进行一场男子足球比赛”和假设结论句子“几个男运动员们在打比赛”应判断为“蕴涵”,而前提句子“两个小女孩在笑”和结论句子“两个小女孩因为这周末要去游乐场很开心”应判断为“中立”,将“一个男子沉睡在梦乡”和“男子眨了眨眼睛”判断为“冲突”。在计算机视觉领域也有视觉推理(Visual Reasoning),一般任务为根据给定的图片回答特定的需要推理的问题。例如,给定一个包含多个不同色彩、不同形状的几何体图片,回答问题“图中最小的正方体右边的几何体是什么颜色”。在知识图谱相关的研究中,也有面向知识图谱的推理,下面将重点介绍面向知识图谱的推理。
6.1.2 面向知识图谱的推理
面向知识图谱的推理主要围绕关系的推理展开,即基于图谱中已有的事实或关系推断出未知的事实或关系[5] ,一般着重考察实体、关系和图谱结构三个方面的特征信息。如图6-1所示为人物关系图推理,利用推理可以得到新的事实(X, isFatherOf, M),以及得到规则isFatherOf(x, y)<= fatherIs(y,x)等。具体来说,知识图谱推理主要能够辅助推理出新的事实、新的关系、新的公理以及新的规则等。
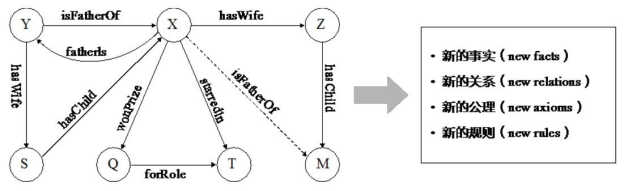
图6-1 人物关系图推理
一个丰富、完整的知识图谱的形成会经历很多阶段,从知识图谱的生命周期来看,不同的阶段都涉及不同的推理任务,包括知识图谱补全[6] 、不一致性检测、查询扩展等。将不同且相关的知识图谱融合为一个是一种有效地完善和扩大知识图谱的方式,而融合的过程包含两个重要的推理任务:有实体对齐(Entity Alignment)[7] 和关系对齐(Relation Alignment),关系对齐也叫作属性对齐(Property Alignment)。即识别出分别存在两个知识图谱中的两个实体实际上表示的是同一个实体,或者两个关系是同一种语义的关系,从而在知识图谱中将其对齐,形成一个统一的实体或关系。由于现实世界的知识千千万万,想要涵盖所有的知识是很难的,所以知识图谱的不完整性很明显,在对知识图谱进行补全的过程中,链接预测是一种典型的推理任务[8] 。知识图谱中的三元组可以通过人工定义得到,也可以通过文本抽取得到。由于人工知识的局限性以及算法的不确定性,一个知识图谱中不可避免地会存在冲突的信息,所以不一致性检测也是知识图谱中重要的推理任务,即检测知识图谱中有冲突或不正确的事实。存储了众多知识的知识图谱的一个重要作用是提供知识服务,为相关的查询返回正确的相关知识信息,但查询的模糊以及知识图谱本身的语义丰富性容易造成查询困难,而推理有利于查询重写,有效地提升查询结果的质量。
知识图谱的推理的主要技术手段主要可以分为两大类:基于演绎的知识图谱推理,如基于描述逻辑[9] 、Datalog、产生式规则等;基于归纳的知识图谱推理,如图6-1所示的路径推理[10] 、表示学习[11] 、规则学习[12] 、基于强化学习的推理[13] 等。以演绎推理为核心的知识图谱推理主要是基于描述逻辑、DataLog 等进行的,而以归纳推理为核心的知识图谱推理主要是围绕对知识图谱图结构的分析、对知识图谱中元素的表示学习、利用图上搜索和分析进行规则学习以及应用强化学习方法等进行的。下面分别从这两类展开,介绍不同的推理实现方法。

