2.2 人工智能早期的知识表示方法

知识是智能的基础。人类智能往往依赖有意或无意运用已知的知识。与此类似，人工智能系统需要获取并运用知识。这里有两个核心问题：怎么表示知识？怎样在计算机中高效地存储与处理知识？本章主要阐述第一个核心问题。

2.2.1 一阶谓词逻辑

一阶谓词逻辑（或简称一阶逻辑）（First Order Logic）是公理系统的标准形式逻辑。不同于命题逻辑（Propositional Logic），一阶逻辑支持量词（Quantifier）和谓词（Predicate）。例如，在命题逻辑里，以下两个句子是不相关的命题：“John MaCarthy 是图灵奖得主”（p）、“Tim Berners-Lee是图灵奖得主”（q）。

但是，在一阶逻辑里，可以用谓词和变量表示知识，例如，图灵奖得主（x）表示 x是图灵奖得主。这里，图灵奖得主是一元谓词（Predicate）,x 是变量（Variable），图灵奖得主（x）是一个原子公式（Atomic Formula）。Ø 图灵奖得主（x）是一个否定公式（Negated Formula）。在上面的例子中，若x为John MaCarthy，图灵奖得主（x）为第一个命题p。若x为Tim Berners-Lee，图灵奖得主（x）为第二个命题q。

1.一阶谓词逻辑优点

●结构性。能把事物的属性以及事物间的各种语义联想显式地表示出来。

●严密性。有形式化的语法和语义，以及相关的推理规则。

●可实现性。可以转换为计算机内部形式，以便用算法实现。

2.一阶谓词逻辑缺点

●有限的可用性。一阶逻辑的逻辑归结只是半可判定性的。

●无法表示不确定性知识。

2.2.2 霍恩子句和霍恩逻辑

霍恩子句（Horn Clause）得名于逻辑学家 Alfred Horn^[6] 。一个子句是文字的析取。霍恩子句是带有最多一个肯定（positive）文字的子句，肯定文字指的是没有否定符号的文字。例如，Øp₁ ∨…∨Øp_n ∨ q 是一个霍恩子句，它可以被等价地写为（p₁ ∧…∧p_n ）→ q。Alfred Horn于1951年撰文指出这种子句的重要性。

霍恩逻辑（Horn Logic）是一阶逻辑的子集。基于霍恩逻辑的知识库是一个霍恩规则的集合。一个霍恩规则由原子公式构成：B₁ ∧…∧ B_n → H，其中 H 是头原子公式， B₁ ,…,B_n 是体原子公式。事实是霍恩规则的特例，它们是没有体原子公式且没有变量的霍恩规则。例如，→图灵奖得主（Tim Berners-Lee）是一个事实，可以简写为图灵奖得主（Tim Berners-Lee）。

1.霍恩逻辑的优点

●结构性。能把事物的属性以及事物间的各种语义联想显式地表示出来。

●严密性。有形式化的语法和语义，以及相关的推理规则。

●易实现性。可判定，可以转换为计算机内部形式，以便用算法实现。

2.霍恩逻辑的缺点

●有限的表达能力。不能定义类表达式，不能够任意使用量化。

●无法表示不确定性知识。

2.2.3 语义网络

语义网络是由 Quillian 等人提出用于表达人类的语义知识并且支持推理^[3] 。语义网络又称联想网络，它在形式上是一个带标识的有向图。图中“节点”用以表示各种事物、概念、情况、状态等。每个节点可以带有若干属性。节点与节点间的“连接弧”（称为联想弧）用以表示各种语义联系、动作。语义网络的单元是三元组：（节点1，联想弧，节点2）。例如（Tim Berners-Lee，类型，图灵奖得主）和（Tim Berners-Lee，发明，互联网）是三元组。由于所有的节点均通过联想弧彼此相连，语义网络可以通过图上的操作进行知识推理。

1.语义网络的优点

1）联想性。它最初是作为人类联想记忆模型提出来的。

2）易用性。直观地把事物的属性及其语义联系表示出来，便于理解，自然语言与语义网络的转换比较容易实现，故语义网络表示法在自然语言理解系统中的应用最为广泛。

3）结构性。语义网络是一种结构化的知识表示方法，对数据子图特别有效。它能把事物的属性以及事物间的各种语义联想显式地表示出来。

2.语义网络的缺点

1）无形式化语法。语义网络表示知识的手段多种多样，虽然灵活性很高，但同时也由于表示形式的不一致提高了对其处理的复杂性。例如，“每个学生都读过一本书”可以表示为多种不同的语义网络，例如图2-2和图2-3中的语义网络。在图2-2中，GS表示一个概念节点，指的是具有全称量化的一般事件，g 是一个实例节点，代表 GS 中的一个具体例子，而 s 是一个全称变量，是学生这个概念的一个个体，r 和 b 都是存在变量，其中r 是读这个概念的一个个体，b 是书这个概念的一个个体，F 指 g 覆盖的子空间及其具体形式，而∀代表全称量词。而图2-3则把“每个学生都读过一本书”表示成：任何一个学生s₁ 都是属于读过一本书这个概念的元素。

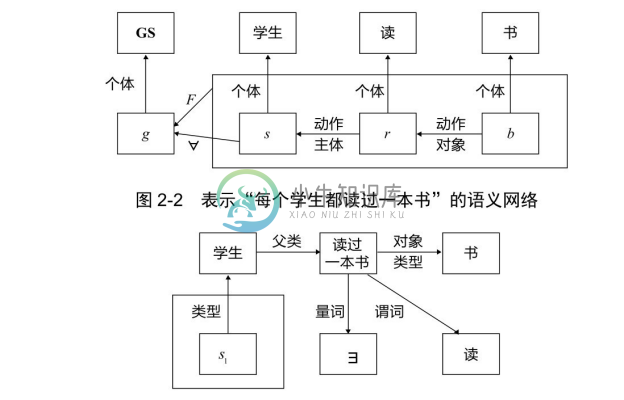
图2-3 表示“每个学生都读过一本书”的语义网络

2）无形式化语义。与一阶谓词逻辑相比，语义网络没有公认的形式表示体系。一个给定的语义网络表达的含义完全依赖处理程序如何对它进行解释。通过推理网络而实现的推理不能保证其正确性。此外，目前采用量词（包括全称量词和存在量词）的语义网络表示法在逻辑上是不充分的，不能保证不存在二义性。

2.2.4 框架

框架（Frame）最早由Marvin Minsky在1975年提出^[7] ，目标是更好地理解视觉推理和自然语言处理。其理论的基本思想是：认为人们对现实世界中各种事物的认识都以一种类似于框架的结构存储在记忆中。当面临一个新事物时，就从记忆中找出一个合适的框架，并根据实际情况对其细节加以修改、补充，从而形成对当前事物的认识。

框架是一种描述对象（事物、事件或概念等）属性的数据结构。在框架理论中，类是知识表示的基本单位。每个类有一些槽，每个槽又可分为若干“侧面”。一个槽用于表示描述对象的一个属性，而一个侧面用语表示槽属性的一个方面，槽和侧面都可以有属性值，分别称为槽值和侧面值。除此之外，框架还允许给属性设默认值，以及设立触发器以维护框架。

1）下面是框架的基本组成的一个示例：

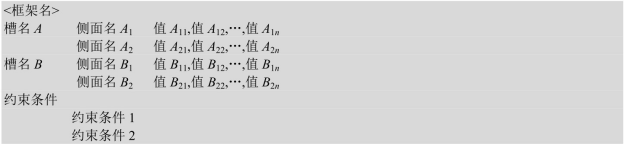
2）表2-1给出一个带变量框架实例。

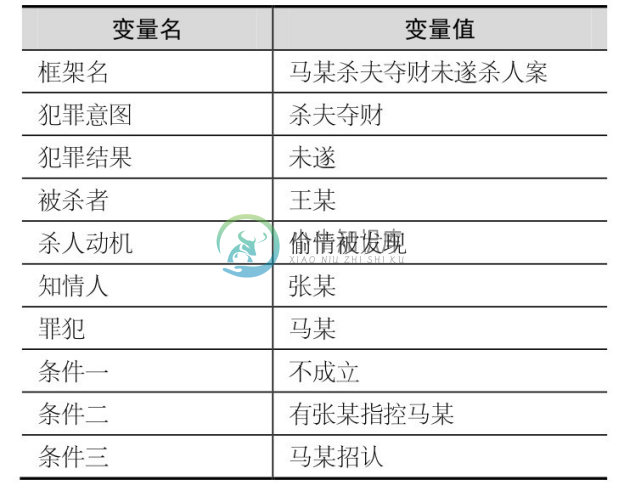
如果把框架“tx 未遂杀人案”的变量赋值，可以得到下面的一个框架实例，如表2-2所示。

表2-1 带变量框架实例

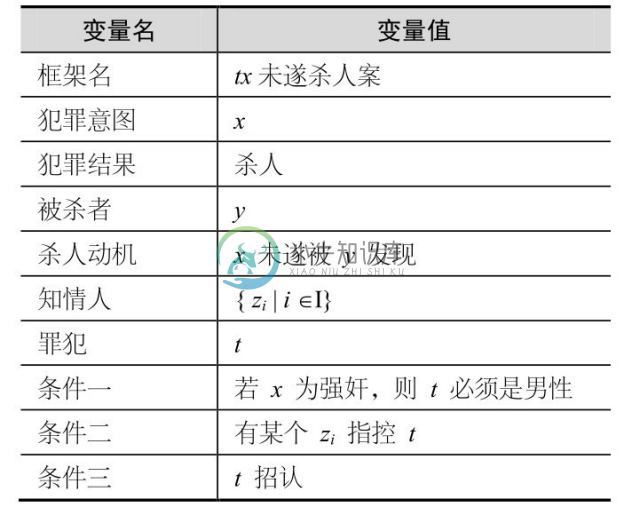
表2-2 变量赋值框架实例

1.框架的优点

1）结构性：能把事物的属性以及事物间的各种语义联想显式地表示出来。

2）框架对于知识的描述比较全面，支持默认值以及触发器。

2.框架的缺点

1）框架的构建成本非常高，对知识库的质量要求非常高。

2）默认值会增大推理的复杂度。

3）无法表示不确定性知识。

2.2.5 描述逻辑

描述逻辑是一阶逻辑的一个可判定子集。最初由Ronald J.Brachman在1985年提出。描述逻辑可以被看成是利用一阶逻辑对语义网络和框架进行形式化后的产物。描述逻辑一般支持一元谓词和二元谓词。一元谓词称为类，二元谓词称为关系。描述逻辑的重要特征是同时具有很强的表达能力和可判定性。描述逻辑近年来受到广泛关注，被选为 W3C 互联网本体语言（OWL）的理论基础。

1.描述逻辑的优点

1）结构性。能把事物的属性以及事物间的各种语义联想显式地表示出来。

2）严密性。有形式化的语法和语义，以及相关的推理规则。

3）多样性。具有大量可判定的扩展，以满足不同应用场景的需求。

4）易实现性。可判定，可以转换为计算机内部形式，以便用算法实现。

2.描述逻辑的缺点

1）有限的表达能力。不支持显式使用变量，不能够任意使用量化。

2）无法表示不确定性知识。