5.4 实例层的融合与匹配
在实际应用中，由于知识图谱中的实例规模通常较大，因此针对实例层的匹配成为近年来知识融合面临的主要任务。实例匹配的过程虽然与本体匹配有相似之处，但实例匹配通常是一个大规模数据处理问题，需要在匹配过程中解决其中的时间复杂度和空间复杂度问题，其难度和挑战更大。
5.4.1 知识图谱中的实例匹配问题分析
在过去的几十年中，本体在知识表示中起着举足轻重的作用。人们通过艰苦的努力，建立了很多描述通用知识的大规模本体，并将其应用于机器翻译、信息检索和知识推理等应用。与此同时，很多领域中的研究人员为了整合、归纳和分享领域内的专业知识，也建立了很多领域本体。这些本体的规模正随着人类知识的增长而变得越来越大。近年来，不同领域知识的交叉和基于不同大本体的系统间的交互都提出了建立大规模本体间映射的需求。然而，多数映射系统不仅无法在用户可接受的时间内给出满意的映射结果，而且还往往会由于匹配过程申请过大的内存空间而导致系统崩溃。因此，大规模本体映射问题对映射系统的时间复杂度、空间复杂度和映射结果质量都提出了严峻的考验，成为目前本体映射研究中的一个挑战性难题。本章将在分析现有几种大规模本体映射方法的基础上，提出一种新的大规模本体映射方法，该方法具有较好的时间复杂度和空间复杂度，并能保证映射结果的质量。
从20世纪80年代起，人们就一直努力创建和维护很多大规模的本体，这些本体中的概念和关系规模从几千个到几十万个不等，有些本体的实例数目甚至达到亿级。这些大本体总体上可划分为三类：通用本体，即用于描述人类通用知识、语言知识和常识知识的本体，如Cyc、WordNet和SUMO等；领域本体，各个领域中的研究人员也建立了很多专业领域中的本体，如生物医学领域中的基因本体和统一医学语言系统本体 UMLS；企业应用本体，为了有效管理、维护和利用拥有的大量数据，很多企业都利用本体对自身的海量数据进行重组，以便为用户提供更高效和智能的服务。出于商业保密的目的，这些企业本体通常并不公开。大规模本体在机器翻译、信息检索和集成、决策支持、知识发现等领域中都有着重要的应用。表5-4是对12个大规模知识图谱的调查结果，其中列举了各知识图谱中概念、关系、实例和公理的数目，表中横线表示没有获得对应数据；另外，由于一些本体创建时间较早，它们并没有按近年提出的本体模型来组织知识，因此只提供了所包含的术语数目。从调查结果可见，大规模知识图谱中的元素数庞大，尤其是实例数据较多。
表5-4 大规模知识图谱的规模调查
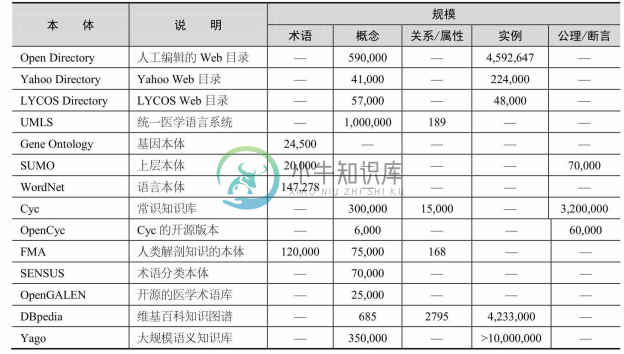
大规模知识图谱的创建和维护仍然具有分布性和自治性的特点，知识图谱间同样存在无法避免的异构问题。基于不同大规模知识图谱的系统间可能需要进行交互。一些应用需要借助映射对多个知识图谱进行集成，如Web搜索中需要集成Yahoo Directory和Google Directory。随着不同科学研究领域的交叉和融合，不同领域知识图谱中的知识有可能产生交叉重叠，如关于解剖学的本体需要用到 UMLS 本体中的语义信息。总之，大规模知识图谱间的异构现象依然普遍存在。在实际应用中，为集成同一领域中不同的大规模知识图谱，或者为满足基于不同大规模知识图谱的系统间的信息交互需求，都有必要建立大规模知识图谱间的匹配。
大规模知识图谱匹配是极具挑战性的任务。Reed和Lenat为将SENSUS、WordNet和UMLS等本体映射到Cyc中，通过训练本体专家和借助交互式对话工具等半自动手段，前后耗费了15年的时间才完成这项大规模本体映射项目[101] 。显然，人工和半自动的方法很难处理大规模知识图谱匹配问题，因此需要寻找有效的自动化方法。传统的模式匹配工作虽然提出处理大规模模式匹配的分治法[102,103] ，但数据库模式和 XML 模式都是树状结构，位于不同树枝的信息相对独立，适于采用分治思想处理。然而，知识图谱具有复杂的图结构，传统模式匹配的分治方法并不能直接应用于知识图谱匹配。
可处理大规模知识图谱匹配的系统方法并不多。例如，在2006年的 OAEI 评估中， 10个系统中只有4个完成了 anatomy 和 food 两个大规模本体匹配任务。在2007年的OAEI 中，参与评估的18个映射系统，只有2个完成了 anatomy、food、environment 和library这4个大规模知识图谱匹配任务。2008年参与OAEI评估的13个映射系统，只有2个完成了anatomy、fao、mldirectory和library这4个大规模知识图谱匹配任务，而完成通用知识图谱匹配任务vlcr的系统只有1个。由此可见，大多数公开的系统仍然不能处理大规模知识图谱匹配问题。
大规模知识图谱匹配问题对空间复杂度、时间复杂度和匹配结果质量都提出了严峻考验，下面给出具体分析。
1.空间复杂度挑战
在知识图谱匹配过程中，读入大规模知识图谱将占用相当一部分存储空间，随后的预处理、匹配计算和映射后处理均可能需要申请大量空间才能完成，这些步骤往往导致匹配系统无法得到足够的内存空间而崩溃。通常，知识图谱匹配中的主要数据结构（如相似矩阵）的空间复杂度是 O(n2 )，在处理大规模知识图谱匹配时，这样的空间复杂度会占用大量的存储资源。当系统申请的存储空间不能一次读入内存时，将造成操作系统不断在内存储器和虚拟存储器之间中进行数据交换；当操作系统无法满足映射系统的空间申请要求时，将导致内存不足的严重错误。很多匹配系统都采用二维数组来记录元素间的相似度矩阵，即使对于一个实例规模为5000的小型知识图谱，相似矩阵中的数值为双精度类型，则存储该矩阵所需的空间大约为200MB。因此，大规模知识图谱匹配中需要设计合理的数据结构，并利用有效的存储压缩策略，才能减小空间复杂度带来的负面影响。目前来说，只要选择合理的数据结构，并利用一些数据压缩存储技术，现有计算机存储能力基本能满足多数大规模知识图谱匹配的需求。因此，虽然空间复杂度是大规模知识图谱匹配中的一个难题，但并不是不可能克服的问题。
2.时间复杂度挑战
负责知识图谱读取和解析等操作的预处理过程和映射结果后处理过程一般不会成为匹配系统的时间瓶颈，知识图谱匹配系统的执行时间主要取决于匹配计算过程。为了得到最佳的映射结果，匹配过程需要计算异构实例间的相似度，早期大多数的知识图谱匹配系统的时间复杂度都是 O(n2 )（n 为元素数目）。虽然也有研究者提出O(n log(n))复杂度的匹配方法，但这种方法是以损失匹配质量为代价来换取匹配效率的。此外，不同匹配系统采用的匹配器在效率上差别很大，即求两个元素间的相似度这一过程所需要的时间复杂度存在差异，例如有的系统仅仅简单地计算元素标签的字符串相似度，有的则需要对知识图谱中的图做复杂的分析，二者之间的时间复杂度差别非常大；例如，我们通过实验比较发现，在本体映射系统 Lily 中，利用简单的编辑距离方法计算元素相似度的速度比利用语义描述文档的方法大约快1000倍。令计算两元素相似度过程的时间复杂度为t，则匹配系统的总时间复杂度可表示为 O(n2 t)。因此，降低大规模知识图谱匹配问题的时间复杂度除了要考虑减少匹配元素对的相似度计算次数（即 n2 ），还需要降低每次相似度计算的时间复杂度（即t）。
3.匹配结果质量挑战
在降低匹配方法的时间复杂度和空间复杂度的同时，有可能造成匹配结果质量降低。很多优秀的匹配方法往往比较复杂，如果在处理大规模知识图谱匹配时用简化的快速算法来代替，或者为了提高效率设置一些不能发挥算法优势的参数，都可能得不到满意的映射结果。此外，很多有效的匹配算法需要对知识图谱进行全局分析和整理，例如采用相似度传播的结构匹配方法等。然而，这种处理对大规模知识图谱来说并不可行，尽管可以采用简化或近似处理来替代，但由此得到的映射结果可能有损失。最后，一些算法采用分治的策略，将大规模知识图谱匹配问题转换为多个小规模匹配问题，但分治的过程会将原本相邻元素分割开，破坏某些实例语义信息的完整性，因此这部分位于边界位置的实例的匹配质量无法得到保证。
由于大量实际应用的需要，大规模知识图谱匹配问题备受关注。尽管目前能处理该问题的映射系统还较少，但一些研究者已进行了积极尝试，其中包括集成通用本体用于机器翻译[104] ，建立 Web Directory 之间的映射用于信息检索[105] ，以及匹配生物医学领域的本体用于不同医学系统间信息交互[106-108] 等。最近几年的 OAEI 评估也给出一些实际的大规模知识图谱匹配任务，虽然完成这类匹配任务的系统较少，但处理该问题的方法每年都得到改进。本文将现有的大规模知识图谱匹配方法划分为三类：基于快速相似度计算的方法、基于规则的方法和基于分治的方法。就目前来看，现有的大规模知识图谱匹配系统都能克服空间复杂度问题，因为匹配过程中需要的大量空间可以借助数据压缩技术（如将稀疏矩阵压缩存储）、外部数据库或临时文件等方式解决。因此，下面着重分析三类方法的时间复杂度。
5.4.2 基于快速相似度计算的实例匹配方法
这类方法的思想是尽量降低每次相似度计算的时间复杂度，即降低 O(n2 t)中的因素t，因此映射过程只能使用简单且速度较快的匹配器，考虑的映射线索也必须尽量简单，从而保证t接近常数O(1)。
基于快速相似度计算的方法使用的匹配器主要包括文本匹配器、结构匹配器和基于实例的匹配器等。很多基于文本相似的匹配算法时间复杂度都较低，但为达到快速计算元素相似度的目的，文本匹配器还应避免构造复杂的映射线索，例如映射线索只考虑元素标签和注释信息。大规模知识图谱匹配中的结构匹配器借助概念层次或元素邻居文本相似的启发式规则计算相似度，例如两个实例的父概念相似，则这两个实例也相似等；为避免匹配时间复杂度过高，这些启发式规则不能考虑太复杂的结构信息。
采用上述思想的系统虽然能勉强处理一些大规模知识图谱匹配问题，但其弊端也很明显。首先，匹配器只能利用知识图谱中少量的信息构造匹配线索，得到的匹配线索不能充分反映元素语义，这会导致降低映射结果质量。其次，系统效率受相似度计算方法影响较大，即t的少量变化会给系统的效率带来较大影响。
Mork和Bernstein尝试对FMA和GALEN两个大规模本体进行匹配[107] ，匹配过程采用了一些通用的文本匹配器和结构匹配器，他们指出这种匹配处理的时间复杂度和空间复杂度都很高。Ichise 等人实现了 Web Directory 的匹配[109] ，匹配方法依靠统计共享实例。此外，在相似度计算中，寻找最佳的相似函数和阈值也是一个重要问题，可采用最大可能消除匹配冗余计算的思想进行优化[110] 。在 OAEI2007的大规模本体匹配任务中，一些采用快速相似度计算思想的映射系统在计算时间上并没有优势，但其得到的映射结果质量却并不理想，例如，在 Anatomy 匹配任务中，采用简单文本匹配的 Prior+、Lily1.2和DSSim等系统在运行时间和结果质量上都并不突出。
5.4.3 基于规则的实例匹配方法
在大规模知识图谱中，为了从海量的实例数据中有效发现匹配实例对，寻找匹配规则是一条可行的思路。但由于数据源的异构性，处理不同的数据源需要的匹配规则不尽相同，规则匹配方法往往需要人类手工构建的规则来保证结果质量。为避免过多的人工参与。基于规则的方法易于扩展到处理大规模知识图谱中的实例匹配，甚至可以扩展到基于概率的方法[111] 。
上海交通大学的研究人员开发了一套基于EM算法的半监督学习框架以自动寻找实例匹配规则[112] ，其实例匹配过程如图5-12所示。该框架以迭代的方式来自动发现匹配规则，并逐步提高匹配规则集的质量，再利用更新后的规则集来寻找高质量的匹配对。具体地，数据集中少量具有owl:sameAs属性的现存匹配对被视为种子（Seeds），匹配规则被视为似然函数中需要被估计的参数。该方法利用一种基于图的指标来度量匹配的精确度，并作为EM算法的目标似然函数。在不同的匹配规则下，同一个匹配对的匹配置信度是不一样的，如何集成不同规则的置信度是一个很重要的问题。该方法引入 Dempster's rule [1] 来集成同一个匹配对的不同置信度。
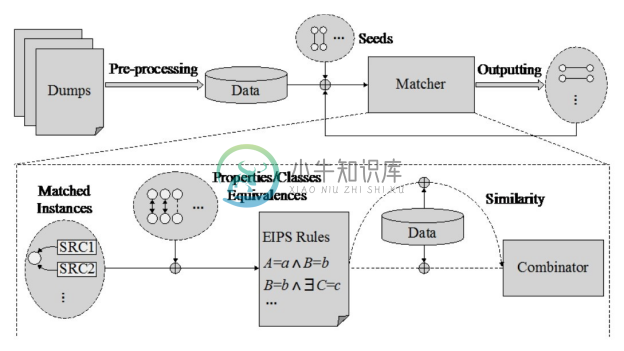
图5-12 基于规则挖掘的实例匹配过程[112]
在进一步介绍该方法之前，需要定义一些基础概念。
定义5.12 （实例等价）记作～I，代表了两个实例在现实世界中为同一个物体。URI不同的两个实例e1 ,e2 是等价的，当且仅当＜e1 , e2 ＞ ∈～I。
定义5.13 （匹配）由匹配器发现的一个匹配表示为＜e1 , e2 , conf＞，其中e1 , e2 为实例，conf为匹配的置信度，它们满足P（＜e1 , e2 ＞∈～I）=conf。
如图5-12所示，预处理完成后，实例就包含了相应的属性-值对（Property-Value Pairs）信息。然后，种子匹配对被导入系统中，用来驱动发现新的匹配，高质量的新匹配对会加入种子匹配对中以进行下一轮迭代。重复迭代步骤直至满足终止条件。
前面提到，该框架通过学习规则来推导实例之间的等价关系。首先，已知匹配对中的属性等价关系（Property Equivalence）会被挖掘；然后，这些规则被利用到未匹配实例上发现新的等价实例。一些属性等价的例子如下所示：
rdfs:label≈gs:hasCommonName
foaf:name≈gs:hsCanonicalName
dbpedia:phylum≈gs:inPhylum
在 dbpedia.org 中定义的属性 dbpedia:phylum 和 geospecies.org 中定义的属性gs:inPhylum有相同的内在含义：它们对应的值在生物分类中都属于同一个等级。
实例等价和属性等价可推导出如下规则：如果两个实例e1 , e2 满足
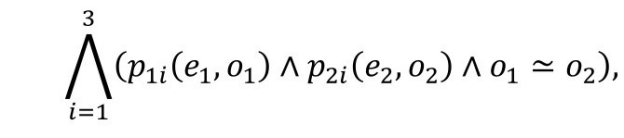
则有＜e1 , e2 ＞∈～I。（p（e, o）是三元组＜e, p, o＞的函数式表示，o1 ≃o2 表示o1 和o2 指向同一实例或者字面值相等）。
这样的规则可以推导出大量的等价实例，从而完成实例匹配。
定义5.14 （属性-值对等价）给定两个隐含等价属性（p1 , p2 ）和两个值（o1 , o2 ），属性-值对＜p1 , o1 ＞和＜p2 , o2 ＞等价当且仅当 ＜o1 , o2 ＞∈～I（o1 ,o2 为实例），或者o1 =o2 （o1 ,o2 为字面值），记作～P。
将这种等价关系拓展到属性-值对集，给定一个实例 e 和属性集合 P，属性-值对集定义为PVe,P ={＜p,o＞|p∈P,＜e,p,o＞∈G}。
定义5.15 （等价属性-值对集）给定两个实例（e1 , e2 ）和一个等价属性对集（＜P1 , P2 ＞），两个键值对集
等价当且仅当存在一个从
到
的双射f∈～P，记作～S。
定义5.16 （逆功能属性集）一个等价属性对集 eps 是一个逆功能属性集（Inverse Functional Property Suite），当且仅当其满足若
，则＜e1 ,e2 ＞∈～I。
定义5.17 （逆功能属性集规则）逆功能属性集规则（IFPS Rule）基于逆功能属性集eps。对于所有eps里的属性对＜pi1 , pi2 ＞，一个IFPS 规则有如下形式：
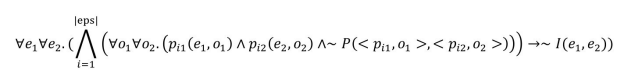
定义5.18 （扩展的逆功能属性集规则）与 IFPS 规则相似，扩展的逆功能属性集规则（Extended IFPS Rule）基于逆功能属性集 eps。对于所有 eps 里的属性对＜pi1 ,pi2 ＞, EIFPS 规则有如下形式：
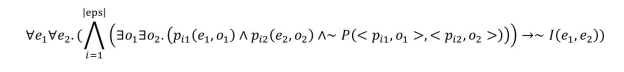
根据以上定义，该方法实现了一个基于EM算法的实例匹配框架，输入为待匹配三元组、初始匹配对阈值，输出为匹配结果集与 IFPS 规则集。该框架利用 EM 算法迭代：E步，根据已经获得的 EIFPS 规则计算实例对应的置信度，把置信度高于阈值的对应放到匹配结果中；M步，根据现有的匹配结果挖掘EIFPS规则，等同于最大化似然函数。
这里引入匹配图来估计算法的匹配进度，匹配图是一个无向带权图，图中的每一个顶点代表一个实例，边代表两个实例匹配的置信度。根据EIPFS规则集合，可以从所有的三元组中提取出一个匹配图。EM 算法中的似然函数定义为提取出的匹配图和实际匹配图的相似程度：给定一个匹配图M,EM算法中的似然函数被定义为：L（θ;M）=Pr（M|θ）。采用准确度优先策略，可以得到以下的近似公式，用精确度来代表在一个 EIPFS 规则集合下，提取出来的对应图和真正的对应图之间的关系：
L（θ;M）≈Precision（M|θ）
最后，求出的匹配图M的精确度等于M中被连接的成分除以M中边的数量：
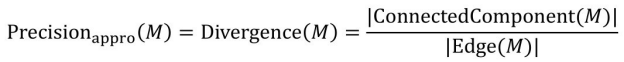
同一个匹配对可能会由不同的EIFPS规则导出，该匹配对有多个匹配置信度，因此集成两个置信度是一个很有必要的工作。传统上会选择取两者之间的较大值，但这种集成方式只利用了一次匹配的信息，我们倾向于认为利用了两次匹配的信息得出的结果更为准确。这里给出了另外的两种集成方式，具体如下：
第1种是基于概率理论：
conf1 ⊕conf2 =1−（1−conf1 ）（1−conf2 ）
第2种利用了一种特殊性形式下的贝叶斯理论的泛化理论（Dempster-Shafer theory）：
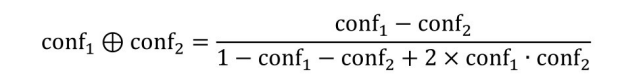
该方法先后用在 DBpedia、GeoNames、LinkedMDB、GeoSpecies 等知识图谱间进行实例匹配。该方法解决了zhishi.me等知识图谱构建中的实例匹配问题[113] 。
5.4.4 基于分治的实例匹配方法
分治处理方法的思想是降低相似度计算总的时间复杂度，即降低 O(n2 t)中的因素 n2 。采用分治策略，将大规模知识图谱匹配划分为k 个小规模的知识图谱匹配后，匹配的时间复杂度降为O(kn'2 t')，其中t’表示计算两元素间相似度的时间复杂度，与分治前可能不同，n’为分治处理后的小本体的平均规模，即
，所以分治处理的时间复杂度又可表示为
。由此可见，系统效率取决于能将原有问题划分为多少个小规模。最常用的分治策略是将大规模本体划分为若干个小知识图谱，然后计算这些小知识图谱间的匹配。
分治法的思想已被用于处理大规模数据库模式和XML模式匹配问题[102,114] 。Rahm和Do提出一种基于模式片段（fragment）的大规模模式匹配分治解决方法，该方法包括4个步骤：①分解大模式为多个片段，每个片段为模式树中的一个带根节点的子树，若片段过大，则进一步进行分解，直到规模满足要求为止；②识别相似片段；③对相似片段进行匹配计算；④合并片段匹配结果即得到模式匹配结果。这种方法能有效处理大规模的模式匹配问题，然而由于知识图谱是图结构，模式的片段分解方法并不适用于划分大规模知识图谱。
本体模块化方法是对大规模本体进行划分的一种直观手段。已有多种本体模块化方法被提出。Grau等人通过引入语义封装的概念，利用ε-connection[115] 将大本体自动划分为多个模块，该模块化算法可保证每个模块都能够捕获其中全部元素含义的最小公理集。然而，这种方法在实际应用中效果并不好。例如，该算法只能将GALEN划分为2个模块，只能将NCI本体划分为17个模块，而且所得模块的规模很不均匀，即某些模块对本体映射来说还是太大了，因此该方法并不能解决将大本体划分为适当大小的问题。Grau 等人还提出了其他确保局部正确性和完整性模块化算法[116] ，但结果显示该算法也不能解决模块规模过大的问题。例如，该算法对 NCI 本体划分会得到概念数目为15254的大模块，而对 GALEN 本体模块化则失败。此外，一些本体模块化工作的目标是获得描述特定元素集含义的模块[117,118] ，而不能将本体划分为多个不相交或只有少量重叠的模块。Stuckenschmidt 和 Klein 通过利用概念层次结构和属性约束，给出一种本体模块化方法[119] ，但结果显示该方法得到的模块规模通常太小，并且只能处理概念结构层次构成的本体。总的来说，上述模块化工作并非以服务大规模本体映射为目的，它们都强调模块语义的完备性和正确性，而忽略给模块分配适当的规模。特别是知识图谱中存在大量的实例，上述模块化方法难以对大量的实例进行有效的划分。
目前采用分治思想处理大规模本体映射的典型系统有Malasco、Falcon-AO、Lily等。Malasco [2] 是 Paulheim 提出的一种基于分治思想的大规模 OWL 本体映射系统[120] ，该系统实际上是一个大规模本体映射框架，可重用现有的匹配器和本体模块化方法。Malasco 提供了三种本体划分算法：①基于RDF声明[121] 的朴素划分算法；②Stuckenschmidt和Klein的模块化算法[119] ;③基于Grau的ε-connection模块化算法[116] 。Paulheim在大规模本体上对模块化处理前后的匹配结果进行了比较和优化处理：在不做优化处理时，映射结果的精度与不做模块化处理前相比有50%的损失；采用覆盖模块化方法进行优化后，精度损失降低到20%，覆盖模块化是为了弥补模块交界部分的信息损失；为匹配结果选取合适的相似度阈值后，精度损失降低到5%。Paulheim 的工作表明了模块化方法经过适当优化，是可以处理大规模本体映射问题的。
Falcon-AO 中采用一种基于结构的本体划分方法解决大规模本体映射问题[122] 。该方法首先通过分析概念层次、属性层次以及属性约束信息，然后利用聚类方法将本体中的元素划分为不相交的若干个集合，再利用 RDF 声明恢复每个集合中的语义信息，从而完成本体划分。接着，基于预先计算的参照点，对不同的本体块进行匹配，匹配计算只在具有较高相似度的块间进行。该方法的划分算法可将本体元素划分为合适大小的集合，从而能利用现有的匹配器发现映射。Falcon-AO 的结果也表明该算法并未使映射结果质量有明显损失。
基于本体划分的分治处理方法较为直观，但该方法存在的主要缺点在于划分后的模块边界存在信息损失，即处于模块边界的元素的语义信息有可能不完整，由此得到的映射结果必然会有损失。一般来说，划分得到的块越多，边界语义信息损失也越多，因此，模块大小和边界信息损失是不可调和的，在实际应用中需要合理权衡。Malasco 中的覆盖模块优化方法是一种对该缺点的补救处理。
Lily 则巧妙地利用了大规模知识图谱匹配中的匹配局部性特点，不直接对知识图谱进行分块，而通过一些确定的匹配点（称为锚点）自动发现更多的潜在匹配点，从而达到实现高效实例匹配的目的且无须进行知识图谱划分。该方法的优点是实现过程简单，同时避免了划分知识图谱造成的语义信息损失。
1.基于属性规则的分块方法
由于在知识图谱中实例一般都有属性信息，所以根据属性来对实例进行划分，减少实例匹配中的匹配次数以提高匹配的效率，成为一种很自然的思想。类似的方法在关系数据库领域和自然语言处理领域中的实体消解中早已得到了广泛的应用。如图5-13所示，对于数据库中的一组实例 r、s、t、u、v，为了在匹配的过程中减少匹配计算的次数，可以利用实例的属性值对其进行划分。这里如果用“zip”进行划分，则得到一种划分结果：SC1 ={{r} {s,t},{u,v}}，其中包含了3个块；如果用“姓的首字母”划分，则又得到了一种划分结果：SC2 ={{r,s} {t},{u,v}}。可见，不同的划分依据得到的结果也不相同。这种方法面临几方面的挑战：①划分规则，划分规则的确定需要对数据有深刻了解并由人工进行分析得到，特别是划分结果能否完全覆盖所有实例，即分块的完备性；②分块的冗余，在实际的大规模数据中也很难保证得到的集合中的各个块没有交叉，也就是一些实例被同时分到了多个块中，这种冗余会降低匹配效率，也会引起匹配结果的冲突，通常可以用冗余率判断分块的冗余程度；③分块的选择，不同的划分得到不同的集合，如何评价一种划分得到的集合是否最佳是很困难的，因此在匹配中往往会同时采用多种划分得到的结果，选择那些分块结果进行匹配是一个难题；④匹配结果的整合，在采用多种划分结果进行匹配的基础上，再把匹配结果整合起来是一个难题，其中要解决一些匹配结果的冲突或不一致问题。
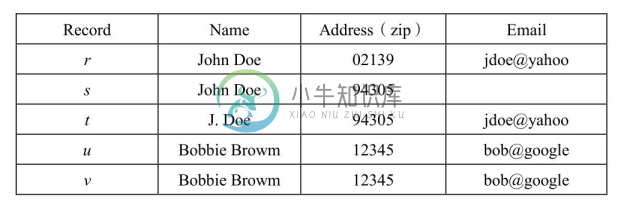
图5-13 数据库中的一组实例数据
为了降低分块结果的冗余性，一种典型的方法是实现将属性进行聚类，在聚类的基础上再进行分块[123] 。但是无论使用什么属性分块技术，都面临着两个矛盾的问题：①匹配效果，分块越细，造成的分块冗余越多，但未命中的匹配也越少，即匹配效果会更好；②匹配性能，分块越细，造成的不必要匹配计算越多，降级了匹配的性能。所以，很多基于属性分块的方法都力图在匹配效果和匹配性能上达到平衡。可以通过对分块效果进行预估来判断什么分块规则在效果和性能上较为平衡[124] 。为了降低分块冗余，可以把这种冗余的判断视为一个二分类问题，通过监督学习方法实现分块结果的精细调整[125] 。
2.基于索引的分块方法
受数据库领域中索引分块思想的启发，实例匹配也可以借助实例相关信息进行分块。VMI 是清华大学研究人员提出的一套在大规模实例集上解决实例匹配任务的算法框架[126] ，该方法的主要思想是运用了多重索引与候选集合，其中将向量空间模型和倒排索引技术相结合，实现对实例数据的划分。在保证了高质量匹配的前提下，VMI 模型显著地减少了实体相似度计算的次数，提高了整体匹配效率。
为了利用实例中包含的信息，VIM方法将实例信息总结分为以下六类：
（1）URI。 URI 实例的唯一标识符，如果两个实例有相同的 URI，那么可以判定这两个实例相同。
（2）元信息。 实例的元信息包含实例的模式层信息，如实例所属的类、实例的属性等。
（3）实例名。 人们利用实例名（标签）指代现实世界中的实例。一个实例的名称可从RDFS:label属性获取。在匹配两个实体时，一个直观且有效的方法是比较名字。因此，实例名在实例匹配任务中是一种非常重要的信息。
（4）描述性属性信息。 这类属性值由实例的描述性语言构成，典型的例子是RDFS:comment属性。
（5）可区分属性信息。 这类属性不是实例的描述，而是可以用来区分实例的属性。例如，性别属性为男的实例不与为女的实例匹配，拥有相同电子邮件地址的两个实例有极高的可能匹配。
（6）邻居信息。 实例根据不同的属性信息可以连接到相邻的实例。例如实例 Person1有一个属性haswife，对应的值是 Person2，那么 Person1就和 Person2连接起来了，同时称Person1和Person2互为邻居。
传统方法的思想是利用实例的相关信息对来自不同信息源的实例进行匹配。在源本体Os 中给定一个实例i，计算i与目标本体Ot 中的每一个实例的相似度，然后选取匹配对。显然对于大规模知识图谱而言，这种暴力搜索方式的计算花销太大。VMI 选择先利用倒排索引的方式划分待选匹配集，然后在各个匹配集中进行匹配操作，从而大大缩小了搜索空间，实现了匹配性能的优化。
该方法的处理过程如图5-14所示，其主要流程包括4个步骤。
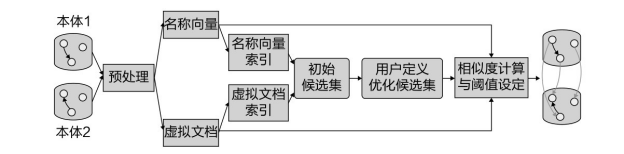
图5-14 VMI实例匹配过程[126]
（1）向量构造与索引。 VMI 对实例包含的不同类型的信息进行了向量化处理，然后对这些向量构建待排索引，即向量中的每一项都索引到前一步构造的向量中包含该项的实例。
（2）候选匹配集。 利用倒排索引检索出候选的匹配对，再利用设计好的向量规则形成候选匹配集。
（3）优化候选匹配集。 根据用户自定义的属性对和值模式对候选匹配集合进行优化，去除不合理的候选匹配。
（4）计算匹配结果。 利用实例的向量余弦相似度计算实例对的相似度，通过预设的阈值提取出最终的实例匹配结果。
VMI 方法首先为每个实例构建了名称向量和虚拟文档。为了获取名称向量，VMI 首先检查一个实例是否有rdfs:label这个属性，或者有没有其他与名字属性相关的值，如果没有，则选择 URI 中的一部分作为名称向量。构建名称向量的过程为：将抽取出来的名称进行分词；对分词结果进行停用词过滤；根据分词结果，统计出词频并构建向量。
实例的虚拟文档包含了除名字外的其他信息，如邻居节点的名称向量和邻居节点的信息。实例i的邻居节点对应的向量为：
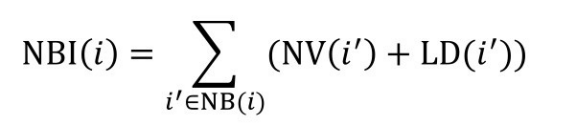
式中，NBI（i）表示邻居节点的信息所构成的向量；NB（i）表示所有邻居节点构成的集合；NV（i′ ）表示邻居节点的名称向量；LD（i′ ）表示邻居节点的本地描述信息。
最终构建出来的虚拟文档向量如下所示：
VD（i）=LD（i）+γ∙NBI（i）
虚拟文档由实例本身的本地描述信息向量和节点的信息向量构成，并取两者的线性组合，其中参数γ表示邻居文档信息的重要性。
VMI 方法认为名称向量中的每一个词都是重要的，所以对所有的分词项进行构建倒排索引的操作，如对于一个分词项i,VMI维护一个所有向量中包含i的列表。
接下来，VMI按照如下的规则选择候选实例匹配集合：
规则1,2个名称向量维数都大于5，且两者名称向量中至少有2个关键词相同。
规则2,2个名称向量维数都小于5，且两者名称向量中至少有1个关键词相同。
规则3,2个虚拟文档向量中至少有1个相同的关键词。
以上的规则可以在倒排索引的基础上快速实现，从而实现对实例的划分。
上面规则只能简单地排除不可能匹配上的匹配对，因此还要对待选匹配集进行优化。VMI 根据用户设定的属性进行筛选，有两种可能的情况：①检查用户设定的属性在待匹配的实例中是否存在；②检查用户设定的属性对应的值是否一致。VMI 将对应属性不一致的匹配对排除，实现候选实例匹配对的进一步过滤。
当待匹配集构建完成以后，就可以利用向量空间模型计算两个实例在向量空间中的距离，如余弦相似度。Vs ,Vt 代表待匹配的实例向量，vsi ,vti 代表向量对应的分量。VMI 只计算待匹配实例与待匹配集里的向量对应的距离，这样大大降低了计算的复杂度。最后，将名称向量相似度和虚拟文档向量相似度加权求和，得到两个实例的最终相似度。通过预设的经验性阈值，过滤掉相似度低于阈值的匹配对，输出最终高于阈值的匹配对，得到最终的实例匹配结果。
3.基于聚类的分块方法
胡伟等研究人员提出了一种基于分治算法的大型本体匹配算法[122] ，该方法适合处理有大量概念和属性的知识图谱。该方法发展了一种基于结构的划分算法，其处理过程如图5-15所示，主要包括本体划分、块匹配和匹配结果发现三个过程。这个划分算法将一个本体中的概念聚类为多个小规模的簇，然后通过分配 RDF 声明的方式来构建块。来自不同知识图谱中的块根据事先计算好的锚进行相似性匹配，在这一步中，有着高相似度的映射块将会被选择。最终，虚拟文档和结构匹配两个匹配器将会从所有的映射对中找出匹配结果。
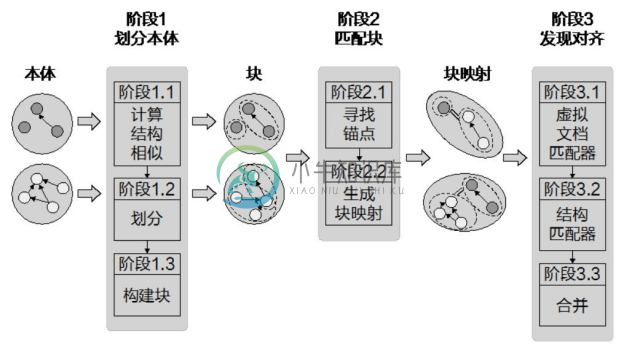
图5-15 基于聚类分块的匹配过程[122]
令O为一个本体，D为O包含的实体集合。一个D的划分称为G,G将D切分成簇的集合{g1 ,g2 ,g3 ,⋯ ,gn }。块bi 对应一个簇gi （i=1,2,3,⋯ ,n）,bi 为簇gi 包含的RDF语句的并集（bi =s1 ⋃s2 ⋃⋯⋃sm ），其中每一个sk （k=1,2,3,⋯ ,n）满足subject（sk ）∈gi ,∀bi bj ，其中i,j=1,2,⋯ ,n且 i`≠j,bi ∩bj =∅。
给定B,B′是两个分别由本体O,O′生成的块集合。将B与B′匹配将会找到一个块映射的集合BM={bm1 ,bm2 ,bm3 ,⋯,bmn }。每一个bmi （i= 1,2,⋯ ,n）是一个四元组：＜id,b,b′ ,f＞，其中 id 是一个标识符；b,,b′ 分别是B,B′ 中的两个块；f是b,b′ 的相似度，取值范围为[0,1]。
对于大型的知识图谱，该方法将概念聚类并具体化，并尽可能保证聚类的块在不同粒度下保持稳定，其聚类的依据常常为结构相似度。类间的结构相似度表示rdfs:subClassOf关系中两个实例在继承关系中的远近。若ci ,cj 是本体O中的两个类，ci ,cj 的结构相似性被定义成：
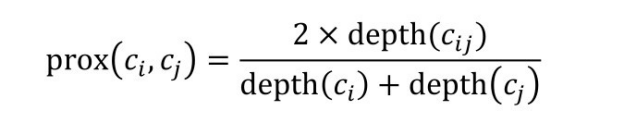
式中，cij 是ci ,cj 共同的父类；depth（ck ）为ck 在原始的继承关系中的深度。
属性的结构相似度没有类的结构相似度使用得那么频繁。属性的结构相似度不仅仅由继承关系中的距离决定，还由属性间是否有重叠的rdfs:domain（s）判定。领域的属性是为相同类别服务的，所以它们是相关的。若pi ,pj 是本体 O 中的两个属性，pi ,pj 的结构相似性被定义成：
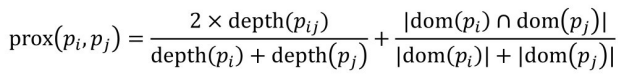
式中，pij 是pi ,pj 的共有的父属性；depth（pk ）为pk 在继承关系中的深度；dom（pk ）为pk 对应的领域信息。
在计算匹配相似度前，需要将大规模实例数据进行划分，划分的目标是将一个节点的集合划分成一个互不相交的聚合的集合g1 ,g2 ,g3 ,⋯,gm ，其中，在特定的判别方式下，聚类结果的类内节点的关联要尽可能高，同时类外节点的关联应尽可能低。基于这种思想，该方法使用了自底向上的聚合聚类算法，通过一个判别函数计算一个簇中的节点的聚合程度，以及不同簇中节点的聚合程度。给定两个簇g1 ,g2 ，两个簇中元素的结构相似度矩阵W,gi ,gj 之间的判别函数为：
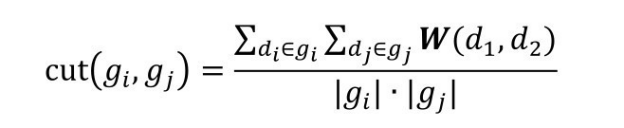
当gi ,gj 相同时，这个公式计算了簇内部的聚合性；当gi ,gj 不同时，这个公式计算了两个簇之间的聚合性。
聚类算法的具体过程为：输入是一个待聚类的集合，为每一个元素创建一个类，则每一个类的聚合度就是这个元素在继承关系中的深度。在每一次迭代中，算法选择具有最大聚合性的簇gs ，并且寻找与gs 的聚合度最大的簇gt ，当将gs ,gt 合并以后得到簇gp ，算法会根据cut（）函数重新计算gp 与其他簇之间的聚合程度，同时也会更新自身的聚合程度，当有一个簇的元素数量超过了限制或者没有聚合可以匹配的时候，聚类过程完成。
这样，一个本体中的所有实体就被划分成了一个互不相交的簇的集合。但是这些簇不能直接被用来对本体中的元素进行匹配，因为这些实体失去了 RDF 三元组的关联关系（注意上一步操作做的是一个划分，所有的簇之间都没有重合的三元组）。需要把具有关联关系的三元组还原到簇中。这里采用一种简单的方式，如果一个三元组ti 的主语和宾语都存在于一个簇gi 中，那么就把这个三元组ti 放入gi 中。但是这里的空白节点被遗漏了，需要采用了RDF语句保存更多的语义信息。
在匹配阶段，一个非常暴力的方式是依次比较本体中的两个块，但是实际上并没有必要，因为很大部分的本体之间没有匹配对应的部分。这里提出了一种启发式的算法来发现匹配的块。首先采用了一种字符匹配技术发现两个完整的本体之间的锚，之后两个本体中的块依据锚的分布被匹配起来。
最后，在匹配的块的基础上进一步计算匹配的概念对，其中采用了基于语言的匹配器V-Doc和基于结构的匹配器GMO。
实验结果表明，该方法在很多大本体上都获得了较好的匹配性能。同时需要注意到，对于包含大量实例的知识图谱，由于该方法中采用的 RDF 声明并不适用于对实例的描述，因此聚类过程需要进行相应的调整。
4.基于局部性的分块方法
汪鹏和徐宝文等研究者利用了大规模知识图谱的结构特点和匹配中的区域性特点，提出了一种无须对大规模知识图谱进行分块的知识融合方法，该方法在匹配计算中根据当前得到的匹配结果，及时预测后继相似度计算中可跳过的位置，从而达到提高映射效率的目的。该方法可同时处理知识图谱中的本体匹配和实例匹配[127] 。
大规模知识图谱融合中普遍存在两种事实：①大规模知识图谱中的本体包含大量由Is-a和Part-of关系构成的层次结构，正确的匹配不能破坏这种层次结构；②大规模知识图谱间的元素映射具有区域性特点，即知识图谱 O1 的特定区域 Di 中的元素大多会被映射到知识图谱 O 2 的特定区域 Dj 中，以块为单位的本体匹配结果也证实了该事实[128,129] 。这两种事实为寻找有效的大规模知识图谱融合方法提供了新思路。首先，由于匹配不能破坏原知识图谱的结构层次，当能够确定O1 中的概念A与 O2 中的概念 B匹配时，则A 的子概念不必再与B的父概念做匹配计算，从而能减少很多无谓的相似度计算。其次，由于匹配的元素集具有区域性，则可认为元素及其邻居通常只与另一本体中的部分元素相关，而与其他大多数元素无关。因此，当能确定A与B不匹配时，就可以认为A的邻居与B也不会匹配，这同样能避免很多无谓的相似度计算。
图 5-16（a）显示了知识图谱本体层次结构与匹配。如果在计算 ai 的相似度时，发现它与bp 或bq 具有较高的相似度，因此有理由相信：ai 与bp 或bq 匹配的可能性较大。这样带来的直接好处是：在随后的相似度计算中，可以直接跳过 ai 的子概念与 bp 或 bq 的父概念，以及 ai 的父概念与 bp 或 bq 的子概念的相似度计算。称满足这种特点的 bp 和 bq 为 ai 的正锚点。
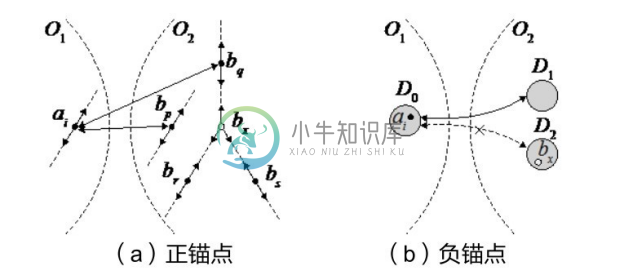
图5-16 正锚点和负锚点[131]
定义 5-19（正锚点） 给定O 1 中概念ai ，设它与O2 中的元素b1 ,b2 ,…,bn 的相似度为Si1 ,Si2 ,…,Sin ，称相似度大于阈值 ptValue 的 O 2 中的概念构成的集合为 ai 对应的正锚点（Positive Anchor），即PA(ai )={bj |Sij >ptValue}。
如果相似度是对称的，则正锚点也是对称的，即如果
，则有
。
阈值 ptValue 一般取区间[0,1]中较大的值，具体取值要根据相似度计算方法的特点确定。由于 ai 只可能与 O2 中的少数元素具有较高相似度，因此 ai 的正锚点包含的元素一般较少。
如果把知识图谱中的元素按照关联程度划分为多个区域，则观察映射结果可以发现O1 中区域 Di 的元素大多数会与 O2 中区域 Dj 内的元素匹配。基于分治思想的映射方法正是利用了匹配的区域性特点。图5-16（b）显示了知识图谱匹配的区域性特点，其中实线双箭头表示区域 D0 与 D1 中的元素匹配，虚线双箭头表示 D0 与 D2 不匹配。设 ai 和 bx 分别是 D0 和 D2 中的元素，则有理由相信 ai 和 bx 的相似度较小，由此可进一步推测 ai 的邻居与 bx 的相似度同样较小，于是在随后的相似度计算中，可以直接跳过 ai 的邻居与 bx 的相似度计算。称满足这种特点的bx 是ai 的负锚点。
定义 5-20（负锚点） 给定 O 1 中元素 ai ,O 2 中的元素 b 1 ,b 2 ,…,bn 的相似度为Si1 ,Si2 ,…,Sin ，称相似度小于阈值 ntValue 的 O 2 中的元素构成的集合为 ai 对应的负锚点（Negative Anchor），即NA(ai )={bj |Sij <ntValue}。
当相似度计算是对称时，得到的负锚点同样具有对称性。
阈值 ntValue 一般取区间[0,1]中较小的值，具体取值也要由相似度计算方法的特点确定。由于ai 可能与O2 中的大多数元素都不相关，因此ai 的负锚点包含的元素一般较多。
正锚点和负锚点提供了两种提高大规模匹配效率的手段。利用这两种锚点，相似度计算过程中可跳过大多数位置的计算，从而降低计算的时间复杂度。显然，正锚点和负锚点无法事先确定，因此需要在相似度计算中动态确定锚点，并利用得到的锚点预测后继相似度计算中那些可直接跳过的位置。下面分别给出两种基于锚点的匹配预测算法，然后再讨论综合利用两种锚点的混合算法。
当计算O1 中概念ai 与O2 中全部概念的相似度后，便可以根据ai 的正锚点预测后继匹配计算中可跳过的位置，称这种根据正锚点预测得到的匹配位置为正约简集。显然，正约简集只有在 ai 的正锚点中的概念集合不为空时才可能得到，正锚点中的概念可能不止一个，为保证正约简集中包含较多正确的可跳过位置，预测时取相似度最大的top-k个正锚点。
这里不失一般性，以图5-16（a）为例分析正约简集的构造方法。当正锚点为空时，不会得到正约简集。下面分别讨论正锚点包含一个概念和多个概念时的正约简集计算。
（1）正锚点只包含一个概念。假设PA(ai )={bp }，则根据知识图谱结构层次的特点可得到正约简集：
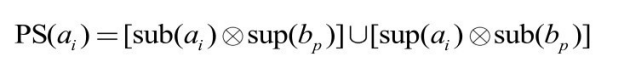
式中，sup(e)和 sub(e)分别表示 e 的父类和子类的集合。符号
表示两集合构成的元素对集，即
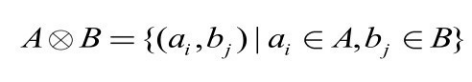
（2）正锚点包含多个概念。设 PA(ai )={bq ,br }，由于 bq 和 br 位于同一个层次结构中，令它们之间的元素集合为mid(bq ,br )。又令PS(ai |br )表示当ai 的正锚点为br 时对应正约简集，即
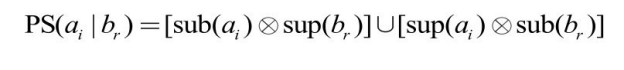
同理有：
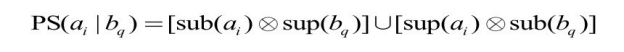
因为
和
，上面两式可进一步化为：
上面两式表示的正约简集都由三个子集合并构成，二者差别在于最后一个子集。如果取 ai 的正约简集为两式的并集，则将导致 ai 所在的层次结构中的其他元素与 mid(br ,bq )中元素的相似度计算都会被跳过，因此这样得到的正约简集包含某些不能跳过的匹配位置可能性会增大。所以，为了降低风险，此时应取两式交集作为ai 在这种情况下的正约简集，即
再假设正锚点中的多个概念互为兄弟，如 PA(ai )={br ,bs }。此时，bx 为 br 和 bs 的最小上界，设
，将bx 引入正约简集，得到如下两式：
为了避免正约简集引入过多不能跳过的匹配位置，上述两式应该取交集，也就是说上两式的集合中的后两部分都很可能预测错误的可跳过位置，于是有：
如果这里的br 和bs 有公共子类，设最大下界为mlb(br ,bs )，则上述正约简集为：
显然，之前讨论的PA(ai )={bp ,br }的正约简集计算是这种情形的一种特殊形式。
对上面的分析进行一般性推广，可以得到 PA(ai )={b 1 ,b 2 ,…,bk }时的正约简集计算公式：
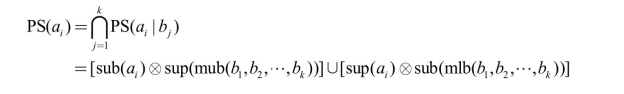
由上式可见，top-k 取值越大，得到的正约简集越小，但正约简集中引入不可跳过位置的风险也随之降低。在本文实现中，top-k的取值一般为1～4。
将 O1 的全部概念对应的正约简集合并，便得到相似度计算中总的正约简集，即基于正锚点所能预测的全部可跳过匹配位置集合：
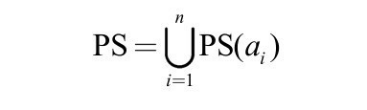
正约简集是在相似度计算过程中动态得到的，根据它对后继匹配的影响可将其中的匹配位置分为两部分：①匹配位置在之前已计算过，这类匹配位置对减少后继的相似度计算并无帮助，称为无效正约简集；②匹配位置还未被计算过，这类匹配位置可被用于跳过随后的相似度计算，称为有效正约简集。可见，有效正约简集大小才是提高相似度计算效率的因素。在匹配过程中，相似度计算的次序会影响到最终的有效正约简集大小，因此有必要讨论如何选择合理的相似度计算次序，以产生最大的有效正约简集。
为方便讨论，假设知识图谱 O1 和知识图谱 O2 相同，即对于 O1 中的任意概念 ai ,O2 中有且仅有 bi 与之匹配，也就是 PA(ai )={bi }。任选两本体对应的一条长为 L 的层次路径，对路径上的概念按层次编号为1,2,…,L。如果相似度计算的第1步选择路径两端的概念，即 s1 =1或 s1 =L 时，产生的有效正约简集大小显然为0。如果第1步选择第 k （1<k<L）个概念，得到的有效正约简集大小则为 PS=2(k－1)(L－k)。以此类推，可以看出，每次相似度计算选择的概念不同，产生的有效正约简集也可能有差别。因此，匹配顺序决定着能产生多少正约简集。
经过分析，匹配顺序与最大有效正约简集的关系可由定理5-1确定。
定理5-1 当匹配过程中选择的概念次序可将层次路径不断等分时，正锚点生成的有效正约简集最大。
证明过程在此略去。
根据定理5-1，对于完全等价的两本体中长度为 L 的路径，最优的一种匹配次序是
这些点将层次路径不断等分为
这种划分过程可以通过递归实现。
当两本体完全相等，且本体中所有概念构成一条长度为 n 且无分支的链状层次结构时，匹配过程可产生 n(n-2)大小的有效正约简集，即实际需要做匹配计算的位置个数为：n2 -n(n-2)=2n，此时算法时间复杂度最好为 O(2n)。然而，这种理想情况在实际本体匹配中几乎不存在。现实本体中的层次结构往往由多条带分枝的路径构成，假设层次结构从顶概念出发到底层孩子概念（即叶子节点）的路径共有 m 条，则路径平均长度或者说层次结构平均深度为
，如果忽略路径间的覆盖因素，所得到的最大有效正约简集平均大小为
即需要计算相似度的位置数为：
，因此匹配算法的时间复杂度为
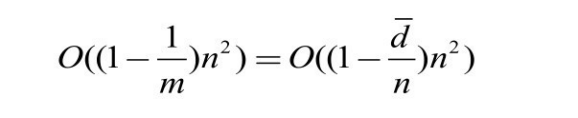
可见，只有当路径条数较少，或者层次结构平均深度较大时，才能有效提高匹配计算的效率，如果本体中的层次结构较浅，则会降低匹配算法的效果。
根据ai 的负锚点，同样可以预测后继相似度计算中可跳过的位置，称这种根据负锚点预测得到的匹配位置为负约简集。根据负锚点的定义，ai 和它的负锚点具有较低的相似度，即 ai 很可能与负锚点在语义上无关，因此可进一步推测 ai 的邻居与 ai 的负锚点同样不相关，这样 ai 的邻居在做相似度计算时可跳过 ai 的负锚点中包含的元素。这里的邻居不限于直接邻居，而包含在知识图谱中并与ai 距离为nScale的元素。
负约简集的计算方法比较简单。给定 ai 和它对应的负锚点 NA(ai )，并令与 ai 距离为nScale 的邻居集合为 Nb(ai )={ax |d(ax －ai )<=nScale}，则 ai 产生的负约简集为
。得到负约简集的同时，ai 负锚点也通过负约简集传递给它的邻居。令aj 
Nb(ai )，且aj 的相似度在ai 之后计算，当计算aj 的相似度时，所有(aj ,bx )且bx 
NA(ai )的位置都被跳过，这部分位置被视为aj 的负锚点的一部分，即
，也就是说ai 的负锚点传播给了aj 。
负锚点的无限制传播将会导致负约简集的可信度降低。在一条长度为L的概念层次路径P=(a1 ,a2 ,…,aL )上，只要nScale>0,a1 的负锚点将最终传播给aL 。考虑到a1 和aL 的距离可能较远，它们的语义关系实际可能并不密切，所以无法保证 a1 的负锚点中的元素与 aL 也无关。因此，这种无限制传播带来的风险是后继相似度计算会遗漏某些需要计算的位置，从而得到错误的匹配结果。图 5-17 可解释负锚点传播带来的风险。ai 和 aj 对应的负锚点分别为：NA(ai )=Ns +Np ,NA(aj )=Np +Nq 。NA(ai )
NA(aj )=Np ，即 Np 是二者共有的负锚点。如果aj 的相似度计算在ai 之后，对aj 来说，由于得到了 ai 的负锚点，计算相似度时将跳过 Ns ，如果正确匹配包含在 Ns 中，则该匹配结果就被遗漏了，所以传播得到的Ns 对 aj 的相似度计算是危险的。同理，如果先计算 aj ，则Nq 对ai 的相似度计算同样存在风险。
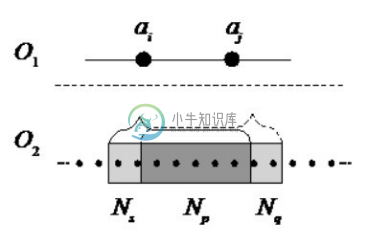
图5-17 负约简集的风险[131
为降低负锚点传播导致的风险，需要对负约简集的生成进行约束。这里采用的约束条件如下。
约束条件1： 可传播的负锚点必须是元素相似度计算中得到的，由邻居传播过来的负锚点不能再次被传播。
根据该约束条件，图5-17中aj 的负锚点包含两部分：ai 传递过来的Np 和aj 自身相似度计算中得到的 Nq 。aj 只能将 Nq 传递给随后做相似度计算的其他邻居。约束条件1有效降低了负锚点传播带来的风险，但也减小了产生的负约简集规模。
这里还采取了其他两种约束条件进一步降低负约简集的风险。
约束条件2： 负锚点能传播的邻居必须在位于ai 的语义子图内，称为SSG约束。
约束条件3： 当元素的语义描述文档包含词条数大于阈值 t 时，产生的负锚点才能传播，称为SDD约束。
约束条件2通过语义子图保证负锚点只传播与元素语义关系密切的邻居，这样得到的负约简集的可信度更大。
约束条件3并不具备通用性，而仅仅是根据本章使用的语义文本匹配器而规定的。当某些元素缺乏足够的文本信息时，它的相似度计算得到的负锚点可能是错误的，在这种情况下的负锚点不应该被传播。这里用语义描述文档中的词条数来估计元素的文本信息。本文实现中取t=8。
与正约简集生成时类似，元素相似度计算次序也将影响负约简集的大小。对于包含 n个元素的本体，元素匹配顺序有 n！种可能，为了在匹配过程中得到最大的负约简集，需列举全部 n！种可能的匹配顺序，这样的代价显然太大。设相似度计算时第 k 个元素 ak 对应的有效负约简集的大小为：
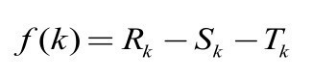
式中，Rk 表示ak 的负约简集，Sk 和Tk 均是Rk 的一部分，Sk 表示Nb(ak )中已做相似度计算的元素在 Rk 中对应的那部分负约简集；Tk 表示 Rk 中包含的之前相似度计算中已得到的负约简集。上式说明负约简集去除 Sk 和 Tk 两部分后，才是对后继匹配有益的有效负约简集。由于元素对应的负锚点大小通常差别不大，因此可视为常数 P。令 wk =|Nb(ak )|，则Rk =Pwk 。Nb(ak )中已做相似度计算的元素数目无法确定，但随着 k 的增加，元素邻居已被相似度计算过的可能性会增大，因此用 wk u(k)来估计这类元素的数目，这里的 u(k)是关于k 的单调上升函数，且0≤u(k)≤1，所以
。Tk 同样用一个关于k 的单调上升函数v(k)来估计
。这样，上式可改为：
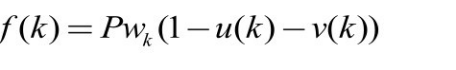
上式指出，随着 k 的增加，
会不断减小，这便意味着为了匹配过程得到的有效负约简集最大，必须在匹配早期选择 wk 较大的位置，即邻居较多的元素。在实际算法中，这里用度较大的元素近似替代邻居较多的元素。
上述这种产生最大有效负约简集的思想是贪心思想。由此得到基于负锚点预测的匹配处理过程。下面对该负锚点预测的复杂度进行分析。假设元素的邻居数目平均为 w，每个元素平均能产生的负锚点大小 P，且 P 通常与元素总数 n 成正比
，每次相似度计算时的 Sk +Tk 平均为 ε，则匹配过程得到的有效负约简集大小约为
，也就是说需要计算的匹配位置总数为：
由于ε一般不大，因此匹配算法的时间复杂度为
。显然，影响算法效率的主要因数是 w 和
，邻居平均数目 w 越大，算法越快；
越大，即负锚点平均大小 P 越大，算法也越快。w的大小除与本体结构特征有关外，还受3个约束条件的影响。决定
大小的参数主要是确定负锚点时选择的阈值ntValue。
SiGMa 匹配的思想也可以视为一种利用了局部性的实例匹配方法[130] 。在匹配开始，提供一些高质量的匹配对，然后在多次迭代过程中使用贪心策略发现更多的匹配；在迭代过程中，根据图的连通性，比较已匹配结果的邻居，从而发现更多的待匹配结果。
5.4.5 基于学习的实例匹配方法
大规模知识图谱的实例匹配可视为机器学习的一个二分类问题，因此可以利用知识图谱中丰富的网络结构信息和实例相关的信息来训练一个分类模型，从而实现实例匹配。同时，由于实例的规模较大，在分类之前需要对实例进行分块，通常采用基于属性的规则来进行分块处理。
胡伟等研究者较早采用半监督学习的自训练方法来解决实例匹配问题[131] 。近年来，知识图谱嵌入技术也被用于实例匹配中，该方法在知识图谱嵌入结果的基础上将实体匹配视为一个二分类问题，期望学习的嵌入结果具有最大的实体匹配似然[132] 。其中，该方法提出了 limit-based 目标函数，该目标函数除了可以区分正反三元组，还能控制三元组的具体得分；还提出解决训练的嵌入结果更具区分性的负例抽样方法；从全局最优的角度标记新的匹配；为了避免标记过程中的错误积累，提出了一种标签编辑方法来重标记或取消错误的新实体对齐。
在学术知识图谱中，同名的作者不是相同的人，以及同一个人的名字有多种写法，这是这类知识图谱构建中存在的一个重要挑战问题，通常称为作者指代消解问题。唐杰等研究者提出了一种基于隐马尔科夫随机场的概率框架以解决作者指代消解问题[133] ，其中定义了该问题的消解目标函数和参数估计方法。随后，表示学习等技术也由唐杰等人引入作者指代消解中[134] ，表示学习得到的向量不仅可以计算各种相似度，还可用于候选匹配集的聚类以及聚类大小的估计；此外，针对不断更新和增加的学者信息，给出了一种持续消解的解决思路。
东南大学的赵健宇和汪鹏等人针对学术知识图谱中的作者指代消解问题，提出了一种半监督的作者指代消解方法[135,136] 。根据学术知识图谱的特点，该方法的解决思路主要关注数据集中三个方面的信息：基于作者发表文献的主题、年份、关键字和个人信息等特征构造的相似度信息；基于给定作者的合作者以及合作者的主题构造的合作网络的相似度信息；数据集中判断两个作者名是否需要消解的判断规则。该方法的技术路线如图5-18所示。其中，输入数据为学术知识图谱，包含学者、论文、学者合作信息和论文基本信息等；消解后的作者聚类为输出。该方法的指代消解技术路线分两大块，步骤①～⑤是基于无监督算法的指代消解，主要采用消解判定规则、主题特征和社交网络特征等信息通过聚类进行指代消解；步骤⑥、⑦步基于无监督算法的指代消解结果，通过离群点消除降噪生成训练数据并训练 SVM 分类器，完成监督学习的指代消解，并最终将两个阶段的消解结果合并作为整个技术路线的指代消解结果输出。该方法使用的技术路线能够很好地完成无标注指代消解数据集的消解任务。通过无监督算法产生可靠的标注，利用半监督学习的思想在数据集中传递标签，很好地解决了无标注数据集的冷启动（Cold Start）问题。上述7个处理步骤的描述如下。
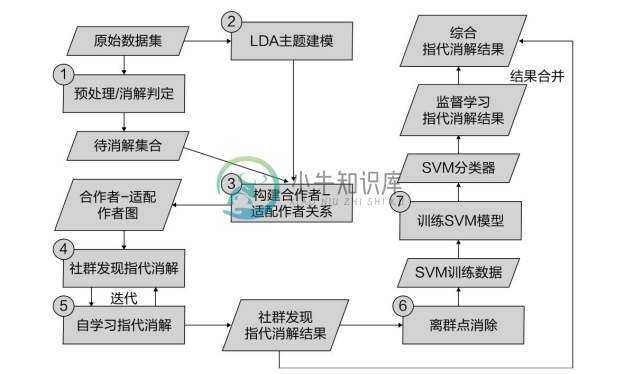
图5-18 半监督作者指代消解技术路线
步骤①。 基于作者和文献信息计算出签名频率、活跃年份等统计量，并根据消解判定规则分离需要进行命名消解的数据。
实际的指代消解过程往往需要处理大量的作者名数据，因此对作者名两两对比进行消解的代价十分高昂。因此，有必要给定一系列消解判定规则，既能够直接排除不需要消解的作者名对以提高消解效率，又能够照顾“同名异体”和“异体同名”问题，使得需要消解的作者名对能够进入消解过程。可能对应统一实体的两个作者名是“适配”的，系统将消解所有适配的名字对，并跳过不适配的名字对，以减少指代消解的计算量。
对于任意作者名，其名字的首字母和姓氏中长度为4的子串的组合被称为该作者名的签名形式。如“Chen Chen”与“Anoop Kumar”的签名形式分别为“C Chen”和“A Kumar”。对于属于同一实体的两个作者名，他们的签名形式必然相同。根据作者的签名形式可以将名字集合划分为多个集合，从而减少了指代消解过程的计算量，并可以通过多线程并行的方法增加指代消解系统的吞吐量。但是，对于签名形式相同的两个作者，很可能因为名字数据的缺失和研究方向的相似性而造成错误合并，因此还需要进一步优化消解判定规则。
对于“多义词”问题，即同名的作者数据实际对应着不同的作者，导致这种问题的原因主要有：常用名和高频姓氏的组合，如“Adam Smith”和“Mohammed Khan”等；多音字语言的英文写法冲突，如“Chen Chen”可能对应着“陈辰”和“陈晨”；缩写映射冲突，如“Anoop Kumar”和“Adam Kumar”都可能被简写为“A Kumar”。
根据上述分析，可以得到针对“多义词”问题相关的消解判定规则如下。
规则1（高频签名形式规则）： 对于签名频数超过阈值 T1的两个作者名，标记为 D1型适配；
规则2（拼音规则）： 对于汉语、粤语和韩语等语言的两个作者名，且满足签名形式相同，标记为D2型适配。
对于“同义词”问题，即单一作者的名字在文献和数据库中以不同的形式出现，导致这种问题的主要原因有：中间名缩写规则不同，如“Michael O J Thompson”可能被缩写为“M Thompson”和“Michael Thompson”；数据识别与收集的噪声，部分通过OCR识别的数据可能将“m”识别为“nn”,“i”识别为“l”;Unicode 兼容性噪声，一些数据库会将西文字符转换为相似的英文字符，如“ö”转换为“o”,“é”转换为“e”。
根据上述分析，可以得到针对“同义词”问题相关的消解判定规则如下。
规则3（签名形式规则）： 对于两个满足适配必要条件的作者名，若其中一个名字的完全形式与签名形式相同，标记为D3型适配；
规则4（编辑距离规则）： 对于满足适配必要条件的两个作者名，且任一名字的完全v姓氏不为签名形式，且名字和姓氏的拼接串编辑距离大于或等于T2，则标记为D4型适配；
规则5（中间名匹配规则）： 对于满足适配必要条件的两个作者名，若一个作者的中间名缩写串不为另外一个名字中间名缩写串的子串，反之亦然，则标记为不适配；
规则6（中间名缺失规则）： 对于满足适配必要条件的两个作者名，若一个作者名的中间名缩写串为空，且另外一个作者名为签名形式，则标记为D5型适配；
规则7（活跃年份规则）： 对于签名形式相同，且活跃年份相似度小于阈值T3的两个作者名，标记为D6型适配；
规则8（普通规则）： 对于签名形式相同，且不满足上述适配型的作者名字对，标记为D7型适配。
根据上述消解判定规则，可以将知识图谱中的学者分成多个更小的部分，以提高指代消解的效率。
步骤②。 基于作者人工确认的文献数据集利用LDA模型建立作者—主题分布特征。
针对作者指代消解问题，使用的LDA和Gibbs Sampling方法对每个作者发表的文献进行主题建模，以得到作者—主题分布及主题—词汇分布。
在学术知识图谱中，每条文献记录可能但不全含有标题、出版年份、发表地、作者信息及关键字，每条作者记录对应多条文献记录。因此，该方法将每个作者对应文献中的标题、发表地及关键字信息按照空格分词，看成一个文档，并使用作者记录在数据库中的编号唯一标识该文档。
通过 LDA 主题建模，将每个作者的文献信息映射为潜在主题分布所表示的主题向量。通过主题向量可以了解作者的研究领域信息，并对不同作者的领域相似度做比较。使用 LDA 进行主题建模具有以下优点：LDA 在词包（Bag-of-Words）假设下可以统计出词汇间的相关性，从而可以使用文献丰富作者的主题特征推测文献较少作者的主题特征；通过 LDA 对词汇进行主题聚类，可以将作者的文献信息表示为更方便计算和存储的主题向量，避免了使用词汇表向量所造成的空间复杂度和稀疏问题。
在后文提到的基于社交网络社群发现的指代消解算法中，可以发现使用 LDA 主题特征在消解效果上优于使用TF-IDF权重向量。
步骤③。 结合作者人工确认的作者-文献关系及步骤①、②中的统计量和主题特征建立合作者关系图，并使用社群发现算法完成第一次指代消解。
给定学术知识图谱可以构建合作者-适配网络，用于描述作者之间共同发表文献的合作关系及潜在的消解关系，能够对挖掘作者的领域特征和合作特征提供良好的基础，并能够直接用于指代消解。
基于合作者—适配作者网络可视化的数据分析，可以做出一个假设：对应同一实体的作者，其对应的顶点拥有较高权重的适配边和一定数量的合作者边，属于同一合作者“圈子”。在社交网络分析问题中，社群发现算法是一种将网络分解为多个子网络的方法，每个子网络都在对应的相似度度量下具备高内聚特性。网络的内聚特性由模块化度（Modularity）衡量，给定一个网络G及其顶点集划分，可定义其模块化度。
这里使用快速展开社群发现算法[137] 处理在上一节中构建的合作者—适配作者网络。算法包含两个阶段。第一个阶段遍历每个顶点，并将该顶点临时修改为邻接顶点的社群编号，计算模块化度增量，使用非负增量的修改作为最终修改，不断执行上述步骤直至模块化度收敛。第一阶段结束后，将社群编号相同的顶点合并为同一顶点，在新顶点组成的网络中，边的权重由社群间的边权重之和计算而得。
步骤④。 在第一次指代消解的基础上，合并已消解的作者，重复步骤③直至作者消解结果无变化，从而得到第二次消解结果。
由于整个知识图谱中的所有作者都需要进行指代消解，因此合作者也存在指代消解问题。也就是说，在基于原始数据构造的合作者-适配作者网络中，可能因为合作者未消解而造成共享合作者顶点的缺失，即合作者边的缺失。如果两个适配作者的主题相似度较低（往往是由于研究方向变化造成的），又缺乏合作者边的信息补充，则基于原合作者—适配作者网络的指代消解结果的召回率会降低。因此，本方法使用自学习的指代消解进一步处理第一次指代消解结果。
由于自学习指代消解需要使用上一次指代消解的结果，因此需要能够保存并快速查询给定的两个作者名是否已经合并，以及给定作者名已消解的其他作者名。该方法使用并查集实现。给定一个作者，通过并查集找到与之相同的其他作者，并使用编号最小的作者名代表整个作者集合，称为代表作者。代表作者的合作者是所有已消解作者的合作者的并集。在新的合作者-适配作者网络中，两个代表作者边的权重由各自消解集合中最大的主题相似度确定。
对新的合作者-适配作者网络，使用上一节描述的社群发现算法，对每一个社群中适配的两个作者进行合并。在合并的基础上，继续进行自学习指代消解，直至没有作者再被合并。
步骤⑤ 首先利用文献信息中的作者名调整对应作者的名字信息，结合第二次指代消解结果生成以文献对为数据的训练数据集；然后根据不同特征组合分离上述数据集，并使用SVM分别训练分类模型。
该方法使用 LibSVM[138] 训练支持向量机模型，除了对SVM模型的实现，LibSVM还提供了方便的交叉验证和参数选择工具。使用3折的交叉验证，即用70%的训练数据进行模型训练，30%的数据用于模型验证。
要使用监督学习的方法完成作者指代消解，必须要有训练数据。原始数据集中没有显式地提供任何与作者实体相关的数量和特征信息，因此无法直接根据原始数据生成 SVM所需的训练数据。但由于第一次指代消解结果已经能够达到很好的F值，因此可以根据该结果生成训练数据。虽然这种做法会对模型的训练引入一定噪声，但通过消除离群点、选择合适的参数以及交叉验证可以削弱噪声对泛化能力的影响。
根据数据中的Author、PaperAuthor、TrainDeleted、Paper、Conference和Journal关系做联合查询，可得到和作者相关的文献详细数据。文献的详细数据包括论文标题、作者所属组织、出版日期、关键词、会议名、会议名缩写、期刊名和期刊名缩写，其中某些列的值可能为空（数据缺失）。将同一 ID 作者的文献按照相同列的方式合并形成作者文献档案，如将所有论文标题在去除停止词和词干处理后用空格衔接，作为该作者文献档案标题列的值。将正例和反例的文献档案两两对比，可形成基于文献档案相似度的特征向量，向量长度和文献档案的列数量相同。
由于第一次指代消解的结果也是由指代消解的传递性生成的，因此并非任意两个文献档案的相似度特征向量都具备很典型的正例特征。为了保证 SVM 的泛化能力，需要移除这些离群点。本文采用局部离群因子（Local Outlier Factor）[139] 度量训练集中各数据的离群程度，并根据离群程度移除离群点。
步骤⑥。 使用 SVM 分类模型对潜在需要消解作者的文献集合生成文献档案并进行分类，通过分类结果完成第三次指代消解。
通过使用高质量的初始消解结果生成训练数据，可将第二次指代消解变为一个监督学习问题。给定训练数据和参数调优后的分类器，基于支持向量机的作者指代消解过程描述的算法针对每一对需要进行命名消解的作者对进行 SVM 模型预测，并根据预测结果输出该作者对是否为同一实体。算法的时间复杂度取决于需要消解的作者对，如果假设有 N对作者需要消解，该算法的复杂度为 O(N)。在实际的消解过程中，由于某一些名字变化造成更大的消解不确定性，因此对于不同的适配类型使用不同的特征组合模型。
步骤⑦。 合并第二次和第三次指代消解结果，最终生成已消解的作者聚类输出。
根据上述方法实现的大规模作者指代消解方法已在多个学术知识图谱中得到应用，公开的实验结果表明，该技术路线能获得优秀的指代消解结果，并具有较高的消解效率，大幅降低了人工指代消解的工作量。
5.4.6 实例匹配中的分布式并行处理
在前面的分析中，可以看到影响实例匹配性能的一个瓶颈是对匹配的计算。随着多线程处理器和分布式计算平台的普及，通过多线程和分布式并发的方法也可以有效提高实例匹配的处理效率。
胡伟和瞿裕忠等研究者较早采用了分布式方法来处理大规模的实例匹配[140] ，在典型的匹配过程中，大量的匹配时间消耗在虚拟文档构造、获取邻居的信息、计算相似度等过程中，通过借助 MapReduce 方法，将这些耗时的处理过程变为并行的处理，有效提高了实例匹配的效率。对于分块的方法，分块过程和分块后的匹配计算都是实例匹配的性能瓶颈，这些过程都同样可以解决分布式计算进行并行处理[141] 。
总体而言，分布式并行处理的方法是通过借助硬件计算资源来提升实例匹配的性能，性能的提升和投入的硬件成本是线性正比的。