graph/path-with-maximum-probability

Path with Maximum Probability

描述

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

Example 1:

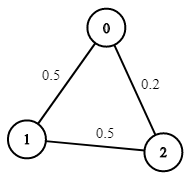
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2:

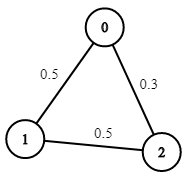
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

Example 3:

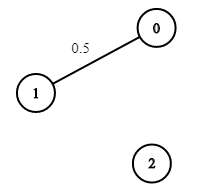
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.

Constraints:

• $2 <= n <= 10^4$
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= $2*10^4$
• 0 <= succProb[i] <= 1
• There is at most one edge between every two nodes.

分析

由于每条边的概率是介于[0,1]之间的正数，且路径上的概率是累乘起来的，那么对原图G中的每条边的权重取对数然后取反，就得到了一个边权在$[0, \infty)$之间的图G'，图G中“从起点到终点成功概率最大”的路径对应了图G'中“从起点到终点边权之和最小”的路径。由于图G'中没有负数边权，用 Dijkstra 算法最合适不过了。

代码

// Path with Maximum Probability
// Dijkstra
// Time Complexity: O(ElogN), Space Complexity: O(N + E)
class Solution {
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        // adjacency list, map<vertex_id, map<vertex_id, weight>>
        Map<Integer, Map<Integer, Double>> graph = new HashMap<>();
        for (int i = 0; i < edges.length; i++) {
            int[] edge = edges[i];
            double w = -Math.log(succProb[i]);
            // Undirected
            graph.putIfAbsent(edge[0], new HashMap<>());
            graph.get(edge[0]).put(edge[1], w);
            graph.putIfAbsent(edge[1], new HashMap<>());
            graph.get(edge[1]).put(edge[0], w);
        }

        Map<Integer, Double> dist = dijkstra(graph, start);

        return dist.containsKey(end) ? Math.exp(-dist.get(end)) : 0;
    }

    /** Standard Dijkstra algorithm.
     *
     @param graph Adjacency list, map<vertex_id, map<vertex_id, weight>>.
     @param start The starting vertex ID.
     @return dist, map<vertex_id, distance>.
     */
    private static Map<Integer, Double> dijkstra(Map<Integer, Map<Integer, Double>> graph, int start) {
        // map<vertex_id, distance>
        Map<Integer, Double> dist = new HashMap<>();
        // vertex_id -> father_vertex_id
        Map<Integer, Integer> father = new HashMap<>();

        // pair<distance, vertex_id>, min heap, sorted by distance from start to vertex_id
        Queue<Pair<Double, Integer>> pq = new PriorityQueue<>((a, b) -> Double.compare(a.getKey(), b.getKey()));

        // from start to start itself
        pq.offer(new Pair(0.0, start));
        dist.put(start, 0.0);

        while(!pq.isEmpty()){
            final int u = pq.poll().getValue();
            if (!graph.containsKey(u)) continue; // leaf node

            for(int v : graph.get(u).keySet()){
                final double w = graph.get(u).get(v);
                if (!dist.containsKey(v) || dist.get(u)+ w < dist.get(v)) {
                    final double shorter = dist.get(u)+ w;
                    dist.put(v, shorter);
                    father.put(v, u);
                    pq.offer(new Pair(shorter, v));
                }
            }
        }

        return dist;
    }
}

// TODO

相关题目

• Network Delay Time